Sahil Patel Week 12

Purpose

The purpose of this assignment is to interpret the figures and data tables in the Tai et al. paper as well as creating simulations in MATLAB.

Methods

Developing a Yeast-in-the-Chemostat Model

Convert residual glucose and residual ammonia from mM to grams.
Answer protocol questions

Develop a simulation model for a 2-nutrient chemostat.

Modify the MATLAB files chemostat_script.m and chemostat_dynamics.m to simulate a 2-nutrient chemostat
Use what parameters you have determined from the data to simulate the system.
Answer protocol questions

Results

Protocol Questions

The yield quantity Y Glu/X: this is a ratio of what quantities? Be specific and relate to the 2-nutrient chemostat model from class.
- Y(Glu/X) = ratio of Biomass produced/ Glucose consumed
The flux qGlu is a ratio of what quantities? Be specific and relate to the 2-nutrient chemostat model from class.
- flux qGlu = ratio of specific growth rate/ yield quantity
Convert residual glucose and residual ammonia from mM to grams.
- residual glucose = 0.180156 g of glucose
- residual ammonia = 0.017031 g of ammonia
Determine the length of time the chemostat is operated before data is collected.
- 1/0.03 = 33.3333 * 3 = 100 ---> around 100 hours to reach steady state.
Determine as many model parameters as you can from these data: use the "warm" data and both glucose- and ammonium-limited data.
- r = maximum rate of growth
- q = dilution rate
- K = substrate concentration (glucose) at r/2
- L = substrate concentration (ammonium) at r/2
- E = Efficiency (glucose)
- F = Efficiency (ammonium)
- u = feed concentration (glucose)
- v = feed concentration (ammonium)

MATLAB

MATLAB code

Graphs Made in MATLAB

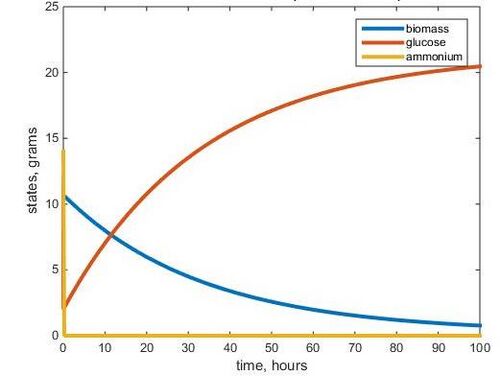
Figure 1. Graph made in MATLAB modeling warm glucose 2-Nutrient chemostat simulation using F= 1/0.05 and parameters listed above.

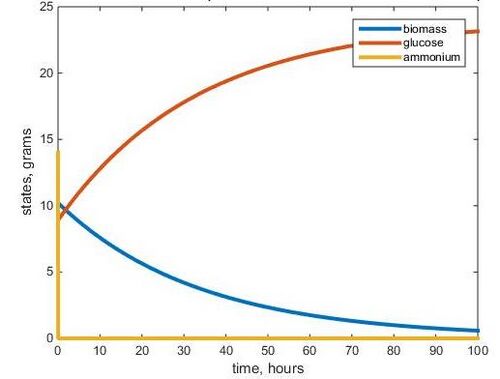
Figure 2. Graph made in MATLAB modeling warm glucose 2-Nutrient chemostat simulation using F= 64.64 and parameters listed above.

Conclusion

Using parameters from the data in the Tai et al. (2007) paper, we were able to use MATLAB to model a 2-nutrient chemostat experiment. The two nutrients used were glucose and ammonium. By comparing the glucose limited and ammonium limited chemostat environments, we can see how limiting one nutrient affects the overall growth of the population of yeast. The models allowed us to compare steady states of each nutrient and biomass and graphs were created for the 30 degrees Celsius data.

Acknowledgments

I would like to thank my homework partner Desiree Gonzalez. We met up before class on Tuesday, April 23 to work on the assignment together and so we could use each other as a resource for any questions we may have.