EdwardRyanTalatala Week 14/15

From OpenWetWare
Jump to navigationJump to search

Purpose

The purpose of this assignment was use MATLAB models to improve our understanding of the experiment and analysis of the Tai et al. (2007) paper. We also investigated the glucose efficiency/waste constant for glucose-limited and ammonium-limited conditions.

Methods

Use the MATLAB files from Dr. Fitzpatrick (zipped package).


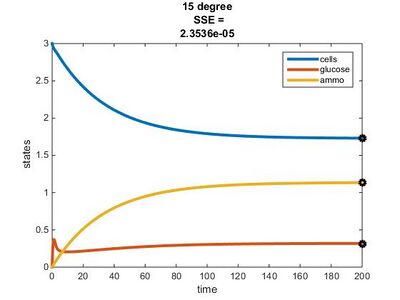
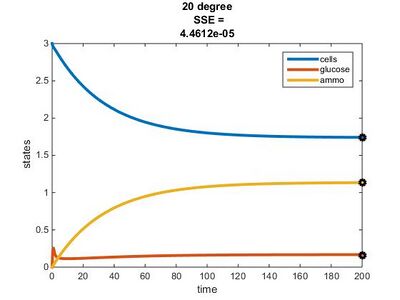
Determining temperature dependence using Arrhenius equation

Arrhenius equation: rate = A*e^(-B/(R*T))

  • Figure out the constants A and B from the rate data in the TaiParamsRevised.m file.
  • Simulate the chemostat for T = 15,20, 25 °C conditions and graph the time courses of the biomass and nutrients.

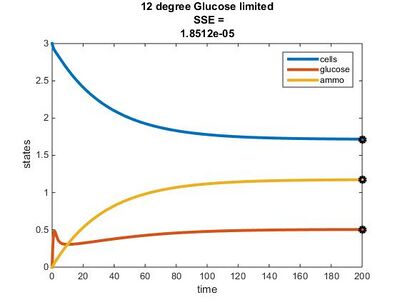
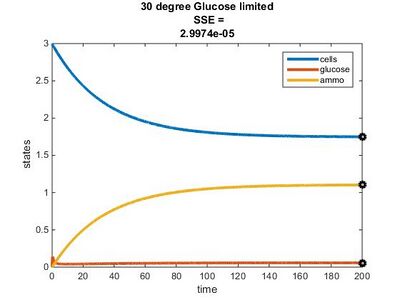
Investigating glucose efficiency/waste constant

Investigate the glucose efficiency/waste constant (that is not really a constant?) for the glucose-limited and ammonium-limited conditions.

  • Note the values of E for glucose-limited and ammonium-limited conditions.
  • For each temperature (12, 30), find a function E(y) that matches the two points of (y,E) data.
  • Modify the chemostat_2nutrient_dynamics.m file to use the functions you've created.
  • Compare the resulting simulation to the previous one.

Results

FINAL PROJECT PRESENTATION

Determining A & B Constants

Variables calculated using Arrhenius equation:

B = 69,840.59

  • found using B = (Rln(k1/k2))/(1/T1-1/T2)

A = 4.979 * 10^11

  • found by plugging in all the variables in Arrhenius equation

r(15°C) = (4.979 x 10^11)e^(-69840.59)/((8.314)(288.15)) = 0.1087

r(20°C) = (4.979 x 10^11)e^(-69840.59)/((8.314)(293.15)) = 0.1787

r(25°C) = (4.979 x 10^11)e^(-69840.59)/((8.314)(298.15)) = 0.289



MATLAB files for temperature dependence

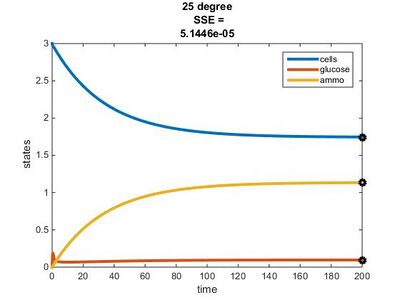
Temperature Dependence Graphs

We used the glucose-limited conditions for the 15, 20, & 25°C graphs. We changed the values for the residual concentrations in the Params file until the SSE value was close to 0.


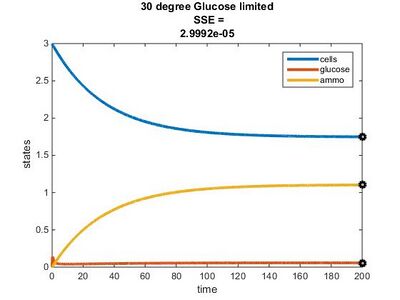
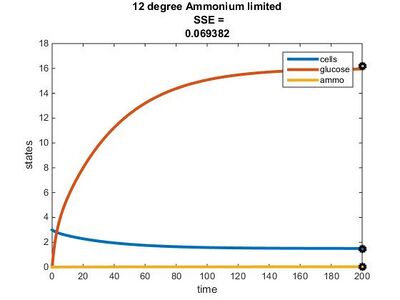
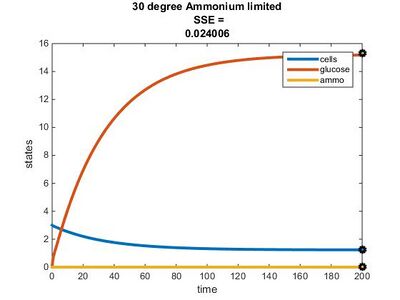
Efficiency Constant Investigation

Original: E = 1/Y

New equation: where E = my + b

  • y = residual glucose
  • use point intercept m = (y-y)/(x-x) to determine m
  • plug new value into E = my + b to determine b

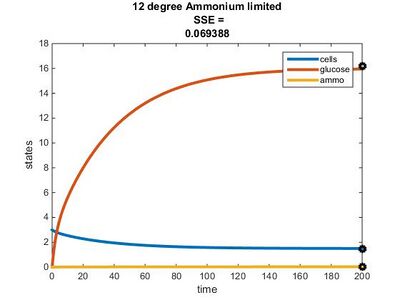
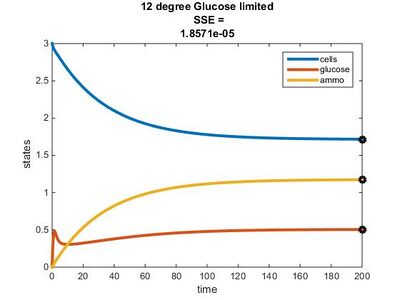
12°C: E = 0.363y + 14.11

  • m = (14.3-20)/(0.5045-16.22) = 0.363
  • b=14.11

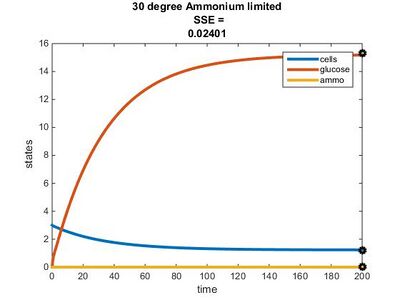
30°C: E = 0.7y + 14.25

  • m = (14.3-25)/(.0541-15.33) = 0.7
  • b=14.25

Efficiency Constant Graphs

Original Model

New Model

MATLAB files for efficiency investigation

Acknowledgments

I would like to acknowledge my homework partner, Fatimah with whom I worked with to complete the assignment.

I worked with Austin to work on the efficiency constant investigation.

Except for what is noted above, this individual journal entry was completed by me and not copied from another source. EdwardRyanTalatala (talk) 00:44, 9 May 2019 (PDT)

References

Dahlquist, K. and Fitzpatrick, B. (2019). BIOL388/S19:Week 14/15. [online] openwetware.org. Available at:Week 14/15 Assignment Page [Accessed May 8 2019].

Tai, S. L., Boer, V. M., Daran-Lapujade, P., Walsh, M. C., de Winde, J. H., Daran, J. M., and Pronk, J. T. (2005). Two-dimensional transcriptome analysis in chemostat cultures: combinatorial effects of oxygen availability and macro- nutrient limitation in Saccharomyces cerevisiae. J. Biol. Chem. 280, 437–447.

Tai, S. L., Daran-Lapujade, P., Walsh, M. C., Pronk, J. T., & Daran, J. M. (2007). Acclimation of Saccharomyces cerevisiae to low temperature: a chemostat-based transcriptome analysis. Molecular Biology of the Cell, 18(12), 5100-5112. DOI: 10.1091/mbc.e07-02-0131


Template:EdwardRyanTalatala

User:EdwardRyanTalatala


Assignments

Journal Entries


Class Journal Entries

Retrieved from "https://openwetware.org/mediawiki/index.php?title=EdwardRyanTalatala_Week_14/15&oldid=1067113"