EdwardRyanTalatala Week 11
Purpose
The purpose of this assignment was to use MATLAB to simulate differential equations that represents a chemostat, then to make a graphical representation of the results.
Methods
Population/Nutrient Chemostat Modeling
Use the MATLAB files chemostat_script.m and chemostat_dynamics.m to simulate a chemostat and compare the computations to a steady state outcome using codes in this zipfile
- Use the parameter values q = 0.10 (1/hr), u = 5 (g/L), E=1.5, r=0.8 (1/hr), K = 8 (g).
- Using the formulae, find the steady states of cell biomass and nutrient mass.
- Nutrient mass: y = (qK)/(r-q)
- Cell biomass: x = (u-y)/E
- Find the steady state concentrations of cells and nutrient assuming a 2 liter chemostat.
- Use the MATLAB files to simulate the system dynamics the parameters of (1).
- Do the graphs show the system going to steady state?
- Do the steady states match your (2) calculations?
Results
Steady states:
- nutrient mass = y=(0.1(8))/(0.8-0.1)= 1.14 g
- cell biomass = x=(5-1.14)/1.5 = 2.6 g
2 liter chemostat steady state concentrations:
- [nutrient] = 1.14g/2L = 0.57 g/L
- [cell] = 2.6g/L = 1.3 g/L
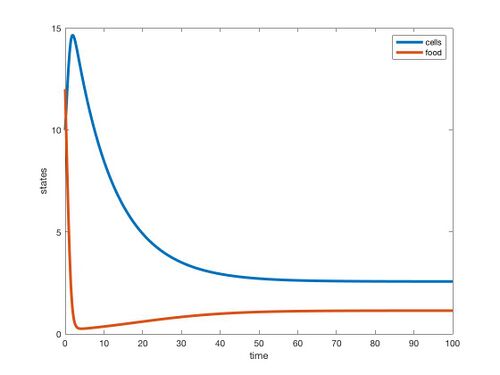
Graph from the MATLAB
Conclusion
The equations to determine the steady states of cell biomass and nutrient mass matched with the MATLAB simulation. The graph also shows that they reach equilibrium around 50 minutes. These show that changing the parameters would consequently change the steady states of nutrient mass and cell biomass, showing the MATLAB script works to represent the chemostat.
Acknowledgments
- I would like to acknowledge my homework partner, Ava with whom I worked with to complete the assignment.
Except for what is noted above, this individual journal entry was completed by me and not copied from another source.
EdwardRyanTalatala (talk) 18:39, 9 April 2019 (PDT)
References
Dahlquist, K. and Fitzpatrick, B. (2019). BIOL388/S19:Week 11. [online] openwetware.org. Available at:Week 11 Assignment Page [Accessed 9 Apr. 2019].
Assignments
- Assignment-Week 1
- Assignment-Week 2
- Assignment-Week 3
- Assignment-Week 4
- Assignment-Week 5
- Assignment-Week 6
- Assignment-Week 7
- Assignment-Week 9
- Assignment-Week 10
- Assignment-Week 11
- Assignment-Week 12
- Assignment-Week 14/15
Journal Entries
- Journal-Week 2
- Journal-Week 3
- Journal-Week 4/5
- Journal-Week 6
- Journal-Week 7
- Journal-Week 9
- Journal-Week 10
- Journal-Week 11
- Journal-Week 12
- Journal-Week 14/15
Class Journal Entries