Leanne Kuwahara-Week 11

From OpenWetWare
Jump to navigationJump to search

Purpose

To simulate a chemostat using MATLAB and compare the results to a steady state outcome.

Background

  • Chemostat: a reactor used for growing cell cultures
    • Nutrients (media) added at a constant inflow rate
    • Nutrients held at fixed concentrations
    • Effluent removed at a rate equivalent to the inflow rate
    • Effluent concentration DEPENDS on time
    • Volume in chemostat held constant
  • Assumed that contents of chemostat are well mixed (uniform concentration throught reactor)
    • Thus, all cells have EQUAL access to nutrients
  • Parameters:
    • Q: volumetric inflow rate (vol/time)
    • V: volume in chemostat (vol units)
    • q = Q/V: dilution rate (1/time)
    • u: feed concentration (concentration units)
    • y(t): concentration of nutrients
      • Rate of change of nutrients = inflow rate - outflow rate - rate consumed in tank
  • Modeling Conservation of Nutrient Mass (dy/dt):
    • qu: inflow rate (assumed to be CONSTANT over time)
    • qy(t): outflow rate
    • Er(y/K + y)x(t): consumption rate/rate of metabolism
      • Michaelis-Menten model
    • x: concentration of yeast cells
    • E: unit conversion rate between biomass and nutrient concentration
    • r: Maximum rate of system (Max specific growth rate)
    • K: Nutrient concentration at which the reaction rate is half of Vmax (r)
  • Modeling Cell Population (dx/dt):
    • Net growth rate is dependent on nutrient level [y(t)]
      • Consumption model depends on size of population
  • In EQUILIBRIUM, models are set equal to ZERO
    • x CANNOT be 0 (as this would mean the cell population was extinct)
      • Nutrient concentration at equilibrium: y = qK/(r-q)
      • Cell concentration at equilibrium: x = (u-y)/E
    • The steady-state nutrient concentration is INDEPENDENT of the feed rate (u), while the cell population DEPENDS LINEARLY on u

Protocol

  1. Solving for steady-state cell biomass (x) and nutrient mass (y):
    • Parameters used:
      • q = 0.10 (1/hr)
      • u = 5 (g/L)
      • E = 1.5
      • r = 0.8 (1/hr)
      • K = 8 (g)
        • Parameters were plugged into y = qK/(r-q) and x = (u-y)/E to solve for cell biomass and nutrient mass (g) at equilibrium
  2. The mass calculated in number 1 were divided by 2 (L) to obtain the steady-state concentration (g/L) of cells and nutrients
  3. MATLAB files chemostat_script.m and chemostat_dynamics.m were used to simulate the system dynamics
    • Same parameters were used in simulation
      • Results from simulation were compared to the calculated values
  4. Adding a Second Y-axis
    • yyaxis left/right did not work
      • Do no think this function is compatible with the 2014 version of MATLAB as it was released in 2016
    • plotyy function did not work
      • Over-layed a second y and x-axis
    • plot2axes function did not work
      • gave an error

Results

  1. Calculated cell and nutrient mass:
    • Cell biomass = 2.6g
    • Nutrient mass = 1.1g
  2. Concentration in a 2L chemostat:
    • [cells] = 1.5g/L
    • [nutrients] = 0.5g/L
  3. MATLAB simulation

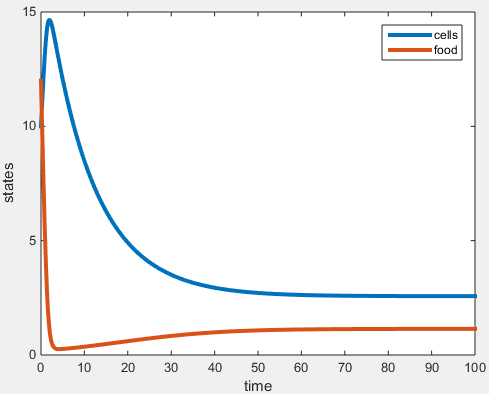
Figure 1. Plot generated in MATLAB simulation of a chemostat experiment.

  • Plot demonstrates the chemostat goes to equilibrium around 50hr
  • Plot shows equilibrium masses consistent with the calculated values (cells ~ 3g, nutrients ~ 1g)

Questions(Points of Confusion:

  • I do not understand what in the code is assigned to the y-axis and what is assigned to the x-axis
  • what are the units?? hours and g/L???

Data and Files

Chemostat MATLAB files

Conclusion

This aim of this experiment was to simulate a chemostat using MATLAB. The program produced a plot that successfully went to equilibrium, as expected with a chemostat experiment. Initially the cell population dramatically increased as the nutrient supply decreased. Once the nutrient concentration was near zero, the cell population peaked, and then decreased to a stead state around 3g. As the cell population decreased, nutrient concentration began to increase and also reached a steady state around 1g. These results demonstrate that MATLAB can be used to simulate chemostat experiments.

Acknowledgements

Except for what is noted above, this individual journal entry was completed by me and not copied from another source.

References

  • Dahlquist, K. & Fitpatrick, B. (2019). "BIOL388/S19: Week 11" Biomathematical Modeling, Loyola Marymount University. Accessed from:Week 11 Assignment Page

Links

Retrieved from "https://openwetware.org/mediawiki/index.php?title=Leanne_Kuwahara-Week_11&oldid=1064799"