Angela C Abarquez Week 15

Purpose

The purpose is to use MATLAB to create models of the temperature dependence of the chemostat reaction demonstrated in the Tai et al. (2007) paper. Additionally the glucose efficiency constant was further investigated and modified to account for the differing metabolization processes that yeast undergo under different conditions.

Methods

The MATLAB files provided by Dr. Fitzpatrick linked (here) were used.

Modeling Temperature Dependence

The Arrhenius equation (rate = A*e^(-B/(R*T)) was used on each of the four cases (glucose-limited and ammonium-limited for 12 and 30 degrees C) to solve for A and B.
The r and T values were taken from the "taiParamsRevised" MATLAB file and input into the equation, along with the universal gas constant R, to solve for A and B.
The rates for then found for T = 15, 20, and 25 degrees C.
The chemostat was then simulated for T = 15, 20, and 25 degrees C conditions. The time courses of the biomass and nutrients were graphed.

Investigating the Efficiency 'Constant'

The y and E values were taken from the "taiParamsRevised" MATLAB file for all four cases.
Using the point-slope and slope-intercept formulas, an equation for each temperature E(y) was created to relate the two points, (y,E).
The "chemostat_2nutrient_dynamics.m" file was modified to use the two developed equations.
Results were compared to the previous ones.

Results

Variables found in "taiParamsRevised" file:

12 degree C Glucose-Limited:

r=0.08
T=285.15K
y=0.504504
E=14.2857

30 degree C Glucose-Limited:

r=0.46
T=303.15K
y=0.054054
E=14.2857

12 degree C Ammonium-Limited:

r=0.08
T=285.15K
y=16.2162
E=20.0000

30 degree C Ammonium-Limited:

r=0.46
T=303.15K
y=15.3333
E=25.0000

Variables calculated using Arrhenius equation:

A = 4.979 * 10^11

B = 69,840.58946

r(15 degrees C) = 0.1087

r(20 degrees C) = 0.1787

r(25 degrees C) = 0.289

Equations developed using point-slope and slope-intercept formulas:

12 degree C: E = 0.3637y + 14.1022

30 degree C: E = 0.7012y + 14.2483

Figures

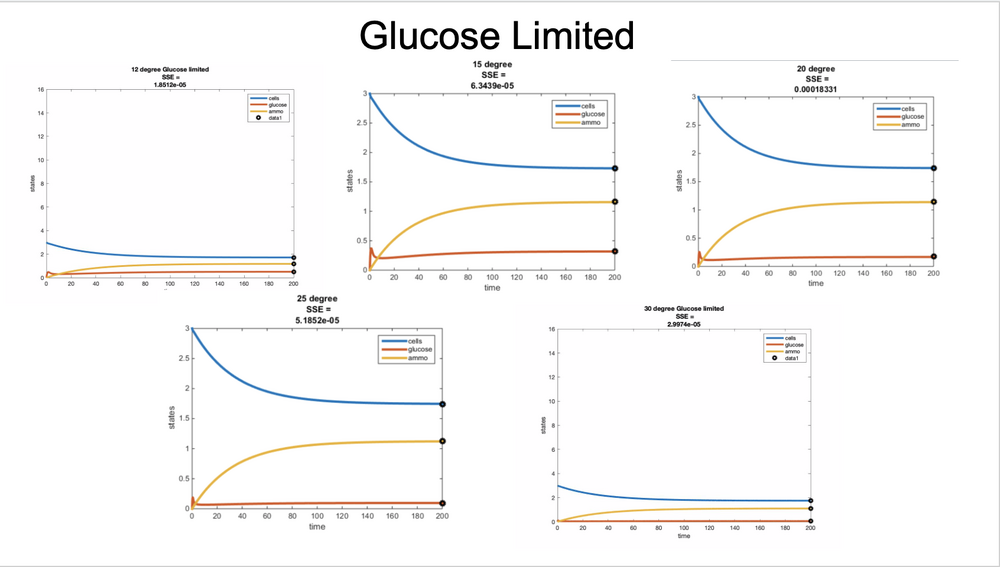Figure 1. Part 1 graphs. The Glucose-limited condition was used.

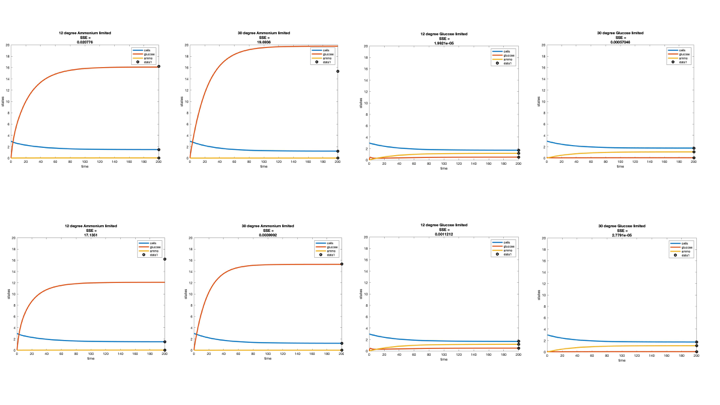Figure 2. Part 2 graphs. The 12°C equation was used for the top row and the 30°C for the bottom row.

Presentation: File:Biomathmatical Modeling Final Presentation .pdf

Acknowledgments

I worked with my homework partner, Ava on this assignment. We texted throughout the week and met on Monday 5/7 and Wednesday 5/8 to discuss the assignment and make and practice our presentation.

Dr. Fitzpatrick also helped in class on 5/2 and in office hours on 5/8 with MATLAB and how to input our new variables and functions.

Except for what is noted above, this individual journal entry was completed by me and not copied from another source.

Angela C Abarquez (talk) 21:03, 7 May 2019 (PDT)