Moneil5 Week 2

From OpenWetWare
Jump to navigationJump to search

Helpful Links

Margaret J. ONeil

Assignment Pages:

Personal Journal Entries:

Shared Journal Entries:

Purpose

The scientific purpose of this assignment was to investigate how matlab can be used to plot vectors and calculate logistics curves based on given input variables.

WorkFlow & Methods

Part I: Create a script that includes the following elements

  • Define a vector u containing the elements 1,2,3,4,5,6,7,8,9,10 using the colon operation
    • In MatLab, I input the function u=1:10, and the output was u= [1.000, 2.000, 3.000, ..., 10.000]
  • Define another vector v containing elements that are the square of the vector x
    • To get v, I input the function v= u.^2 so that the squared function would apply to each part of the vector u. The output of this was v=[1.000, 4.000, 9.000, ... , 100.000]
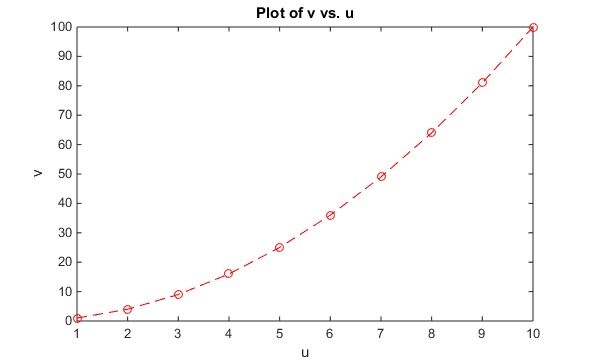
  • Plot v versus u (make sure you know what that sentence means!!) using circles on the points that are connected with dashed lines
    • The command plot(u,v,'ro--'); title('Plot of v vs. u'); xlabel('u'), ylabel('v') was used in order to obtain a plot of v vs. u using red circles as markers that were connected by a red dashed line.
  • Save your plot as a TIFF file
    • The plot was saved in the plot window as MO_1.25.17_BIO398-05S17_Week2_Modeling-Assignment_Part1.tif
  • Save your data into an excel spreadsheet using the MATLAB command xlswrite
    • The array [u;v] was saved into an excel spreadsheet by inputting the following commands:
      • filename'MO_1-25-17_BIOL398-05S17_Week2_Modeling-Assignment_Part1.xlsx'
      • A=[u;v]
        • Which output A= [1,2,3,4,5,6,7,8, 9, 10/1,4,9,16,25,36,49,64,81,100] with the slash indicating a new row in the matrix
      • xlswrite('MO_1-25-17_BIOL398-05S17_Week2_Modeling-Assignment_Part1.xlsx', A) which proceeded to generate an excel fie which contained the desired matrix made of vectors u and v

Part II: Create a script to compare logistic growth curves

  • Define a vector t starting at 0, ending at 1, in steps of 0.01.
    • To define t, the input was t=0:0.1:1
  • Define K = 10 and x0 = 2 for carrying capacity and initial population size.
    • k=10 and x0=2 were input as functions here

Plot logistic growth curves for growth rates 0.5,1.0,1.5, and 2.0.

    • The appropriate growth equation had to be determined here. I worked with Nika and Lauren and got help from Dr. Fitzpatrick in figuring out the correct notation, but eventually it was determined that the following general equation would provide the correct outputs:
      • y=(x0*k)./(k*exp(-r*t)-x0*exp(-r*t)+x0)
    • The following functions were then defined to get the appropriate r values:
      • r=0.5 => y1=(x0*k)./(k*exp(-0.5*t)-x0*exp(-0.5*t)+x0)
      • r=1.0 => y2=(x0*k)./(k*exp(-1.0*t)-x0*exp(-1.0*t)+x0)
      • r=1.5 => y3=(x0*k)./(k*exp(-1.5*t)-x0*exp(-1.5*t)+x0)
      • r=2.0 => y4=(x0*k)./(k*exp(-2.0*t)-x0*exp(-2.0*t)+x0)
    • In order to plot the equations, this step and the following step were combined, so the methods and workflow will continue on under the next bullet point
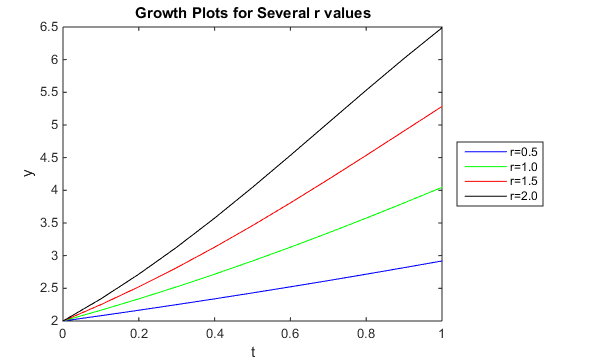
  • Plot these four curves together in one figure, and add appropriate labels, title, and legend.
    • In order for the curves to all be plotted in the same graph, the following command sequence was used:
      • plot(t,y1,'b')
      • hold on
      • plot(t,y2,'g')
      • plot(t,y3,'r')
      • plot(t,y4,'k')
      • title('Growth Plots for Several r values')
      • xlabel('t')
      • ylabel('y')
      • hold off
    • Once the plot with all 4 curves was generated, the label was created by going to the plot content feature and adding the legend. Once the legend was added, the legend names were changed so that the blue line, y1, was named "r=0.5", the green line, y2, was named "r=1.0," the red line, y3, was named "r=1,5", and finally the black line, y4, was named "r=2.0"
  • Save your plot as a TIFF file
    • From the plot window, save as was selected and the file was named MO_1.25.17_BIO398-05S17_Week2_Modeling-Assignment_Part2.tif

Results

The following were the results obtained from this week's modeling assignment; two plots, Figure 1 and Figure 2, as well as the excel spreadsheet of the matrix [u,v]

Data & Files

Part 1


Figure 1 This figure shows a plot of the defined vector v vs. the defined vector u. Please see Workflow & Methods, Part I to see how the plot was created

Media:MO_1-25-17_BIOL39805-S17_Week2_Modeling-Assignment_Part1.xlsx

Part 2

Figure 2. This figure shows logistics growth curves with the same function but a varying r value. Please see Workflow & Methods, Part II to see how the plot was created

Conclusion

The conclusion drawn from this week is that MatLab is a powerful computation tool that can be used for a variety of models, including simple plots (Part 1) as well as logistics growth models. In this exercise the purpose was achieved as MatLab was investigated more, and through trial and error the user was able to determine the correct commands to produce the desired models. The plot settings tools and file saving tools were also investigated, features which will likely prove to be beneficial in future assignments and projects.

Acknowledgments

This assignment could not have been completed without the assistance of Ben G. Fitzpatrick, who provided helpful advice via e-mail about the logistic growth curve. It also could not be completed without the aide and collaboration with Lauren M. Kelly and my homework partner, Nika Vafadari, as we worked together to double check eachothers input commands, and answered eachothers questions when needed.

Except for what is noted above, this individual journal entry was completed by me and not copied from another source. - Margaret J. Oneil 01:57, 26 January 2017 (EST)

References

Dahlquist, Kam D. (January 2017) BIOL398-05/S17:Week 2. Retrieved from http://www.openwetware.org/wiki/BIOL398-05/S17:Week_2 on January 25, 2017

Retrieved from "https://openwetware.org/mediawiki/index.php?title=Moneil5_Week_2&oldid=970356"