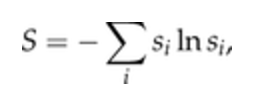Moneil5 Week 10

Helpful Links

Margaret J. ONeil

Assignment Pages:

• Week 1 Assignment
• Week 2 Assignment
• Week 3 Assignment
• Week 4 Assignment
• Week 5 Assignment
• Week 6 Assignment
• Week 7 Assignment
• Week 9 Assignment
• Week 10 Assignment
• Week 11 Assignment
• Week 12 Assignment
• Week 14/15 Assignment

Personal Journal Entries:

• Week 1
• Week 2
• Week 3
• Week 4
• Week 5
• Week 6
• Week 7
• Week 7 Re-visited
• Week 9
• Week 10
• Week 11
• Week 12
• Week 14/15

Shared Journal Entries:

• Week 1
• Week 2
• Week 3
• Week 4
• Week 5
• Week 6
• Week 7
• Week 9
• Week 10
• Week 11
• Week 12
• Week 14/15

Purpose

The purpose of this week's assignment is to learn more about the gene regulatory network modeling project through doing a journal club presentation on a given paper. This week for me I am focusing on presenting on and better understanding the role and structure of network motifs on the regulatory networks that are being modeled.

Pre-presentation work

Definitions

1. Motif

   A particular gene circuit organization that occurs in a gene network more frequently than would be expected by chance. The feed-forward loop is an example of a network motif that occurs prevalently in nature. (Network motif, 2016)

2. Gene regulatory network

   The graphical representation of the interactions among a series of genes to achieve a dynamic function. Genes are represented as nodes, and the interactions between genes are represented by edges. (Gene network, 2016)

3. Signal-transduction

   The process by which an extracellular signal (chemical, electrical, or mechanical) is converted into a cellular response. Typically, interaction of a hormone, growth factor, or other agonist with a specific membrane receptor leads to signal amplification by synthesis within the cell of one or more second messengers, or to activation of other downstream cascades, e.g. by phosphorylation of proteins. Chemical agonists that cross the cell membrane (e.g. steroid hormones) produce a cellular response without such amplification of the signal. Electrical signals flowing down axonal membranes lead to release of neurotransmitters at synapses. Their plasma membrane receptors are similar to those for hormones and growth factors, or are ion channels.

4. Nodes

   Any point in a network model or graph where lines or pathways intersect or branch, especially (in cognitive psychology) an element representing a concept in a semantic network of relations between nodes (relations such as x is a member of y or x is an attribute of y), each node being linked to certain other nodes in the network

5. Feedback loops

6. Suppression

   The cancellation, or reversal of the effects, of one mutation by another mutation, except where the second mutation causes a single base change at the same point as an earlier point mutation (in which case the term reversion is used). In intergenic suppression, the effects of a mutation in one gene are reversed by a mutation in another gene, usually because the second gene codes for a mutant tRNA (see frameshift suppressor). In intragenic suppression a mutation is cancelled by a second mutation close to the first in the same gene, normally within the same triplet, giving rise to a codon that is compatible with translation to a functional protein product. As an example, if the first mutation changed AGT (leading to the RNA codon for Ser) to ATT (giving a nonsense codon), a suppressor mutation might change the triplet to ATA (giving the RNA codon for Tyr); if the change Ser to Tyr led to a functional protein, suppression would be achieved.

7. Caenorhabditis elegans

8. Space state

References

Gene network - Oxford Reference. (2016, July 11). Retrieved March 29, 2017, from http://www.oxfordreference.com/view/10.1093/acref/9780199600571.001.0001/acref-9780199600571-e-7752?rskey=D4UIqf&result=3

Network motif - Oxford Reference. (2016, July 11). Retrieved March 29, 2017, from http://www.oxfordreference.com/view/10.1093/acref/9780199600571.001.0001/acref-9780199600571-e-7574?rskey=v54ywJ&result=9

Signal transduction http://www.oxfordreference.com/view/10.1093/acref/9780198529170.001.0001/acref-9780198529170-e-18234?rskey=e6185u&result=3

Node http://www.oxfordreference.com/view/10.1093/acref/9780199657681.001.0001/acref-9780199657681-e-5551?rskey=3kWMsE&result=18

Suppression http://www.oxfordreference.com/view/10.1093/acref/9780198529170.001.0001/acref-9780198529170-e-19001?rskey=tDrTlX&result=8

Outline

• What is the main result presented in this paper?
  • In this paper the authors use basin entropy and cycle length diversity to review 104 distinct three-node motifs and showed structural properties of a motif predict fundamental characteristics of that motif's space-state, which determines aspects of the motif's functional versatility.
  • The authors also found that the high-level properties they were investigating directly relate to "real" regulatory networks. This is because they found their two measures, basin entropy and cycle length diversity were shown to closely correspond to prevalence in the 13 connected motifs that were extensively studied in previous literature.
  • The relationship between structure and function that they found was deemed to likely be meaningful based on the close correspondence between the topological properties and enrichments of motifs found in regulatory networks.
• What is the importance or significance of this work?

  This work is showing that the structure of certain regulatory motifs can tell you about how a gene regulatory network behaves, and when used in a "real regulatory network" they found unfragmented and highly stable attraction basins of the networks served as a good template for implementation of a variety of gene expression patterns. Essentially what the authors found was that it was likely the topological functions they described in the space-state are influencing the biological evolution of regulatory networks. In Boolean networks, basin entropy and cycle length diversity are good measures for determining what is happening in the real world network.

• Create a flow chart to describe their methods. Answer the following questions if they are relevant to your article.

  The authors had three main buckets their methods fell into - characterizing the state space of network motifs, characterizing the structure of network motifs, and real-world regulatory networks.

  1. Characterizing the state space of network motifs

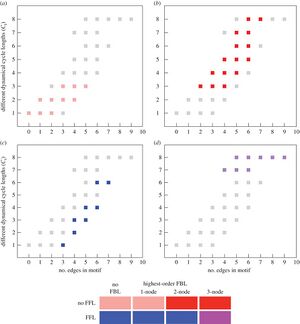
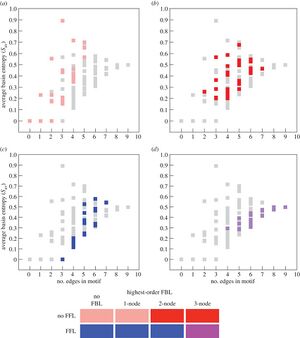
     • All possible network motifs for a 3-node motif produced 512 possible ways of connecting the nodes. Using dynamical transition graphs and feed-forward loop motifs, this was narrowed down to 5 dynamical graph topologies
     • Each dynamical graph topology was measured using basin entropy, and distinct cycle lengths

• What mathematical/statistical method did they use to analyze the data?

  Throughout the paper, the authors use graph statistics to analyze and measure network motifs and relationships found in the network. Of these statistics, they focus on 2 main measures, basin entropy and cycle length diversity.

  1. Basin entropy:

     

     s_i is the ith attraction basin as a fraction of the total space-state.

  2. Distinct cycle lengths

     C is the number of distinct cycle lengths where you reach a fixed point. For example, the graph in figure 1d has 1 cycle length of C=1 because you reach a fixed point when all three nodes have state 0.

• Briefly state the result shown in each of the figures and tables.
• Figure 1.

  

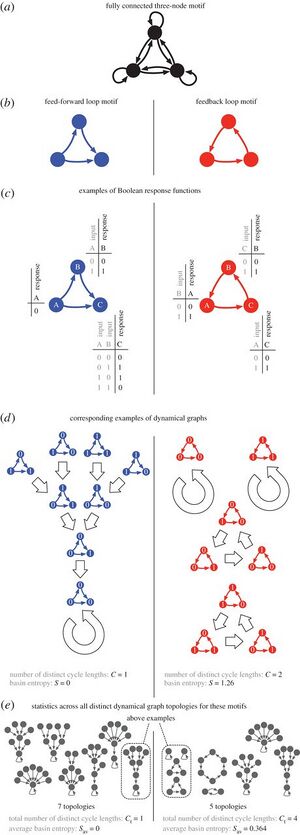
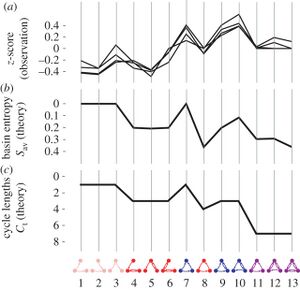
  Figure 1.

  This figure is depicting motifs as Boolean netoworks. In section, a, the network is a fully connected 3-node motif showing all possible connections. Part b shows two motifs as an example of feed forward and feedback loops, and part c shows how Boolean functions would be placed on those motifs. Part d shows the dynamical graphs of these examples, along with the distinct cell cycle lengths and basin entropies for each. Part e shows all the different topologies that can occur for the motifs, along with the total number of distinct cycle lengths and the average basin entorpy for each category. This figure serves as a breakdown of how the dynamical graph topologies will be used to intepret and analyze the network motifs.

• Figure 2.

  

  Figure 2.

• Figure 3.

  

  Figure 3.

• Figure 4.

  

  Figure 4.

• Figure 5.

  

  Figure 5.

Presentation

Media:MO.Week10.presentation.pptx

References

Ahnert, S. E., & Fink, T. M. A. (2016). Form and function in gene regulatory networks: the structure of network motifs determines fundamental properties of their dynamical state space. Journal of The Royal Society Interface, 13(120), 20160179. DOI: 10.1098/rsif.2016.0179

Dahlquist, Kam D. (2017) BIOL398-05/S17:Week 10. Retrieved from http://www.openwetware.org/wiki/BIOL398-05/S17:Week_10 on 28 March 2017.

Acknowledgments

• Except for what is noted above, this individual journal entry was completed by me and not copied from another source.

  Margaret J. Oneil 00:58, 30 March 2017 (EDT)