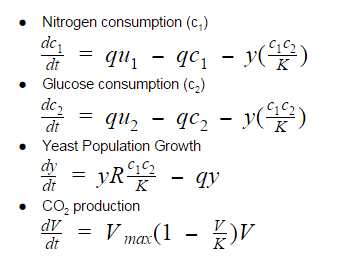Lkelly9 Week 6
From OpenWetWare
Jump to navigationJump to search
Navigation Links
- Lauren M. Kelly
- Assignment Page
- Individual Journal Entry
- Shared Journal Page
Purpose
- The purpose of this assignment is to hypothesize what the impact of ammonium feet rate is on a quantity of interest in a chosen journal article and devise a system of differential equations that captures the important behaviors using state variables that are necessary to the process.
Workflow/Methods
- First, i picked one of the "Gaining a Better Understanding of the Fermentation/Respiration Switch" project and read the Albertin et al (2011) paper. Attached is a PDF of the notes that I took on this paper as I was reading it. I used these notes to better understand how different variables were related and write a system of differential equations.
- Based on the reading, I concluded that the relationship between nitrogen consumption, K (population limit), CO2 production (Vmax) was important in regards to the fermentation respiration switch.
- Using the Week 5 Assignment to push me in the right direction, I delineated state variables and devised a system of differential equations that could represent the relationship between nutrient consumption (nitrogen and glucose), the yeast population growth, and the production of CO2.
Results
Hypothesis
- Based on the findings in the Albertin et al (2011) paper and our work in previous assignments, it can be inferred that the nitrogen consumption is positively correlated to K (maximum population) and Vmax (maximal CO2 production rate). Increasing K will increase the amount of nitrogen the yeast can consume and the amount of CO2 the yeast can produce. A multiplicative nutrient use model will be utilized to display this relationship.
- It is assumed that the yeast are being grown in a chemostat.
State Variables
- y = concentration of yeast
- c = concentration of nutrient (nitrogen or glucose)
Parameters
- q = dilution rate
- u = concentration of nutrient fed into the reactor (nitrogen or glucose)
- Nt = population of yeast at time t
- K = carrying capacity
- V = CO2 concentration
- Vmax = maximum CO2 production
Differential Equations
- Assuming the yeast is being grown in a chemostat:
Explanation
- Nitrogen Consumption
- qu1 represents the nitrogen being fed into the reactor
- qc1 represents the nitrogen being taken out of the reactor
- y[(c1c2/K)] represents the amount of nutrient being assimilated by the yeast
- Glucose Consumption
- qu2 represents the glucose being fed into the reactor
- qc2 represents the glucose being taken out of the reactor
- y[(c1c2)/K] represents the amount of nutrient being consumed by the yeast
- Yeast Population Growth
- yR[(c1c2)/K] represents the growth rate of the yeast in the reactor as they consume the nutrients.
- qy represents the yeast being taken out of the reactor at a constant rate
- CO2 Productions
- Vmax = the maximum CO2 production
- V = the concentration of CO2
- The CO2 concentration is limited by the carrying capacity (K)
Conclusion
- The Albertin et al (2011) article showed me that a wide variety of factors play a role in aerobic and anaerobic respiration in yeast. One relationship in particular that stood out to me was the positive correlation between K and nitrogen consumption and between K and Vmax. K, according to the paper, is the main component of CO2 production variation. As the maximum population size (carrying capacity) increases, more CO2 can be produced by that population. The differential equations that I wrote will ideally display the relationship between the nutrient consumption (nitrogen and glucose), K (or population size) and the production of CO2. It is not certain at this moment whether or not my hypothesis is correct/these equations accurately represent the yeast population, but with further investigation I hope to improve my understanding.
Acknowledgements
- Worked with Cameron M. Rehmani Seraji in Seaver 120 on February 22nd.
- Referenced the Week 5 Assignment in order to figure out a set of equations.
- Except for what is noted above, this individual journal entry was completed by me and not copied from another source.
Lauren M. Kelly 21:56, 22 February 2017 (EST)
References
- Dahlquist, Kam D. (2017) BIOL398-05/S17:Week 6. Retrieved from http://www.openwetware.org/wiki/BIOL398-05/S17:Week_6 on 22 February 2017.
- Albertin, W., Marullo, P., Aigle, M., Dillmann, C., de Vienne, D., Bely, M., & Sicard, D. (2011). Population Size Drives Industrial Saccharomyces cerevisiae Alcoholic Fermentation and Is under Genetic Control . Applied and Environmental Microbiology, 77(8), 2772–2784. http://doi.org/10.1128/AEM.02547-10