Lkelly9 Week 2

Navigation Links

• Lauren M. Kelly
• Assignment Page
  • Week 1
  • Week 2
  • Week 3
  • Week 4
  • Week 5
  • Week 6
  • Week 7
  • Week 9
  • Week 10
  • Week 11
  • Week 12
  • Week 14/15

• Individual Journal Entry
  • Week 2
  • Week 3
  • Week 4
  • Week 5
  • Week 6
  • Week 7
  • Week 7 Redo
  • Week 9
  • Week 10
  • Week 11
  • Week 12
  • Week 14/15

• Shared Journal Page
  • Week 1
  • Week 2
  • Week 3
  • Week 4
  • Week 5
  • Week 6
  • Week 7
  • Week 9
  • Week 10
  • Week 11
  • Week 12
  • Week 14/15

Electronic Lab Notebook

Purpose

The scientific purpose of my investigations was to plot two vectors, u and v, on a graph and to model the logistical growth for four different rates on one plot.

Workflow/Methods

Part I: Create a script that includes the following elements

• • Define a vector u containing the elements 1,2,3,4,5,6,7,8,9,10 using the colon operation
    • u = [1:10]
  • Define another vector v containing elements that are the square of the vector
    • v = u.^2
  • Plot v versus u (make sure you know what that sentence means!!) using circles on the points that are connected with dashed lines
    • plot(u,v)
    • Add title: title('V vs. U')
    • X-axis label: xlabel('u')
    • Y-axis label: ylabel('v')
  • Save your plot as a TIFF file
  • Save your data into an excel spreadsheet using the MATLAB command xlswrite
    • Declare the file name: filename='insertfilenamehere'
    • Put u and v together in a vector: A=[u;v]
    • Save into an excel sheet: xlswrite('insertfilenamehere',A)

Part II: Create a script to compare logistic growth curves

• • Define a vector t starting at 0, ending at 1, in steps of 0.01.
    • t = [0:0.01:1]
  • Define K = 10 and x0 = 2 for carrying capacity and initial population size.
  • Plot logistic growth curves for growth rates 0.5,1.0,1.5, and 2.0.
    • For r=0.5: y1=(x0*K)./(K*exp(-0.5*t)-x0*exp(-0.5*t)+x0)
    • For r=1.0: y2=(x0*K)./(K*exp(-1.0*t)-x0*exp(-1.0*t)+x0)
    • For r=1.5: y3=(x0*K)./(K*exp(-1.5*t)-x0*exp(-1.5*t)+x0)
    • For r=2.0: y4=(x0*K)./(K*exp(-2.0*t)-x0*exp(-2.0*t)+x0)
  • Plot these four curves together in one figure, and add appropriate labels, title, and legend.
    • plot(t,y1,'m',t,y2,'r',t,y3,'b',t,y4,'k')
  • Save your plot as a TIFF file

Results

Data and Files

• 
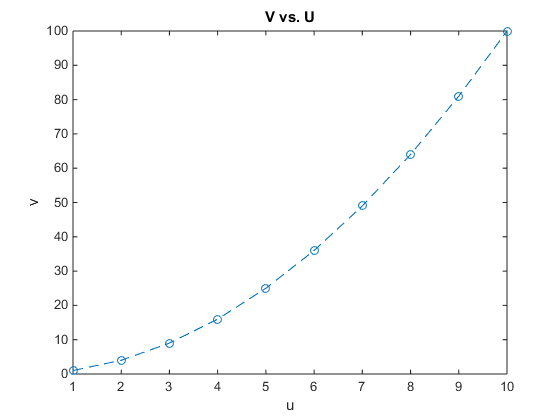
• Figure 1. This plot displays the relationship between vectors u and v. Please refer to the workflow above to see how this plot was created.
• Vector u and v Data
• 
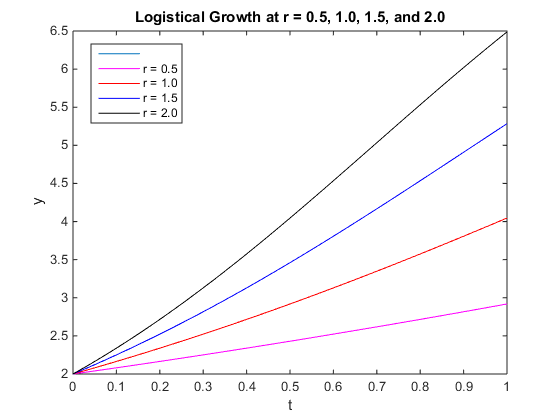
• Figure 2. This plot displays the logistic growth curves for r = 0.5, 1.0, 1.5, and 2.0. Please refer to the workflow above to see how this plot was created.

Conclusion

My main finding for today's project was that MATLAB can be manipulated in a variety of ways to model data. Furthermore, the logistic growth curves, assuming I executed them correctly, were fairly linear and they did not level off at any point. I accomplished my purpose of plotting vectors u and v and plotting four different logistic growth curves in the same figure.

Acknowledgements

• I worked with my homework partner Cameron M. Rehmani Seraji face-to-face in the computer lab outside of class. We worked on the MATLAB portion of the assignment together.

• I worked with Margaret J. ONeil and Nika Vafadari face-to-face in the computer lab outside of class. We worked on the logistic growth curve together.

• I worked with Ben G. Fitzpatrick through email one time. He helped me with the logistic growth curve.

• Except for what is noted above, this individual journal entry was completed by me and not copied from another source
• Lauren M. Kelly 01:22, 26 January 2017 (EST)

References

Dahlquist, Kam D. (2017) BIOL398-05/S17:Week 2. Retrieved from http://www.openwetware.org/wiki/BIOL398-05/S17:Week_2 on 25 January 2017.