Lkelly9 Week 5

Navigation Links

• Lauren M. Kelly
• Assignment Page
  • Week 1
  • Week 2
  • Week 3
  • Week 4
  • Week 5
  • Week 6
  • Week 7
  • Week 9
  • Week 10
  • Week 11
  • Week 12
  • Week 14/15

• Individual Journal Entry
  • Week 2
  • Week 3
  • Week 4
  • Week 5
  • Week 6
  • Week 7
  • Week 7 Redo
  • Week 9
  • Week 10
  • Week 11
  • Week 12
  • Week 14/15

• Shared Journal Page
  • Week 1
  • Week 2
  • Week 3
  • Week 4
  • Week 5
  • Week 6
  • Week 7
  • Week 9
  • Week 10
  • Week 11
  • Week 12
  • Week 14/15

Purpose

• The purpose of this assignment is to assess various models for multiple nutrients in the chemostat and demonstrate the algebra behind finding the equilibrium equations for Model 2. Model 2 will also be used to model the relationship between ammonia concentration, glucose concentration, and yeast biomass, similar to the journal club paper.

Workflow/Methods

• Part 1
  • Assessed Model One, the additive model, and concluded why it might not be the best choice
• Part 2
  • Put dy/dt in terms of q, and plugged in this value for q in the dc1/dt and dc2/dt equations in order to show that Model Two's non-trivial equilibrium is characterized by the presented equations.
• Part 3
  • Please view the attached algebra below for the exact methods of finding the y*, c1*, and c2* values.
  • Excel was utilized in order to recreate the journal club paper Figure 1(a) with my findings.
• Part 4
  • Worked out the algebra for Model Three using the same methods as Part 2 in order to find the analogous equations.

Results

1. Explain why Model One, the additive model, may not be the best choice.
   • This model may not be the best choice because, in terms of the journal club paper, the yeast require both glucose and ammonia in order to grow. If the ammonia were to run out, for example, the yeast would not be able to only live on glucose until that ran out as well.
2. Work out the algebra to show that Model Two’s “non trivial” equilibrium is characterized by the equations below, for yeast, residual ammonium, and residual glucose, respectively.
   • Algebra for Model Two's "non-trivial" equilibrium
3. Set q=0.15, V1=110, V2=180, K1=2.5, K2=10, R=15, u2=100. With these values, and the values of u1 in the journal club paper for ammonium feed concentrations, find the equilibrium values of yeast, residual ammonium, and residual glucose. Recreate the journal club paper Figure 1(a) plot with your findings.
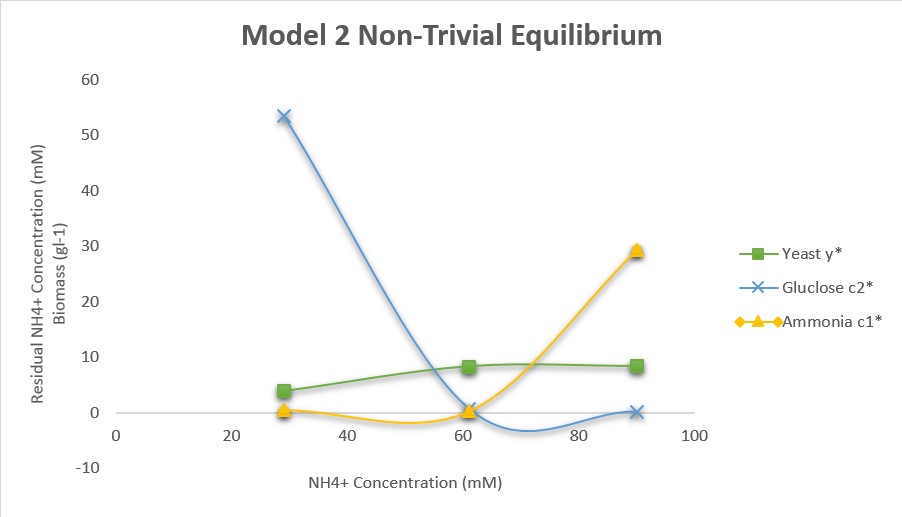
   • Figure 1. Recreation of Figure 1(a) from the journal club paper.
   • Algebra for Question 3. Page 1/3
   • Algebra for Question 3. Page 2/3
   • Algebra for Question 3. Page 3/3
4. Are there analogous equations to the ones of Part (2) for Model Three? If so, what are they?
   • Model 3 is almost identical to Model 2, with the exception of the yeast growth rate being limited to the minimum of the individual conversion rate functions. It appears that the algebra, however, would be almost the same as in Model 2. The algebra for these equations is attached below.'
   • Algebra for analogous equations

Conclusion

• The multiplicative nutrient use model is best used when the organism has access to two different nutrients that it can use to grow. It models the consumption of both nutrients at once, which is important in determining when a certain nutrient is limiting. The equilibrium values of these models represent when the yeast are using as much nutrients as they can and are maintaining a stable population.
• The re-creation of Figure 1(a) from the journal club paper behaved in a similar way to the original figure. As the ammonia concentration exceeds 61 mM, the biomass and the residual ammonia concentration increase. The biomass and the glucose level both appear to reach equilibrium as the concentration of ammonia exceeds 61 mM and becomes excess. When the ammonia concentration is at 29 mM, the primary source of nutrients is the glucose, which is shown by the fast decrease in glucose concentration. In the journal club paper, however, the glucose level was fixed at 100 mM and did not decrease because it was being constantly fed into the chemostat. This is one point that this re-creation does not model as well.

Acknowledgements

• Worked on the algebra for the Model Two equilibrium with Margaret J. O'Neil on Sunday, February 12th in Seaver 120.
• Worked on the equilibrium values for Question 3 with Cameron M. Rehmani Seraji and Margaret J. O'Neil on Wednesday, February 15th in Seaver 120 and in the Tri Beta Study Session.
• Except for what is noted above, this individual journal entry was completed by me and not copied from another source.

Lauren M. Kelly 22:27, 15 February 2017 (EST)

References

• Dahlquist, Kam D. (2017) BIOL398-05/S17:Week 5. Retrieved from http://www.openwetware.org/wiki/BIOL398-05/S17:Week_5 on 12 February 2017.
• ter Schure, E. G., Sillje, H. H., Verkleij, A. J., Boonstra, J., & Verrips, C. T. (1995). The concentration of ammonia regulates nitrogen metabolism in Saccharomyces cerevisiae. Journal of bacteriology, 177(22), 6672-6675.