Brianna N. Samuels-Week 12

From OpenWetWare
Jump to navigationJump to search

Purpose

  • to develop a chemostat model for yeast using the Tai et al paper and MATLAB

Methods

Developing a Yeast-in-the-Chemostat Model

Reconsider Table 1 of the Tai et al (2007) journal club paper and do some research on chemostats.

  • Find some reference material (books, papers, preferably not random internet sites) on chemostat growth processes, so that you can answer these questions.
    • The yield quantity Y Glu/X: this is a ratio of what quantities? Be specific and relate to the 2-nutrient chemostat model from class.
    • The flux qGlu is a ratio of what quantities? Be specific and relate to the 2-nutrient chemostat model from class.
    • Convert residual glucose and residual ammonia from mM to grams.
    • Determine the length of time the chemostat is operated before data is collected.
    • Determine as many model parameters as you can from these data: use the "warm" data and both glucose- and ammonium-limited data.

Develop a simulation model for a 2-nutrient chemostat.

  • Modify the MATLAB files chemostat_script.m and chemostat_dynamics.m to simulate a 2-nutrient chemostat. You will find those codes in the zipfile here. This task will require the equations we developed in class.
    • Use what parameters you have determined from the data to simulate the system.
    • Do the graphs show the system going to steady state?
    • Do the steady states match the Table 1?
    • Be sure to save the graphs and upload them to your journal.

Results

  • Y Glu/x : shows the dry weights in units of grams of yeast to grams of glucose.
  • qGLU : shows the concentration of glucose over the product of time and dry weight of the yeast.
  • time= 100 hours prior to data collection

Conversions

  • Glucose @ 12° = 0.5g (residual glucose)
  • Glucose @ 12° = 1.18g (residual ammonium)
  • Glucose @ 30° = 0.05g (residual glucose)
  • Glucose @ 30° = 1.11g (residual ammonium)
  • Ammonium @ 12° = 16.2g (residual glucose)
  • Ammonium @ 12° = .027g (residual ammonium)
  • Ammonium @ 30° = 15.33g (residual glucose)
  • Ammonium @ 30° = 0.0036g (residual ammonium)

Parameters

Warm Glucose

  • Xo = 1
  • Yo = 0.05
  • Zo = 1.18
  • r = 0.07
  • K = 0.002
  • L = 0.0444
  • u = 25
  • v = 5
  • E = 14.3
  • F = 0.259
  • q = 0.03
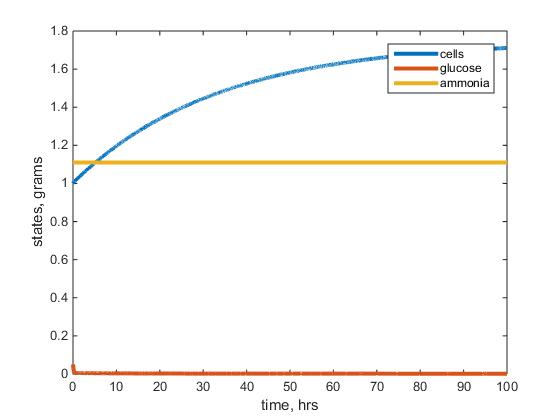
  • Figure 1: This figure depicts the warm glucose model results after running the model with given parameters listed above. The blue line represents the biomass, red the residual glucose and yellow the residual ammonium left in the chemostat.

Figure 1

Warm Ammonium

  • r = 1.7
  • K = 23
  • L = 0.325
  • u = 46
  • v = 0.65
  • ep = 25
  • F = 0.372
  • q = 0.03
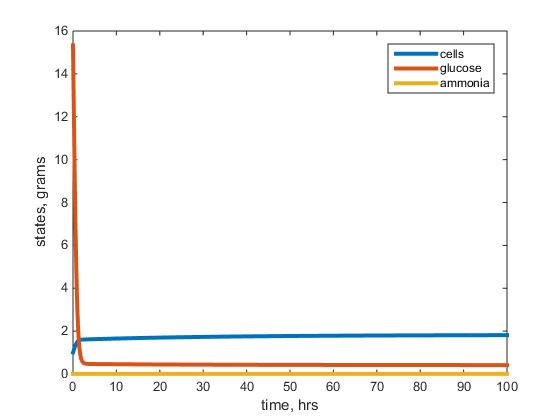
  • Figure 2: This figure depicts the results of the the warm ammonium limited model after running the model with given parameters listed above. The blue line represents the biomass, red the residual glucose and yellow the residual ammonium left in the chemostat.

Figure 2

  • I would say overall the cell mass went to steady state as well as my other parameters but it literally started and ended in a steady state for my ammonium and glucose curves.
  • The steady states do not match that in the table (not exactly sure what I was doing wrong but I know something definitely was wrong on my end).

Scientific Conclusion

I was able to run the model. I kept getting a horizontal line every time I ran it which didn't make any sense. I even tried using the same parameters as my partner and I still kept getting horizontal lines when he didn't. I believe there might have been an issue with my coding even though it looked the same as others. I would overall say it was somewhat successful in the sense that I was able to run the model, but not successful in the sense that I do not believe I did anything right.

Acknowledgments

  • Homework Partner: Austin Dias: Met face to face and texted about the assignment frequently.
  • Saw how to cite the Tai et al. Papers from Leanne
  • Except for what is noted above, this individual journal entry was completed by me and not copied from another source.

References

Retrieved from "https://openwetware.org/mediawiki/index.php?title=Brianna_N._Samuels-Week_12&oldid=1066312"