Brianna N. Samuels-Week 14

From OpenWetWare
Jump to navigationJump to search

Purpose

  • to find r using Arrhenius' equation for 12, 15, 20, 25, and 30 degrees
  • investigate whether E should be a function of y

Methods

  1. Use the Arrhenius equation (rate = A*exp(-B/(R*T)) to model the temperature dependence of the chemostat reaction.
    • Figure out the constants A and B from the rate data in the TaiParamsRevised.m file.
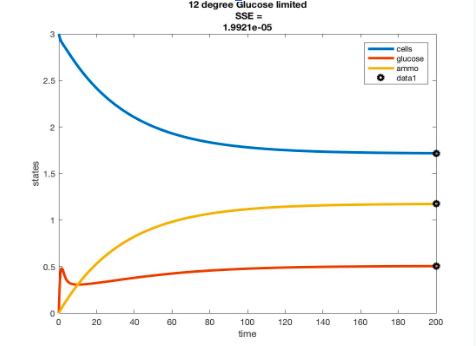
    • Simulate the chemostat for T = 15,20, 25 degrees C conditions and graph the time courses of the biomass and nutrients.
  2. Investigate the glucose efficiency/waste constant (that is not really a constant?) for the glucose-limited and ammonium-limited conditions.
    • Note the values of E for glucose-limited and ammonium-limited conditions.
    • For each temperature (12, 30), find a function E(y) that matches the two points of (y,E) data.
    • Modify the chemostat_2nutrient_dynamics.m file to use the functions you've created.
    • Compare the resulting simulation to the previous one.

Your individual journal should detail your efforts, and your 15-minute presentation should cover these topics:

  1. A brief intro to the chemostat problem of Tai et al (2007).
  2. The data we've extracted from the paper and other sources.
  3. Your temperature investigation.
  4. Your efficiency/waste investigation.
  5. Discussion and reflection on your findings.

Results

Solving for r

  • r=Ae^(-B/RT)
    • A = 4.9 * 10^11
    • B = 68258.79
    • T = 12,15, 20, 25, 30 (convert to Kelvin)
    • R = 8.134
  • will be using Glucose limited data
  • other parameters came from Tai et al. 2007

Glucose 15 degrees Glucose 20 degrees Glucose 25 degrees

Investigating E

  • determine E is a function of y
  • should be modeled as a straight line on MATLAB
  • replace in MATLAB wherever we see E with E(y) equation

E equations Glucose 12 limited Glucose 30 limited Ammonium 12 limited Ammmonium 30 limited File:Biomathematical Modeling Final.pdf

Acknowledgments

  • Homework Partner: Ali texted consistently, met face to face a couple times to work on presentation, as well as attended office hours together
  • Attended office hours for Dr. Fitzpatrick
  • Except for what is noted above, this individual journal entry was completed by me and not copied from another source.

References

Retrieved from "https://openwetware.org/mediawiki/index.php?title=Brianna_N._Samuels-Week_14&oldid=1067137"