Macie Duran Week 2

From OpenWetWare
Jump to navigationJump to search

Template

Link to Template

User Page

Macie M. Duran

Assignments

Journals

Class Journals

Purpose

The purpose of this week's assignment is to demonstrate the importance of modeling a pandemic or epidemic. Using models, we can better understand the safety precautions that must be taken when an outbreak occurs.

Methods & Results

  1. I watched the video The role of applied math in real-time pandemic response: How basic disease models work. After finishing the video, I recorded two questions I had:
    • How can this be applied to coronavirus when we know that recovered people can become susceptible again in a fairly short period of time? Would we add in a new group of people who have recovered, and may have some antibodies, but are still considered susceptible?
    • How do we figure out rates 1 and 2 for SARS-CoV-2 or other novel viruses? How much time would it take to estimate those rates? Can we base the rates on other similar viruses, such as SARS-CoV?
  2. I read the information on this website, and interpreted the graphs using the following information:
    • When I=0, there are no infected individuals in the population. Therefore, the disease will not spread.
    • The red line (representing the number of daily infected individuals) increases rapidly, meaning the disease is spreading quickly. It maxes out around day 26, and then begins to fall, indicating that most susceptible people have been infected and will soon join the recovered group.
    • The green line (representing the number of recovered people) also rises quickly, but not as quickly as the red line. This indicates that the recovery rate is fast, but the infection rate is faster.
    • The green line nearly reaches 1000, but not quite. It tops off at 980, meaning 20 people did not recover. These people are accounted for by the purple line, which represents the cumulative mortalities. Because only 20 out of 1000 cases resulted in death, we can assume the disease is not very deadly.
  3. I explored an interactive SIR model, Epidemix.
    • I clicked the "Start" button in the middle of the page to begin.
    • I decided to work with a Deterministic Homogeneous COMP model. I chose this model because it is more precise, in that it is mathematically based. There are no random variations, so any changes made to the parameters will produce the same result every time you run the model.
    • I observed the initial model, and then manipulated the parameters and observed the effects it had on the model.

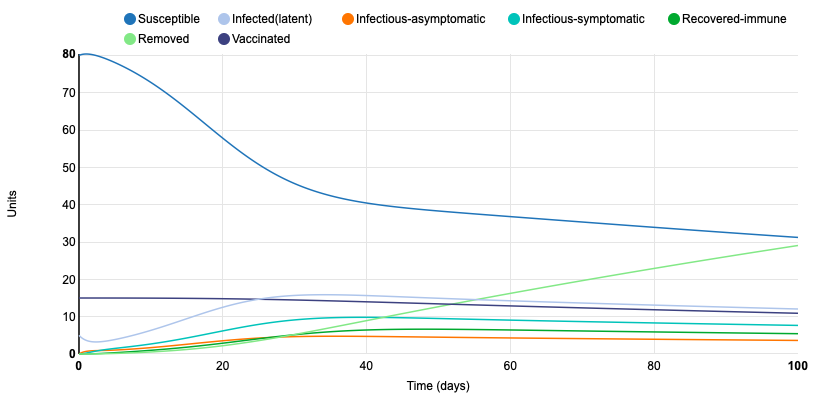
Initial SIR Model

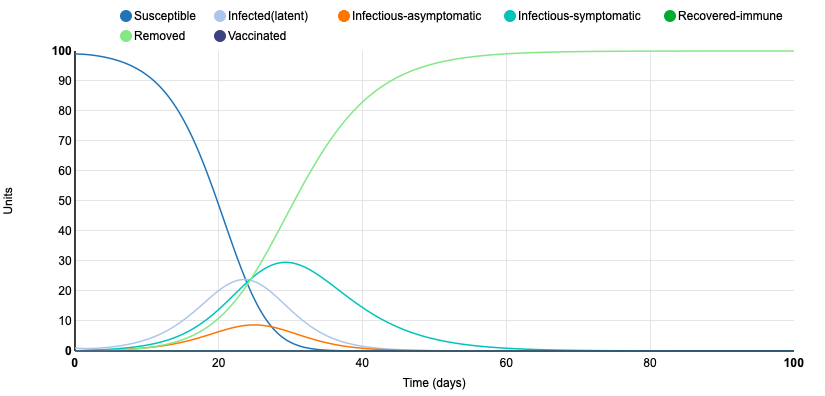
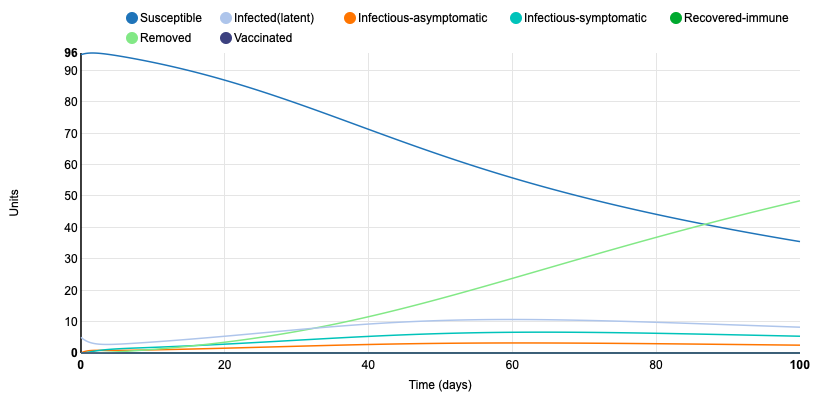
This is the initial graph for the Deterministic Homogeneous COMP model. There is a closed population of 100 people. The graph breaks up the population into five groups: Susceptible, Infected (latent), Infectious-asymptomatic, Infectious-symptomatic, and Removed. Because the population is closed, all 100 units are removed, rather than being replaced, at the end of the infectious period. Initially, 99 units are susceptible and 1 is infectious (latent). The daily number of effected contacts per unit is 0.62, and the disease transmission is frequency-dependent. The latent period lasts 4 days, the asymptomatic infectious period is 1.5 days, and the infectious symptomatic period is 6.5 days. Because of this, by day 12, the number of susceptible units begins to quickly decrease, while the number of removed units quickly increases. There are smaller peaks for the number of latent, asymptomatic, and symptomatic units, as individuals move through the three stages and into the removed group. On day 64, all 100 units are removed.

Parameter Changes on SIR Model

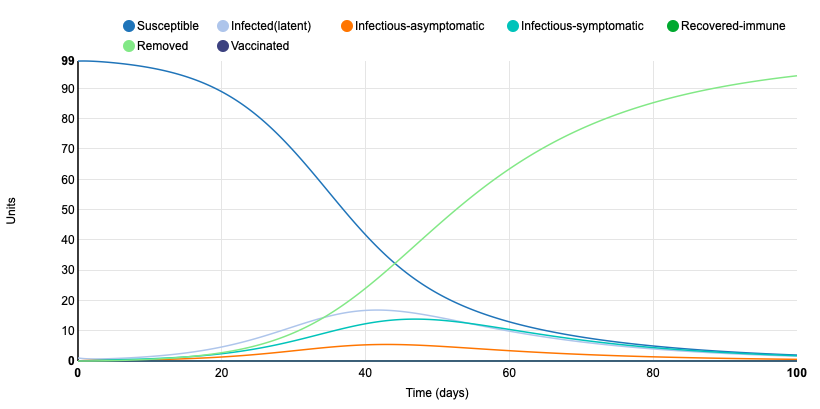
First, I changed the population from closed to open, with a unit being present in the population for a duration of 10 days. This drastically changed the duration of the disease in the population. In the closed population, all units were removed by day 64. In the open population, by day 100, 2 units are still susceptible, 2 units latent, 1 is infectious-asymptomatic, and 2 are infectious-symptomatic. This demonstrates how a disease can run its course in a much shorter period of time when members of the population are not traveling. An open population allows for more susceptible and infected people to come into contact with one another, prolonging the epidemic. This shows why travel restrictions are important in controlling the spread of a disease.

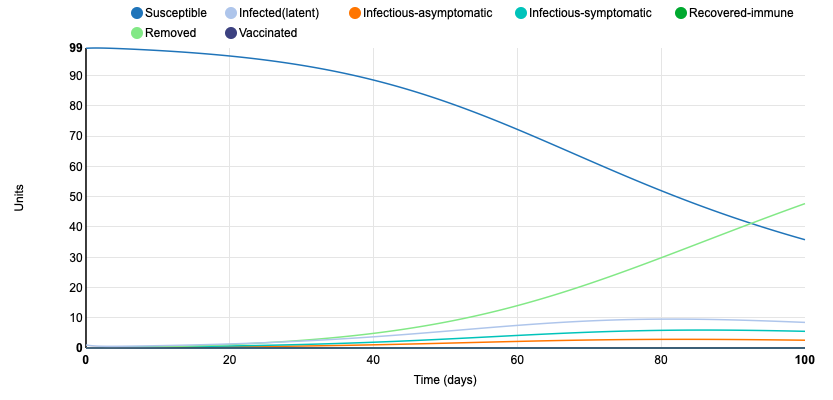
Next, I changed the duration of a unit in the population from 10 days to only 6 days. This extended the duration of the disease even more. After 100 days, only 47 units are removed and 36 are still susceptible.

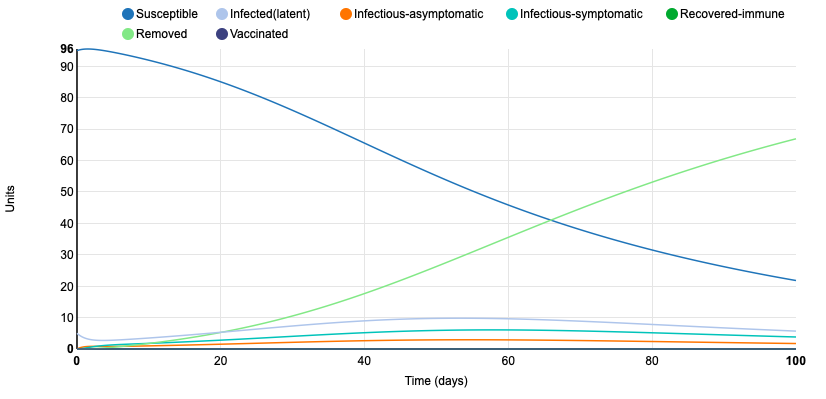
The third parameter I changed was the number of infected units at the start of the simulation. Instead of having only one infected individual, I changed it to five infected units. This alters the chances of a susceptible unit coming into contact with an infected unit. Because of this, the slope representing susceptible units decreased more quickly and the number of removed individuals increased more quickly. This shows that the disease would run its course at a faster rate.

Then, I changed the parameters so that only some units were removed at the end of the infectious period, and some became susceptible again. I set the probability of being removed after infection to 0.65. This once again caused the disease to be prolonged. Because some units are exiting the infectious stage and returning to the group of susceptible units, it will take a longer period of time for the disease to run its course. I felt that this was relevant to COVID-19, since we see recovered people becoming susceptible again after a few months. Rather than gaining immunity, there is a chance that they could run through the full infectious period once again, and also spread the disease to more people around them.

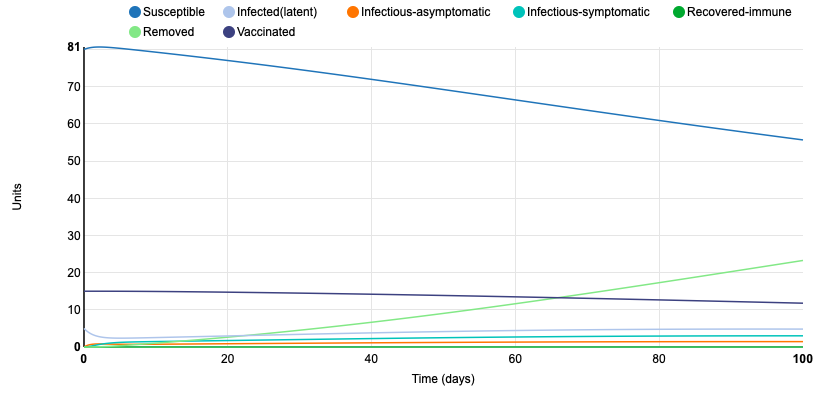
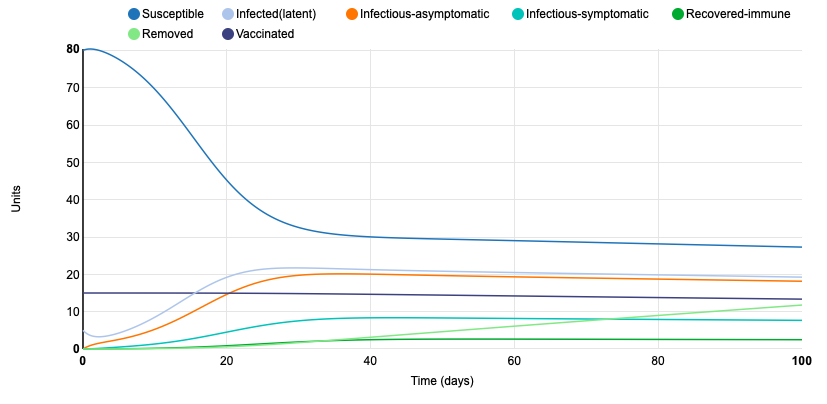
Next, I added in a control strategy -- vaccination. I set the proportion of vaccinated units to 0.15. This slowed the rate of infection by quite a bit. At day 100, 56 units were still susceptible and only 23 were removed. Throughout the simulation period, the amount of units accounted for in the infected (latent), infectious-asymptomatic, and infectious-symptomatic groups never totaled more than 10. Because a portion of the population was vaccinated, the probability of spreading the disease decreased.

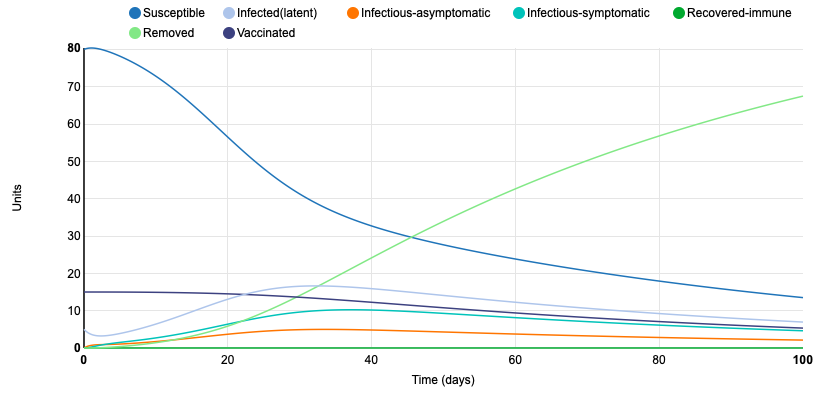
Because the last graph showed a very slow rate of infection, I decided to change the daily number of effective contacts per unit from 0.62 to 1. This once again sped up the infection rate. At the end of the 100 day period, only 14 units were still susceptible and 67 were removed. Altering this parameter displays the importance of social distancing. A greater amount of contact correlates with a higher rate of transmission from infectious individuals to susceptible individuals.

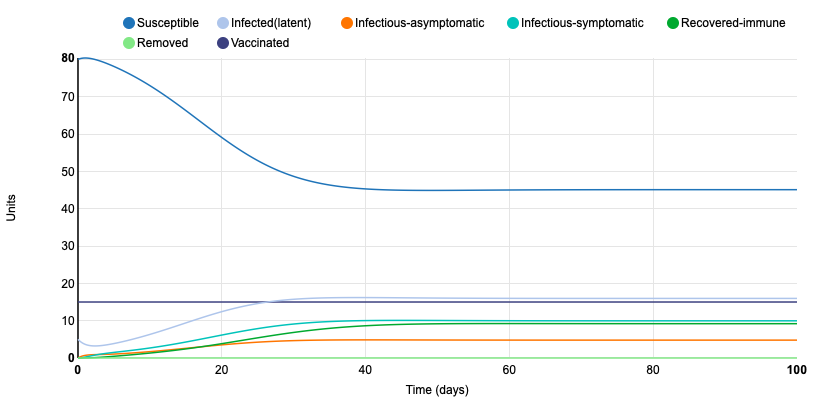
I added another infectious state into the model -- recovered units. I altered the parameters so that each infected unit recovers, and remains immune until they are removed. This caused all of the lines to level out by day 30. This change demonstrates how immunity slows the rate of infection.

Next, I altered the recovery parameters. Rather than setting all the units to recover after infection, I set it so only some recovered. I set the probability of being removed after infection to 0.25. This caused the line representing the amount of removed units to increase, and the number of susceptible units to continue decreasing, rather than leveling out early on in the simulation.

My ninth parameter change extended the infectious period. I changed the length of the asymptomatic infectious period from 1.5 days to 10 days, and the length of the symptomatic infectious period from 6.5 days to 14 days. This would cause the rate of infection to increase, since the units are spreading the disease for a longer period of time. In a real world example, a long asymptomatic period would be especially dangerous because individuals may not be aware that they are sick. In the case of COVID-19, infected people can be completely asymptomatic and unknowingly spread the virus when coming into contact with others. Once again, this shows why social distancing is important, not only for those that are aware they are sick, but for everyone.

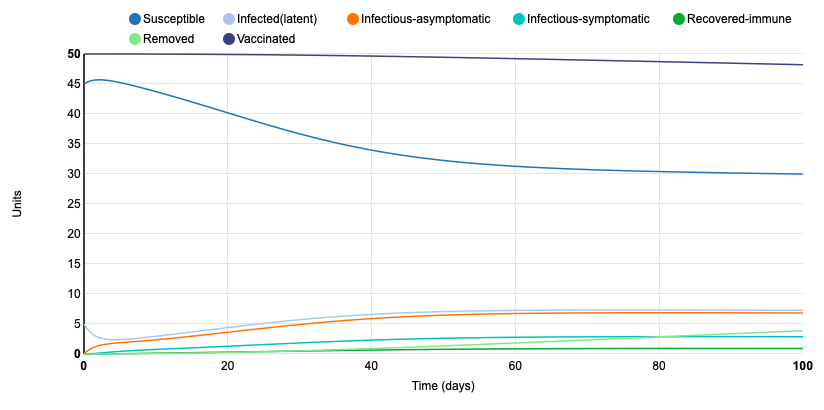
The last parameter I changed was the proportion of vaccinated units from 0.15 to 0.5. This drastically changed the model because the number of susceptible units never exceeded 46. When the proportion of vaccinated units was 0.15, the model began with 80 susceptible units. This just goes to show how important vaccination is in a population. Having a large portion of vaccinated individuals slows the transmission of the infection and helps to protect members of the population that are not vaccinated. The amount of infected units remains level by about day 40. At that point, no more than 18 individuals are infected at a time.

Giordano Article

  1. I looked at Figure 1 of the Giordano et al. (2020) article.
    • The authors creating this model accounted for several features of the COVID-19 pandemic. Compared to a basic model that groups individuals into Susceptible, Infected, and Recovered, this model has several different infectious states. For example, they account for a diagnosis step. Not everyone that is infected is immediately diagnosed, due to the possibility of being asymptomatic. Some heal without ever being diagnosed, and some become symptomatic and then receive a diagnosis. There is also a stage called Threatened, meaning the infected individual reaches a critical condition. Once someone is in the threatened state, they can either move to the healed state or the extinct state.
    • One public health implication in this model is the importance of getting regularly tested. Because it is fairly common to be asymptomatic, it is crucial that individuals are being careful not to come into contact with too many people around them, and that testing is readily available to everyone.

Comic

  1. I looked at https://xkcd.com/2355/ this comic.
    • This comic is funny because it's poking fun at the people who create these models, implying that only a stereotypical nerd would enter this type of profession.

Conclusion

Understanding how to create and interpret SIR models are useful tools to have when predicting and analyzing an epidemic or pandemic. These models allow us to determine precautionary measures, such as social distancing, to help slow the rate of transmission and "flatten the curve."

Acknowledgements

  1. I contacted my homework partner, Yaniv Maddahi, once regarding changing the parameters for the Epidemix portion of the assignment.
  2. I copied and modified the protocol shown on the Week 2 page.
  3. I used the Epidemix website to generate SIR model graphs.
  4. Except for what is noted above, this individual journal entry was completed by me and not copied from another source.

(Macie Duran (talk) 21:01, 16 September 2020 (PDT))

References

Epidemix. (2020). Retrieved 16 September 2020, from https://www.epidemix.app/#

Epstein, J., 2008. Why Model?. [online] Jasss.soc.surrey.ac.uk. Retrieved September 16, 2020, from http://jasss.soc.surrey.ac.uk/11/4/12.html.bak

Giordano, G., Blanchini, F., Bruno, R., Colaneri, P., Di Filippo, A., Di Matteo, A., & Colaneri, M. (2020). Modelling the COVID-19 epidemic and implementation of population-wide interventions in Italy. Nature Medicine, 26(6), 855-860. doi: 10.1038/s41591-020-0883-7

OpenWetWare. (2020). BIOL368/F20:Week 2. Retrieved 15 September 2020, from https://openwetware.org/wiki/BIOL368/F20:Week_2

SIR Model. (2020). Retrieved 16 September 2020, from http://www.pandemsim.com/beta/SIRmodel.html

University COVID Model. (2020). Retrieved 16 September 2020, from https://xkcd.com/2355/

Youtube. 2020. The Role Of Applied Math In Real-Time Pandemic Response: How Basic Disease Models Work [Video]. Retrieved 10 September 2020, from https://www.youtube.com/watch?v=Ewuo_2pzNNw&feature=youtu.be&ab_channel=NIMBioS

Retrieved from "https://openwetware.org/mediawiki/index.php?title=Macie_Duran_Week_2&oldid=1089250"