Nika Vafadari Week 4

From OpenWetWare
Jump to navigationJump to search

Electronic Lab Notebook Week 4

Purpose

To create a chemostat model of the growth of yeast and nutrient concentrations using Matlab and analyze the changes in concentrations when the parameter variables and initial conditions are altered.

Work Flow and Methods

Question 1

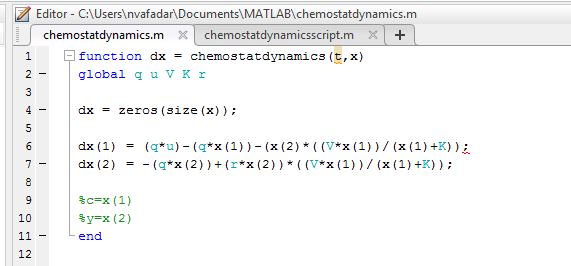
  • First created the functions on Matlab using the two equations from the Week 4 Exercise handout
    • titled the function chemostatdynamics

Chemostat Dynamics Function

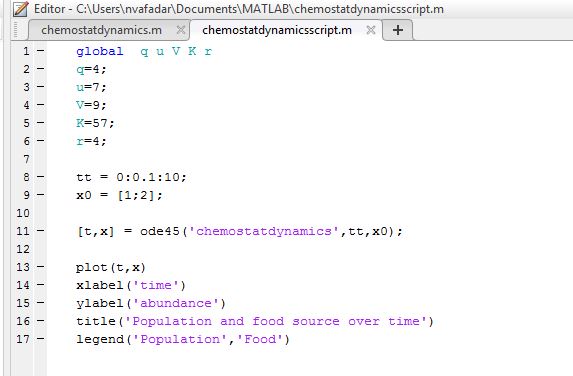
  • Next created a corresponding script in order to graph the function

Chemostat Dynamics Script

  • After changed values of the variables (q, u, r, V, K) as well as the initial conditions in order to see how the plot of the population changed and find the values of c and y that allow the system to be equilibrium

Question 2

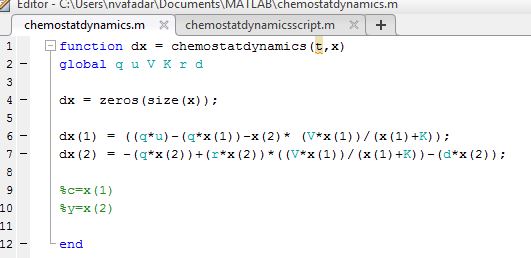
  • First I edited the function to add a term/variable (death rate) for linear mortality

Linear Mortality Function

  • Next the corresponding script was edited to include the new variable/parameter (d) by adding it to the global variables then setting d equal to a number.
  • The function was then plotted, changing the values of the variables once again, specifically looking at the effect of changes in the value of d on the plot.
  • Once again values were found for c and y that allow the system to be equilibrium

Question 3

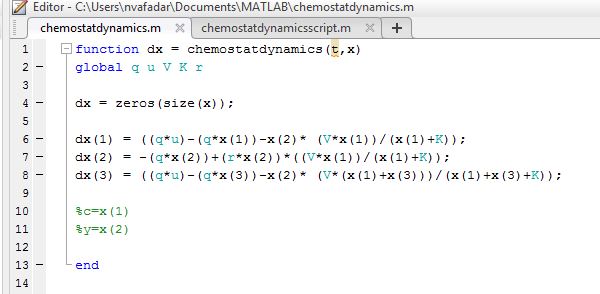
  • First the previous function for linear mortality was edited, removing the mortality term and instead adding a third equation to account for the second nutrient

Two Nutrients Function

  • The script was then adjusted to add a third initial condition, by expanding from x0=[1;3]; to x0=[1;3;2];
  • The function containing the two nutrients was then plotted

Results

  • Question 1
    • a)
    • state variables:
      • y=concentration of yeast cells
      • c=concentration of nutrients
    • parameters: q, u, r, K, V
    • b) Find values of c and y that hold the system in equilibrium
      • y=0 and c=u
    • c) Simulate this system with different values for the constants and the initial concentrations of nutrients and cells. Make any observations about how the system behaves.
      • Found below are two examples of the plots created during the simulations

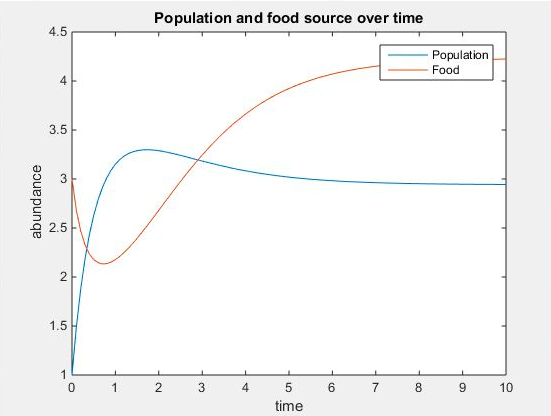
Chemostat Plot 1

  • Figure 1. The figure above displays the concentration of yeast cells and nutrients over time at q=2, u=4, V=9, K=50, r=4 at the initial starting conditions of x0=[1;3] with t at intervals of 0.1 from 0 to 10.

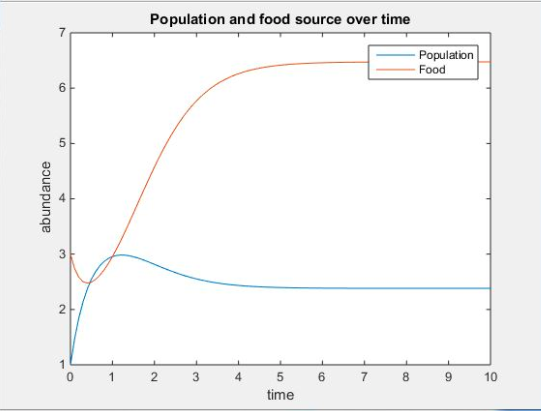
Chemostat Plot 2

  • Figure 2. The figure above displays the concentration of yeast cells and nutrients over time at q=2, u=4, V=11, K=50, r=4 at the initial starting conditions of x0=[1;3] with t at intervals of 0.1 from 0 to 10.
  • Observations:
    • The two figures above display that the lower the value of V, the closer the concentrations of the nutrients and yeast are to each other.
    • Both display that a change in concentration of both the nutrients and yeast from initial conditions takes place followed by a leveling off of the concentrations.
    • As the concentration of nutrients decreases, the concentration of the yeast increases. Eventually both concentrations level off.
  • Question 2: What changes if we return a mortality term to the population equation? Repeat b and c for a linear mortality term.
      • Found below are two examples of the plots created during the simulations for linear mortality

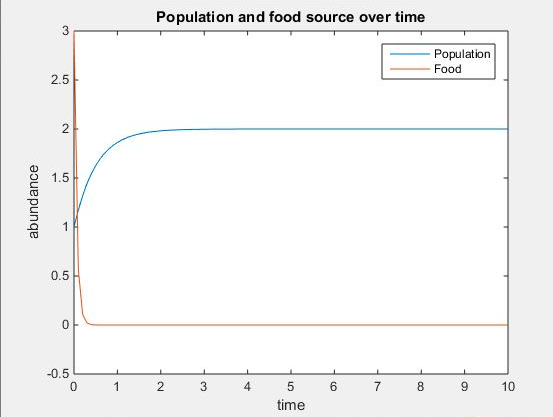
Chemostat Plot 3

  • Figure 3. The figure above displays the concentration of yeast cells and nutrients over time at q=2, u=2, V=2, K=30, r=4, d=15 at the initial starting conditions of x0=[1;3] with t at intervals of 0.1 from 0 to 10.

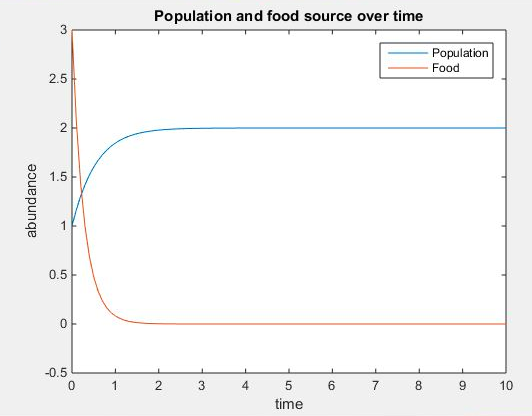
Chemostat Plot 4

  • Figure 4. The figure above displays the concentration of yeast cells and nutrients over time at q=2, u=2, V=2, K=30, r=4, d=2 at the initial starting conditions of x0=[1;3] with t at intervals of 0.1 from 0 to 10.
  • Observations:
    • The two figures display what occurs when all variables are kept constant including the initial conditions and time, while the value of d is altered. The comparison of the two plots shows that d affects the rate of change of the concentration of both food and yeast.
    • Yet equilibrium was found to exist at the same values of y=0 and c=u


  • Question 3: Create a model with two nutrients, both of which are required for the population to grow.

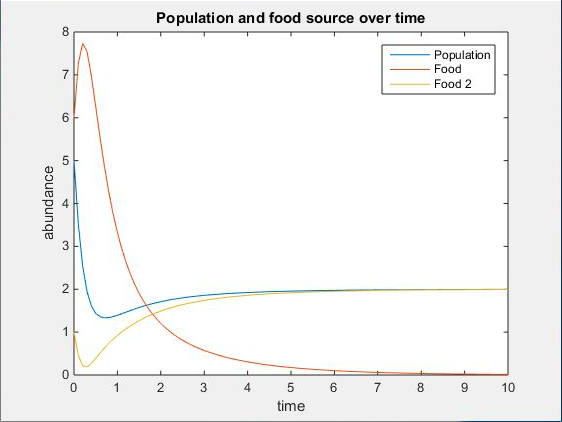
Two Nutrient Plot

  • Figure 5. The figure above displays the two nutrient plot for the values of q=3, u=2, V=10, K=30, r=4 at the initial starting conditions of x0=[5;6;1] with t at intervals of 0.1 from 0 to 10.
  • Observations:
    • As the concentrations of the two nutrients decrease then level off, the population of yeast decreases then levels off as well.
    • In addition there was a decrease in the population of the yeast observed with the introduction of the mortality term as seen by the reduced concentration levels of the yeast compared to the concentration levels in the plots from Question 1 even though the starting conditions were the same.

Data Files

Matlab Chemostat Script

Conclusion

Through the course of this modeling exercise I was able to explore manipulate the parameter variables, initial conditions, and time of a chemostat model in order to observe the effects of the various parts of the model, such as a specific parameter variable, on the concentrations of the yeast and nutrients. The three conditions explored, including a typical chemostat model with one nutrient, one with two nutrients and one with a linear mortality term, allowed me to observe the key features of a chemostat model. For example, it was found that while the yeast and nutrient levels both leveled off, neither plummeted to zero, supporting the key feature of a chemostat, which is that there is a constant fixed flow of nutrients and yeast in and out.

Acknowledgments

Nika Vafadari 21:06, 8 February 2017 (EST):

References

Dahlquist, Kam D. (2017) BIOL398-05/S17:Week 4. Retrieved from http://www.openwetware.org/wiki/BIOL398-05/S17:Week_4 on 8 February 2017.

Useful Links

Retrieved from "https://openwetware.org/mediawiki/index.php?title=Nika_Vafadari_Week_4&oldid=972810"