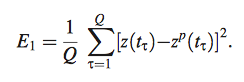Nika Vafadari Week 10
Electronic Lab Notebook Week 10
Purpose
To analyze the journal article by Vu and Vohradsky, which discusses the use of a non linear model in identifying the regulators of target genes associated with the cell cycle in yeast and correctly determining their function as an activator or repressor.
Preparation for jornal Club 2
Journal Club Presentation Slides
Biological/ Mathematical Terms
- Putative: something that is generally accepted or assumed Source
- Proteomic: the entire complement of proteins of an organism or cell Source
- Nonlinear differential equation: unlike linear equation power of equation is not one Source
- Specificity of prediction: the proportion of negatives that are observed that were in fact predicted to be negatives Source
- Levenberg-Marquardt method: standard method used for solving non linear least squares problems through minimization of the sum of the square of errors Source
- Parallelized: to make a program/ adapt it to run on a processing system that is parallel thus similar to it Source
- Gene Regulatory Network: A grouping or set of genes that are found to work together in controlling a particular function in a cell Source
- Algorithm: the set of formulas (usually in a set or specific order) or complete procedure used for solving a problem Source
- Co-ordinatley Compared Genes: Refers to the eukaryotic genes which have their own promoter and control elements. These genes do not need to be next to each other but have the same control elements Source
- Histogram: graphical representation that focuses on relaying the shape or underlying distribution of a continuous set of data Source
Outline
Main Result Presented in Paper
- Goal: use the approximation/ estimation of the expression profile of target gene to pick set of potential regulators for that specific target gene
- identify true regulators by determining which ones best model the profile of the target gene
- check for correct identification of regulators by comparing results to YEASTRACT database
- used a non linear model as opposed to a linear one
- Found that non linear model correctly identifies the regulators of target genes associated with the cell cycle in yeast/ determines their functions as activator or repressor
- compared to linear model, non linear model give better results in terms of correct identification of the regulator and better fit to gene expression profile of target
(further discussed in discussion section below)
Significance of Work
Introduction
Regulation of gene expression
- DNA (gene) —> RNA molecules and functional proteins
- For regulation to occur—> transcriptional regulatory proteins must recognize promotor sequence in order to bind RNA polymerase and start transcription reaction to environmental stress & cell development can lead to modification/change in gene expression
DNA microarrays
- visualize and record change in gene expression over the time (duration of cell cycle/developmental processes) by looking at the change in mRNA levels
- to understand relationship between regulators/ target genes and the network interactions that result
- these networks are what lead to changes in the amount of RNA/ changes in gene expression
Cell cycle control
- well studied in Saccharomyces cerevisiae leading to the establishment of large transcriptomic databases that include the changes in RNA synthesis throughout the cell cycle
- Goal: collect microarray gene expression data (genome wide) pertaining to cell cycle in yeast—> analyze through clustering methods —> identify cell cycle controlled genes
- based on assumption that the expression profile of a specific target gene is the result of action of upstream regulator (transcriptional regulator)
Methods
Previous methods
- grouped genes based on which promoter the transcriptional regulators bind to instead of similarity in pattern of gene expression
- identified potential networks through the use of differential equations in order to develop a generalized linear model to predict the pattern of transcription of a specific gene
- Wolf and Wang: used fuzzy logic
- Nachman et al.: used dynamic Bayesian networks with a kinematic model
- Bar-Joseph: used gene expression analysis and genomic info alongside one another
- Wang et al. and Makita et al.: extending the work of Bar-Joseph, incorporated promoter sequence analysis into gene expression analysis
Alternative method presented in paper
- replaces linear model with model using nonlinear differential equation
- Procedure applied
- starts by selecting set of potential regulators —> 184 chosen
- select set of specific target genes within S. cerevisiae —> 40 genes selected
- select genes from within the set of potential regulators to apply model to in order to see if it fits the gene expression profile of the specified gene correctly
- repeat for selected target genes and potential regulators
- determine true regulators by identifying regulators that model the profile of the target gene correctly
- Procedure applied
Results
Dynamic model of transcriptional control
- Model Assumptions
- the relationship/ interaction between regulators and target genes is repeated over time
- combinatorial control by regulators exists/causes change in gene expression of a target gene
Equation 1
- represents target gene expression level z at time t + dt
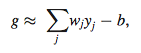
- g= regulatory effect for specific gene
- yj= expression levels of regulators at time t
- wj= regulatory weights of genes controlling target gene
- j= 1, 2,…,m ( m= number of regulators controlling gene)
- b= parameter that represents delay of transcription initiation/ unspecified bias from regulatory effects of gene expression
Equation 2
- rate of expression of a target gene (dz/dt)
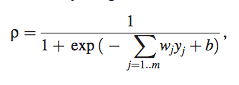
- p= regulatory effect g of regulators j transformed by sigmoidal transfer function (regulatory effects of other genes)
- x= effect of degradation (x=k.z.)
Equation 3
- models control of target gene expression z
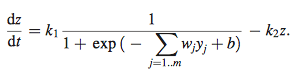
- k2= rate constant of degradation of product of target gene
- k1= maximal rate of expression
Equation 4
- simplified version of equation 3 that only considers one transcriptional factor
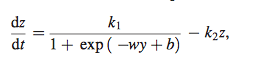
- y= approximated with a polynomial of degree n (shown below in equation 5)
Equation 5
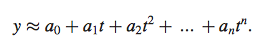
- used least squares minimization procedure to calculate coefficients {a0, . . , an} from experimental gene expression profile
- assumed same weight of error for all measured points
- degree n= must be chosen individually for each experiment based on number of data points in profile and fluctuation due to experimentation to reflect rate of changes in gene expression within the specific experiment (for yeast cell cycle chose n=6)
Equation 6
- to identify the gene profiles that minimize the mean/average square error function
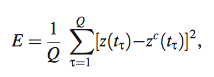
- Z= z(t) = expression profiles of target gene at time points t for Q data points (1,2,…,Q)
- Y= y(t)= expression profiles of regulator gene at time points t for Q data points
- Q= number of data points (data points calculated by equation 4 model)
- z^c(t)= reconstructed profiles of Z at time points t for Q data points
Equation 7
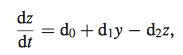
- In order to minimize error function (equation 6), data was entered into both nonlinear model and linear model to compare the calculated parameters (w, b, k1, k2) represented by d
Computational algorithm
- Goal: use the approximation/ estimation of expression profile of target gene to pick set of potential regulators for a specific target gene
- potential regulators for specific target gene were chosen from pool of 184 transcriptional regulators using equation 4/ least square minimization and minimizing error function (equation 6)
- estimated regulator gene profiles using polynomial of degree n to avoid both missing data points and fluctuating gene expression profiles due to experimentation
- solved equation 4 numerically using ode45 function in MATLAB (Runge–Kutta procedure) and optimized parameters with least squares minimization loop (using standard Levenberg– Marquardt procedure)
- repeated 100 times for each regulator-target combo with random values for parameters at start of optimization
- results compared to linear model using equation 7 in place of equation 4
Overall algorithm:
- use equation 5 to fit regulator genes with polynomial of degree n
- choose specific target gene
- choose possible regulator from large pool of potential ones
- use least squares minimization (equation 4) on target gene/ regulators & error function (equation 6)
- repeat starting at step 3 for all potential regulators
- choose best fit regulators that match criteria
- repeat for all the target genes starting at step 2
Dataset selection
- used eukaryotic cell cycle dataset (Spellman et al.) to evaluate model which includes..
- gene expression changes at 18 time points over 2 cell cycle periods
- 6178 open reading frames on microarray chip
- identified 800 genes associated with cell cycle according to their expression
- however, number of regulators controlling cell cycle < 800, therefore pool of 184 chosen by researchers for this experiment based on YEASTRACT database and previous papers
- chose same 40 target genes from Chen et al. paper to compare data
Inference of regulators
- data put into log base 2 of ratio (actual value of the mRNA over standard value that was the same for every time point)
- prior to use of algorithm —> data squared/ least squares minimization applied to target genes for potential regulator
Equation 8
- estimates unknown real gene expression profile of target gene
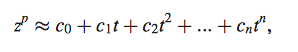
- approximation takes into account error due experiment/ natural fluctuations by polynomial fit rather than statistical model, which could have been used
Equation 9
- most likely potential regulator determined by identifying the regulator profile that best models the target profile (eq. 4) and minimizes error (eq. 6)
- therefore, chose regulators with an error (E) from eq. 6 less than or equal to the deviation (E1) computed using eq. 9
- the small the value of E the better the regulator fits the target gene profile
- best regulators= those that have a recognizably smaller E than other regulators therefore fitting the target profile better
Table 1
- complete list of 40 target genes with summary of correct identification, indicating which regulators for specific target genes were actually confirmed to be regulators for that gene in the YEASTRACT database (contains current, but incomplete knowledge)
- m= total number of regulators identified based on criteria
- min (m)= which number regulator the first correctly identified one was in the list of regulators for that target gene (listed from smallest to largest E value)
- min (m) lin= based on linear model instead of non linear
- E= defined by equation 6 (non linear model eq. 4 & linear model eq. 7)
Key results drawn from Table 1
- out of the best regulators —> 35% correctly identified
- false positive (FP) rate -which is the amount of predicted regulators not in database (ratio of false positive identified regulators over total amount of potential regulators) = low of 1.1%
- when E < E1 used as criterion —> 37.5% correctly identified but rate of FP double
- two other methods E < 1.1 * E1 & E < 1.2 * E1 —> found to increase correct identification percentage, but also increase FP rate
- 4 target genes found to cause most of the increases in FP rate: YOR323C, YJL155C, YDR285W, YAL018C
- due to fact that almost any of the regulators could model their profiles
- in addition, these 4 profiles displayed high fluctuations, therefore having large E1 values (deviation from experimental data)
- due to difficulty in evaluation data of 4 genes excluded
- specificity of prediction (Sp = (N - FP)/N) —> indicates number of experiments necessary to verify results of algorithm
- N= total number of potential regulators
- looking at min (m) —> most correctly identified regulators identified within first 5 regulators in list
- for 90% of target genes (36/40) correctly identified regulator identified within first 10 regulators in list
- all target genes had at least one correctly identified regulator identified within first 21 in list
- Compared sign of weight of regulators (+ = activator, - = repressor) to YEASTRACT database
- 77.8% of regulators correctly identified as activators or repressors
- Sources of inaccuracies/ error in prediction of function (activator vs repressor) vs actual function
- YEASTRACT database incomplete
- high error due to experimental noise
- least squares minimization (used to calculate target gene expression profile) could have not reached optimal solution, meaning the actual regulator could have not been identified
- attempted to reduce this issue by testing different initial parameter values through several runs of least squares minimization for set that gave best solutions (repeated 100 times for best estimation of profile of specific target gene)
Figure 1
- displays expression profiles of target gene, best fitting regulator, reconstructed target gene for 12 genes that are regulated by the cell cycle
- A group: repressors
- B group: activators
- x-axis: 18 time points
- y:axis: expression relative to time point zero
- graph name lists target gene then regulator
- repressors- opposite trend as target genes
- activators- same trend as target gene
Comparison with linear model
- compared results of non linear model to linear one (eq. 7) as shown in Table 1
- regulators listed from smallest to largest value of E (eq. 6)
- min (m)= which number regulator the first correctly identified one was in the list of regulators
- Figure 2 = histogram of distribution of these values
- A (left) non linear model
- B (right) linear model
- non linear model seems to have better fit (one degree better) & better results
- when error of measurement in microarray experiment set at 10%, meaning E value of regulator should be within 10% of E=0.0268
- 9 genes excluded for non linear model & 37 excluded for linear model
Discussion
- used an algorithm based on a non linear model that models all possible regulator-target gene combos and determines which regulators best fit the gene expression profile of that specified gene correctly
- true regulators determined by comparing results to YEASTRACT database
- found that non linear model correctly identifies the regulators of target genes associated with the cell cycle in yeast and correctly determines their function (activator or repressor)
- compared to linear model, non linear model give better results in terms of correct identification of the regulator and better fit to gene expression profile of target.
- linear model gave lowest fit and lowest prediction ability when compared to both non linear model and model presented in Chen et. al (generalized linear model)
- when 3 models were compared (non linear, linear, Chen et. al) found that all 3 gave different results for the sets of genes
- shows how models are often created to focus on specific case or aspect
- for example, Chen et. al found to have improved fit since it included more regulators at each step, however this occurred at the cost of accuracy when it came to predicting non-documented regulators for a target
- the non linear model overall showed good accuracy and reasonable fit
- identified correct regulators and their functions
- since the model captures the behavior of transcriptional regulation/ provides info on influence of possible regulators and correctly predicts regulators, it can act as a useful tool in interpreting gene expression time series
- however, large scale network may require a large number of computations that may be unrealistic
- requiring improvements in speed and incorporation of additional independent genome-wide location data, DNA sequence data, etc.
- Other drawbacks/ limitations still exist
- since possible regulators are chosen from larger pool of ones defined independently for example through sequence analysis for similarity, regulators may remain unidentified
- genes that aren't involved in regulation may have expression profiles that satisfy the minimization criterion therefore FPs from this would have to be sorted out independently
- the involvement of a regulator could me masked by inhibition of its activity due to another regulator that may not be in the set of potential regulators leading to false negative
- proteins that mediate transcriptional regulation arise from post-translational modification, therefore use of proteomic data may be more appropriate instead of the microarray data
Acknowledgments
- Various sites referenced linked and referenced next to each term were used to define the biological terms.
- The equations, figures and key info pertaining to the construction of the model and execution of the experiment, such as definition of variables, were copied and pasted from the article referenced below.
- Except for what is noted above, this individual journal entry was completed by me and not copied from another source.
- Nika Vafadari 05:24, 27 March 2017 (EDT):
References
- Dahlquist, Kam D. (2017) BIOL398-05/S17:Week 10. Retrieved from http://www.openwetware.org/wiki/BIOL398-05/S17:Week_10 on 27 March 2017.
- Vu, T. T., & Vohradsky, J. (2007). Nonlinear differential equation model for quantification of transcriptional regulation applied to microarray data of Saccharomyces cerevisiae. Nucleic acids research, 35(1), 279-287. doi: 10.1093/nar/gkl1001
Useful Links
- Nika Vafadari
- Course Home Page
- Weekly Journal Entries
- Shared Journal Pages
- Assignment Pages
- Template:Nika Vafadari