Flow and Pattern Asymmetries
Asymmetries in Microfluidics
Asymmetric patterns are often leveraged in microfluidic mixing as attributed by the fluid's laminar behavior. Characterized by low Reynolds numbers in microchannels, mixing cannot be achieved by simple back and forth mixing due to reversible flow. To address the challenge of mixing with laminar flow, novel methods involving asymmetries and asymmetric patterns have been explored for a variety of applications. [1]
Both passive and active mixing methods utilize asymmetric patterns to enhance mixing. Notable passive mixing methods that use asymmetries consist of the Herringbone mixer, twists and bends, and recirculating plugs and droplets. Active mixing methods such as acoustic micro-mixing and pneumatic mixers incorporate asymmetries as well. To best understand the applications of asymmetric patterns in microfluidics, it is important to be aware of the fundamentals of mixing.
Fundamentals of Mixing
Mixing can be described as a physical process through which two or more components are combined in a way such that a uniform distribution is achieved. It is a fundamental unit operation that is needed for a variety of applications. Due to differences in macroscale and microscale flow phenomenon, mixing occurs differently, and hence, the design and implementation of mixers also differs greatly between these two systems. To understand the forces that govern the respective systems and contribute to mixing, there are several key dimensionless numbers and mathematical relationships to be considered.
Diffusion and Advection

The mixing of components primarily occurs through two different phenomena: diffusion and advection. Diffusion is the process through which individual molecules move via random (Brownian) motion. This can be described by Fick's first law,
[math]\displaystyle{ J = - D \nabla c }[/math],
where [math]\displaystyle{ J }[/math] is the flux, [math]\displaystyle{ D }[/math] is the diffusivity of the respective species, and [math]\displaystyle{ \nabla c }[/math] is the concentration gradient, which serves as the driving force of the process. If two species with different concentrations are contained in an isolated environment, molecules from each species will diffuse into the other until the overall concentration becomes uniform; it is at this point where the species are effectively mixed. The time required for mixing to occur, the mixing time ([math]\displaystyle{ t_{mix} }[/math]), is dependent on the diffusivity ([math]\displaystyle{ D }[/math]) of the species and the length over which diffusion must occur, which is known as the striation length ([math]\displaystyle{ l_{st} }[/math]). [2] The mixing time can be expressed by the equation,
[math]\displaystyle{ t_{mix} }[/math] ~ [math]\displaystyle{ \frac {{l_{st}}^2}{D} }[/math].
Based on this relationship, it is evident that decreasing the striation length is necessary for decreasing the mixing time, which can be seen in Figure 1. [2] This idea leads into the fundamental concepts of mixing: decreasing the distance over which diffusion must occur and the process of diffusion itself.
In contrast to diffusion, advection is the process through which molecules move via the movement of the bulk, otherwise known as flow. Compared to diffusion, advective mixing is much faster and much more efficient. The degree of diffusive and advective mixing that takes place is dependent on the type of fluid flow, which can be characterized by the Reynolds number.
Reynolds Number (Re)
The Reynolds number (Re) is defined as the ratio between inertial and viscous forces, and it is used to define the flow regime of a fluid. Reynolds number is found using the following equation,
- [math]\displaystyle{ \mathrm{Re} = \frac{\rho v L}{\mu} }[/math],
where [math]\displaystyle{ \rho }[/math] is the density of the fluid, [math]\displaystyle{ v }[/math] is the velocity of the fluid, [math]\displaystyle{ L }[/math] is the characteristic length of the fluid, and [math]\displaystyle{ \mu }[/math] is the dynamic viscosity of the fluid.
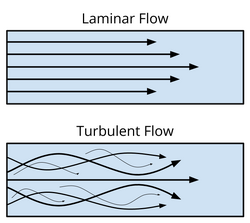
At low Reynolds number (Re < 2300), viscous forces dominate over inertial forces; these viscous forces dampen any disturbances in the flow, and as a result, the fluid moves in a smooth, layered fashion through the channel. [3] This type of flow is known as laminar flow. At high Reynolds number (Re > 4000), inertial forces dominate over viscous forces; in this case, the fluid has enough kinetic energy to overcome the damping viscous forces, meaning that any disturbances in the flow propogate, resulting in turbulent flow. [3] The differences between these two flow regimes are shown in Figure 2.
At the macroscale, fluids can take on a variety of flow regimes. By altering the characteristic length of a channel or increasing the linear velocity, the Reynolds number can be increased, and the flow can be made turbulent. This turbulence or irregularity in the flow is one of the driving forces for advective mixing.
At the microscale, the characteristic length is particularly small, resulting in Reynolds number between 0.01 and 100, restricting the flow to the laminar flow regime. [3] The parallel streamlines of the fluid means that no advective mixing can occur, and instead, only diffusion can occur between the parallel streams. Therefore, microfluidic systems are solely dependent on diffusive mixing. This is further illustrated by the Péclet number.
Péclet number (Pe)
The Péclet number (Pe) is a dimensionless number that describes the ratio between advective and diffusive forces, and it is also used to describe the ratio between advective and diffusive timescales. The Péclet number is defined as
[math]\displaystyle{ Pe = \frac{(Advection \, rate)}{(Diffusion \, rate)} = \frac {t_{diff}}{t_{adv}} = \frac {L^2/D}{L/U} = \frac {UL}{D} }[/math],
where [math]\displaystyle{ U }[/math] represents the linear velocity, [math]\displaystyle{ L }[/math] represents the length scale of the flow, [math]\displaystyle{ D }[/math] represents the mass diffusion coefficient, [math]\displaystyle{ t_{diff} }[/math] represents the characteristic time for diffusion, and [math]\displaystyle{ t_{adv} }[/math] represents the characteristic time for advection. [2]
In the case of microfluidic devices, where mixing relies solely on diffusion, the time for mixing to occur can be defined as:
[math]\displaystyle{ t_{mix} = t_{diff} = t_{conv} Pe }[/math].
Therefore, the length required for mixing to occur can be defined as:
[math]\displaystyle{ L_{mix} = U t_{mix} = L Pe }[/math].
The linear relationship between the mixing time and the Péclet number therefore suggests that the channel length required for mixing to occur increases linearly with the flow velocity. [2] This length to achieve to mixing via diffusion only can become excessively long (>> 1 cm). Thus, it is necessary to incorporate different mixing schemes such that the mixing time becomes less dependent on the Péclet number in order to prevent excessively long channels.
Stokes Flow
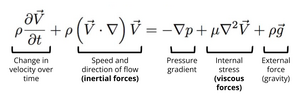
In many microfluidic devices, the Reynolds number is particularly small, where Re << 1. This results in a special kind of laminar flow, where the inertial effects are considered to be negligible and only viscous forces apply. This type of flow is called Stokes flow or creeping flow. Stokes flow is described by Stokes equation, which is a simplified form of the Navier-Stokes equation. The Navier-Stokes equation for an incompressible fluid describes the motion of a Newtonian fluid by taking under consideration the conservation of momentum, the conservation of mass, the density of the fluid ([math]\displaystyle{ \rho }[/math]), pressure ([math]\displaystyle{ p }[/math]), and gravity ([math]\displaystyle{ g }[/math]). The Navier-Stokes equation for an incompressible fluid is shown in Figure 3.
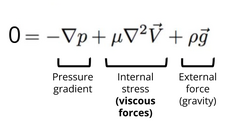
After neglecting the interial terms, the left hand side disappears, and the nonlinear, time-dependent Navier-Stokes equation becomes time-independent and linear with respect to velocity, as shown in Figure 4. Without the dependence on time, the previous history of the flow is not needed to understand the current state of the flow. This means that the behavior of the flow can be predicted simply by knowing the current conditions. Stokes flow is considered instantaneous. The instantaneity of the flow results in reversibility of the flow. [4] For example, imagine some fluid flowing through a channel. The moment a new set of boundary conditions is applied, the flow adjusts accordingly, due to the instantaneity. If the reverse or opposite boundary conditions are then applied, the flow will adjust again and return to its initial state.
A popular demonstration of the reversibility of Stokes flow is the Taylor-Couette experiment, shown in Figure 5. In the Taylor-Couette experiment, dye is injected into a highly viscous fluid that is trapped between two cylinders. When the one of the cylinders is rotated, thereby changing the boundary conditions, the dye moves accordingly (Stokes flow). When the cylinder is rotated back to the starting position, the dye also returns to its initial state, illustrating how Stokes flow is reversible. Therefore, when designing mixers for microfluidic flow, avoiding symmetry is necessary for ensuring mixing occurs.
Mixing on the Microfluidic Scale

Microfluidic systems and devices are becoming more common in a variety of applications and are revolutionizing the biomedical and drug development industries. In standard macroscale systems, mixing is achieved through turbulent flow. Due to the scale of these microfluidic systems, turbulence is not attainable as a result of low Reynolds numbers. Reynolds number is the relationship between inertial forces and viscous forces within a system. [3]
Thus far, several phenomena and mathematical relationships regarding microfluidic mixing have been discussed, and several key points have been developed.
- The amount of time for diffusion to occur is based on the striation length.
- Microfluidic flow is restricted to the laminar region, hence, mixing can only occur through diffusion.
- For microfluidic devices, the length of the channel needed for mixing linearly increases with the velocity of the fluid.
- Since much of microfluidic flow is Stokes flow, the flow is reversible.
Based on these principles, strategies to decrease the striation length, decrease the required channel length, and minimize symmetry must be employed in order to efficiently mix fluids in microfluidic channels. These criteria can be met via the principle of chaotic advection and the understanding of Baker's transformation.
Baker's Transformation
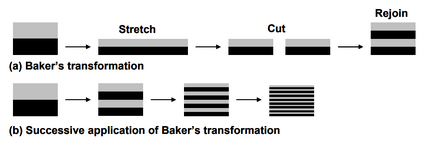
Mixing is a complex phenomena that is not entirely understood, but it can be described as the continuous stretching and folding or breaking and rejoining of fluids. [8] A physical representation of this transformation is mixing play-doh. Suppose you want to mix two different colors of play-doh together, the best way to do so is to stretch and recombine the play-doh layer by layer until the colors are perfectly mixed. This continuous stretching and folding of fluids is known as chaotic mixing or chaotic advection. In this case, the term chaotic means that the flow is sensitive to its initial conditions, and that there is an exponential growth of fluid filaments. [8]
One mathematical explanation of this type of mixing is known as Baker’s transformation, a simple dynamical systems theory. Baker's transformation consists of stretching, cutting, and then rejoining such that the striation length decreases uniformly. Each time the transformation is applied, the striation length decreases by a factor of two, resulting in an exponential decrease in striation length. [2] As a result of decreasing the striation length, the interfacial surface area increases, and thus mixing through diffusion occurs faster. A schematic of Baker's transformation is shown in Figure 7. The time required for mixing to occur can be explained by the following equation, where [math]\displaystyle{ t_{mix} }[/math] is the mixing time and [math]\displaystyle{ t_{adv} }[/math] is time required to transvere one unit of the mixer.
[math]\displaystyle{ t_{mix} }[/math] ~ [math]\displaystyle{ t_{adv} \, log \, Pe }[/math]
In microfluidic flow, however, flow is not easily split and layered. Rather than separating the flow necessary for mixing, microfluidic devices can compartmentalize fluid flow through chaotic advection to enhance mixing.
Chaotic Advection
As a result of chaotic advection, the mixing time only scales logarithmically with the Péclet number instead of linearly, showing that chaotic advection is much more effective than pure diffusion. [2]
As illustrated, chaotic advection is effective at promoting mixing; however, in order for chaotic advection to occur, the flow must have three degrees of freedom. [2] A steady, bounded, two-dimensional flow only has two degrees of freedom, as the constraints of the system generate symmetric flow exhibited by the streamlines aligned in a parallel fashion. [8] This means that fluid flowing through a straight mircofluidic channel cannot experience chaotic advection as chaotic advection requires streamline crossing or asymmetry in the flow. [8] However, through the addition of a third dimension, chaotic advection can be induced. One way is through implementing 3D flow with periodicity in space. More importantly, if 2D flow is made to be periodic in time, the three degrees of freedom criteria is met. [8] Through the implementation of an additional dimension, alternating flow patterns can be generated, which causes periodic velocity that results in chaotic mixing. [1]
It is important to note that despite the stretching and folding of the fluid and the lack of parallel streamlines, the flow still has a low Reynolds number, and it is still considered laminar flow.
Passive Mixing Methods
Passive mixing methods incorporate asymmetric patterns with varied ridges or slanted wells within the microchannels. [1] These unique patterns allow mixing without any added work to the system. Methods such as the Herringbone mixer, twists and bends, recirculating plugs, and droplets are examples of passive mixing methods that use asymmetric patterns.
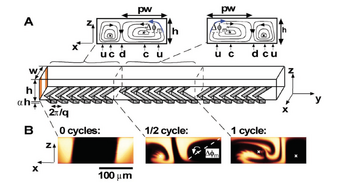
Herringbone Mixer
The Herringbone Mixer is a mixing cycle composed of two sequential ridges in which the direction of asymmetry of the herringbone switches with respect to the centerline of the channel. Resembling the bones of a fish skeleton, its distinctive V-shaped pattern allows for transverse velocity components which induces helical trajectories as seen in Figure 8. An off-centered herringbone pattern can be used to improve the mixing between loops. The fluid can become stretched and folded over itself to reduce the path for diffusional mixing. The Herringbone Mixer can be quantified through the achievable mixing length of the channel, the diffusional length at that position along the channel, and the initial diffusional length. The length of the channel to achieve mixing, [math]\displaystyle{ \Delta y_m }[/math], is
- [math]\displaystyle{ \Delta y_m \sim U \times (\Delta r)^2/D }[/math],
where [math]\displaystyle{ \Delta y_m }[/math] is the length of the channel to achieve mixing, [math]\displaystyle{ U }[/math] is the average linear velocity, [math]\displaystyle{ \Delta r }[/math] is the diffusional length at position [math]\displaystyle{ \Delta y_m }[/math] along the channel, and [math]\displaystyle{ D }[/math] is the diffusion coefficient.
The diffusional length, [math]\displaystyle{ \Delta r }[/math], can be defined as
- [math]\displaystyle{ \Delta r = l \exp(-\Delta y_m /\lambda) }[/math],
where [math]\displaystyle{ l }[/math] is the initial diffusional length (straight channel), and [math]\displaystyle{ \lambda }[/math] is the Liapunov exponent or the characteristic length determined by the geometry of trajectories in chaotic flow.
Therefore, the uniform and homogenous mixing is
- [math]\displaystyle{ \Delta y_m \sim U \times l^2/D = \mathrm{Pe} \times L }[/math].
This can be related to the length for large Peclet number as follows:
- [math]\displaystyle{ \Delta y_m \sim \lambda \ln{(\mathrm{Pe})} }[/math].
In one instance, Stroock et al. fabricated ridges on the bottom of the channel at oblique angles in order to induce transverse flows and therefore induce chaotic advection. [13] The ridges are described to be similar to the rifling in a gun barrel, which present anisotropic resistance to the viscous flow. When the fluid flows parallel to the oblique valleys and peaks, the fluid experiences less resistance than flowing straight through the channel, which is orthogonal to the ridges. These ridges result in tranverse flows, which strech and fold volumes of fluid over the cross section of the channel, ciruculating through the channel. Stroock et al. termed the patterned groves "staggered herringbone mixers" (SHM), in which the asymmetric groove shapes change along the channel. [13] Compared to simple diagonal grooves, these staggered herringbone mixers provide much greater mixing. By changing the orientation of the herringbones every half cycle, the centers of rotation change, resulting in counter-rotating fluid flows, leading to exponential stretching and folding, and thereby further decreasing the striation length and improving mixing.
Twists and Bends
The incorporation of twists and bends can generate chaotic advection as seen in Figure 9. The advection criterion is as follows:
- For square-wave channels, the Reynold’s number must be greater than 70 (Re > 70),
- For a fixed channel length, the Reynold’s number must be equal to 70 (Re = 70),
- For a serpentine mixer, the Reynold’s number must be greater than 6 (Re > 6).
While the square-wave channels allow for 10 times more mixing, the serpentine mixer allows for 16 times more mixing in comparison to the fixed-channel length. The serpentine mixer’s higher characteristic velocity scale allows for the mixer to undergo higher velocity and mixing capabilities than square-wave mixers.
Recirculating Plugs
Recirculating plugs create a plug of one liquid phase that typically contains species to be mixed inside of another immiscible phase. There are no-slip conditions at the walls which forces the liquid inside the plug to move. The liquid-liquid interfaces, where two immiscible liquids meet, are constrained in order to force the liquid to re-circulate. Asymmetry is located at the walls of the channel which induces different sized re-circulating regions. Chaotic advection changes the flow within the drop using the geometry of the channel to mix the content of the drop while maintaining laminar flow.
Droplets
Droplets can move through microfluidic channels while maintaining their original solute concentration within the droplet. Typically, droplets are used to contain multiple reagents or merge droplets containing reactants. It is a challenge to control the rate at which the components mix within the droplets. Without any applied mixing strategies, the components within droplets will mix at the rate of diffusion. A droplet moving within a straight microchannel will use forces generated by movement to create a hemisphereic recirculating flow within the droplet. [11]
The serpentine path assists in the recirculating of flow to improve the mixing relative to diffusion and maintain the areas of low flow. [12] Currently, the most rapid and effective mixing can be achieved by controlling the droplet size and the orientation of bends and patterns in the channel. Step-emulsification, a method to produce monodisperse droplets, uses the geometry present to acheive a high production of droplets. It can offer homogenous droplets with high-dispersed phase ratios as induced by the device geomtrey and interface instabilities.
Bringer et al. were able to induce chaotic advection mixing within droplets. [13] Within a stream of immiscible fluid, they generated fluid plugs and investigated how the geometry of the channel affected mixing. When the plugs flowed through a straight channel, they found that the effectiveness of mixing inside of the plug was sensitive to initial distribution of reagents inside of the plug, meaning that proper distribution of reagents was essential to achieving good mixing. When the plugs flowed through a winding channel, the shearing interaction between the fluid and the walls resulted in periodic recirculation of reagents and thus chaotic advection.
Active Mixing Methods
Active mixing methods incorporate a microfluidic device in which mixing is enhanced in a controllable manner through applied energy disturbance. [1] These devices must be integrated within the microfluidic system and can require external components to operate. Although active mixing methods require the installment of additional components, these mixing methods can be controlled for tuned mixing. Methods such as acoustic micro-mixing, pneumatic valves and mixers, and back and forth mixing are examples of active mixing methods that can comprise of asymmetries.
Acoustic Micro-Mixing
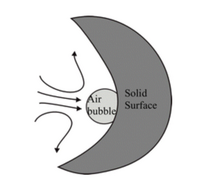
Acoustic Micro-Mixing (AMM) is a method of active mixing which uses sound waves to promote mixing and increase the rate of diffusive mixing. Bubble-induced acoustic micro-mixing uses an air bubble in the liquid as seen in Figure 10.[14] The bubble is then exposed to vibration through sound waves, which generates frictional forces around the bubble and produces strong liquid circulation flow. This method of mixing can also significantly reduce mixing times from 6 hours to 1.75 minutes. This application uses a single apparatus that is easy to implement and has low power consumption which contributes to its low cost. Another advantage of acoustic micro-mixing includes its relatively low strain field. The disadvantages to acoustic micro-mixing consist of the difficulty to fabricate and integrate the device into microfluidic systems. There are limitations to how small the mixing chamber can be in the device. Additionally, the performance of the device is sensitive to bubble size.
Pneumatic Valves and Mixers
Pneumatic valve and mixer systems are another method of active mixing through liquid manipulation on the microfluidic scale. These valves apply pressure to the membrane which actuates liquid flow and are a common type of microvalve controlled by gas pressure.[15] They can be grouped and synchronized to work as pumps or mixers and achieve different forms of liquid flow. This flow method is widely used in microfluidics since it is easy to integrate into different systems.
One of the downsides to these systems is that these microvalves are overly sensitive to the specific device configuration and pressure valves, making their application limited in certain fields. Furthermore, it is important that flow resulting from the use of such valves be carefully designed to stretch and fold the fluids without suffering from the challenge of reversible "back and forth" flow.
Applications of Asymmetric Flow
Achieving mixing within a microfluidic system is essential for a variety of applications, like increasing the rate of reaction. When compared to passive mixing methods, active mixing offers better control over the rate of mixing and the level of mixing. The plethora of active mixers available also provides a suitable option for many different systems. Mixing lipidic mesophases for membrane protein crystallization is an example of asymmetric patterns applied in microfluidic research.
Microfluidics in Lipidic Mesophases for Membrane Protein Crystallization
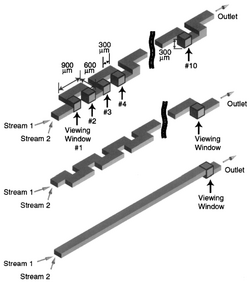
The utilization of asymmetric flow patterns can be observed in the preparation of self-assembling lipid-water mesophases used for crystallizing membrane proteins for structure determination (Figure 11). This mixing strategy was specifically designed to work with small specified volumes of lipid and water, and to address not only the different viscosities of the two starting materials, but also the extreme viscosity and highly non-Newtonian behavior of the resulting mixtures.
Side chambers are asymmetrically arranged to enable offset fluid injection into the center chamber of an integrated microfluidic chip.[15] A tendril-whorl type flow mixing is present at each point of injection in which chaotic mixing is done by stretching and folding the two fluid components until the length scale of the individual lamellae is on the order of the diffusion length. The tendril-type flow occurs as the fluid stretches upon moving from one fluid chamber to another through injection channels. The whorl-type flow occurs as the fluid leaves the injection channels and enters a fluid chamber where it folds around and is enhanced when fluid enters a chamber from multiple injection lines.[15] Note that the fluids used in this study maintain different viscosities.
As shown in Figure 11, the three channels, one in the middle and two on the sides, are arranged asymmetrically. The channels on the sides will squish, allowing for fluid to flow through the middle channel.[15] The purpose of this process is to allow fluids of different viscosities to mix through two separate phases. This type of active mixing strategy is necessary as passive flow strategies involving fluids of different viscosities are very difficult because of flow instabilities.
References
- Ward, K.; Fan, Z. H. Mixing in Microfluidic Devices and Enhancement Methods. J. Micromech. Microeng. 2015, 25 (9), 094001. DOI: https://doi.org/10.1088/0960-1317/25/9/094001
- Kim, S.-G.; Karnik, R.; Kim, J.; Kole, M.; Comeau, B.; Herrick, D. C. Micro/Nano Engineering Laboratory: Microfluidic Mixing https://ocw.mit.edu/courses/2-674-micro-nano-engineering-laboratory-spring-2016/resources/mit2_674s16_microfluidcmix/ (accessed 2022-05-05).
- Squires, T. M.; Quake, S. R. Microfluidics: Fluid Physics at the Nanoliter Scale. Rev. Mod. Phys. 2005, 77 (3), 977–1026. DOI: https://doi.org/10.1103/revmodphys.77.977
- Ouldridge, T. Low Reynolds Number Hydrodynamics: Stokes’ Flow. https://www.imperial.ac.uk/media/imperial-college/research-centres-and-groups/principles-of-biomolecular-systems/Stokes_flow.pdf (accessed 2022-05-05).
- DeMoss, J.; Cahill, K. Laminar Flow. University of New Mexico - Physics and Astronomy, 2007; https://www.youtube.com/watch?v=p08_KlTKP50&ab_channel=UNMPhysicsandAstronomy.
- Kenis, P. J. A.; Ismagilov, R. F.; Whitesides, G. M. Microfabrication Inside Capillaries Using Multiphase Laminar Flow Patterning, "Science", 1999; pp 83-85; DOI: https://doi.org/10.1126/science.285.5424.83
- Ottino, J. M.; Muzzio, F. J.; Tjahjadi, M.; Franjione, J. G.; Jana, S. C.; Kusch, H. A. Chaos, Symmetry, and Self-Similarity: Exploiting Order and Disorder in Mixing Processes. Science 1992, 257 (5071), 754–760. DOI: https://doi.org/10.1126/science.257.5071.754
- Stroock, A. D.; Dertinger, S. K. W.; Ajdari, A.; Mezic, I.; Stone, H. A.; Whitesides, G. M. Chaotic Mixer for Microchannels. Science 2002, 295 (5555), 647–651. DOI: https://doi.org/10.1126/science.1066238
- Liu, R. H.; Stremler, M. A.; Sharp, K. V.; Olsen, M. G.; Santiago, J. G.; Adrian, R. J.; Aref, H.; Beebe, D. J. Passive Mixing in a Three-Dimensional Serpentine Microchannel. Journal of Microelectromechanical Systems. 2000; 9(2), pp 190-197; DOI: https://doi.org/10.1109/84.846699
- Tice, J. D.; Song, H.; Lyon, A. D.; Ismagilov R. F. Formation of Droplets and Mixing in Multiphase Microfluidics at Low Values of the Reynolds and the Capillarly Numbers. Langmuir. 2003; 19, pp 9127-9133 DOI: https://doi.org/10.1021/la030090w
- Bringer, M. R.; Gerdts, C. J.; Song, H.; Tice, J. D.; Ismagilov, R. F. Microfluidic Systems for Chemical Kinetics That Rely on Chaotic Mixing in Droplets. Philos. Trans. A Math. Phys. Eng. Sci. 2004, 362 (1818), 1087–1104. DOI: https://doi.org/10.1098/rsta.2003.1364
- Song, H.; Ismagilov R. F. Millisecond Kinetics on a Microfluidic Cip Using Nanoliters of Reagents. Journal of the American Chemical Society. 2003; 125, pp 14613-14619 DOI: 10.1021/ja0354566
- Liu, R. H.; Yang, J.; Pindera, M. Z.; Athavale, M.; Grodzinski, P. Bubble-induced acoustic micromixing. "Lab on a Chip". 2002; 2, pp 151-157; DOI: https://doi.org/10.1039/B201952C
- Lau, A. T. H.; Yip, H. M.; Ng, K. C. C.; Cui, X.; Lam, R. H. W. Dynamics of Microvalve Operations in Integrated Microfluidics. Micromachines. 2014; 5, pp 50–65; DOI: 10.3390/mi5010050
- Perry, S. L.; Roberts, G. W.; Tice, J. D.; Gennis, R. B.; Kenis, P. J. A. Microfluidic Generation of Lipidic Mesophases for Membrane Protein Crystallization. Crystal Growth & Design. 2009; 9(6), pp 2566-2569; DOI: https://doi.org/10.1021/cg900289d
