Stokes Flow - Samrat Sur
content
Definition Derivation references
Definition
Stokes flow, also named creeping flow or creeping motion, is a type of fluid flow where advective inertial forces are small compared with viscous forces. This is a type of laminar flow, where streamlines are parallel to each other as shown in Figure 1 and the Reynolds number, Re<<1 [1,2]. The dimensionless number used to define the ratio of the advective to viscous forces is know as Reynolds number, Re. Reynolds number is given by the following relation:
- [math]\displaystyle{ \mathrm{Re} = \frac{\rho U L}{\mu} }[/math]
where,
- [math]\displaystyle{ \rho }[/math] is the density of the fluid (SI Units: kg/m3)
- U is the velocity of the fluid (SI Units: m/s)
- L is the characteristic length of the fluid. This varies depending on through what the fluid is flowing (SI Units: m)
- [math]\displaystyle{ \mu }[/math] is the dynamic viscosity of the fluid (SI Units: Ns/m2)
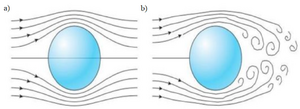
While, for higher Reynolds number, Re>>2000, the flow transitions into a turbulent flow and becomes chaotic. Also, another important aspect of Stokes flow is that it is time reversible. Experimental investigations have shown that mixing in laminar flow regime can be reversed to approximately the initial state [3]. In microfluidics devices, the Reynolds number is small (often on the order of unity or smaller) or at least not so large that the convective terms of the Navier Stokes equations are important [4-7]. For example, in a channel with height 100 microns, a flow with water of viscosity of [math]\displaystyle{ \mu }[/math]=0.001Pa.s at a typical speed of U=0.01 m/s has a Reynolds number of unity. Thus the convective term in the Navier Stokes equation can be neglected, which removes the non-linearity from the equation and this flow in a microfluidic channel can be solved for incompressible fluids with no slip boundary conditions. To better understand the linearizing of the Navier Stokes equation we need to non-dimensionalize the Navier Stokes equation.
Derivation
The Navier Stokes equation is given by :

Where the terms on the left side is the rate of change of momentum of the fluid element and the terms on the right represents the forces acting on the fluid element. The left side of the equation represent the inertial terms and the right side of the equation represents the force term, such as viscous forces, hydrostatic and body forces.
In order to do understand the effect of neglecting inertial effects and to derive the Stokes equation we need to represent all the physical variable of the Navier-Stokes equation defined for a microfluidic system shown in Figure 1 in terms of either a "characteristic scale" or "characteristic scales".
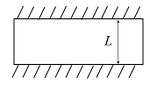
Now normalizing the variables in equation 1 by the dimensionless quantities,
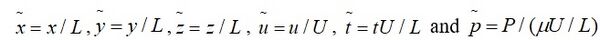
where, P is the characteristic pressure, U is the characteristic velocity, L is the characteristic length, and all the terms with ~ represents the dimensionless variables. Next, we need to substitute these dimensionless variables into equation 1.1 which yields the following relation,
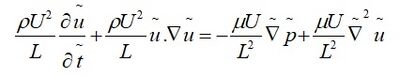
Simplifying the equations further, we get,
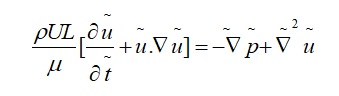
Where [math]\displaystyle{ \mathrm{Re} = \frac{\rho U L}{\mu} }[/math], is defined as the Reynolds number, Re. Thus in the case of flow in microfluidics devices, where we have shown that Re<<1, we can thus neglect the left side of the equation, which is the Stokes equation a shown in equation 1.3
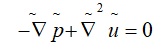
Here it is interesting to note that, for a pressure driven flow, the characteristic pressure scaling for a can be derived for different flow regimes from the Navier Stokes equation through a simple scaling analysis as shown below. For a high Reynolds number regime, where inertial effects are dominant, the characteristic pressure scales as
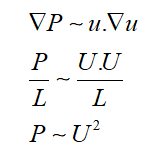
Whereas for the case of low Reynolds number regime flow, the pressure scales as,
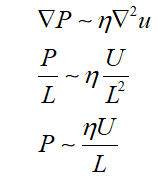
Similarly, another way look at Reynolds number would be to look in terms of time scales. We can rewrite the Reynolds number as,
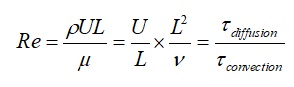
Where [math]\displaystyle{ \mu }[/math], is the kinematic viscosity, [math]\displaystyle{ \tau (diffusion) }[/math] and [math]\displaystyle{ \tau (convection) }[/math] are the timescales for diffusion and convection. Thus in Stokes flow, where Re<<1, the diffusion time scale is much smaller as compared to convective time scale and thus viscous effects are dominating. Whereas, for Re>>1, the convective time is much faster as compared to the diffusion and thus inertial effects become dominant.
References
[1] "https://aapt.scitation.org/doi/abs/10.1119/1.10903", Purcell, E.M., ‘‘Life at low Reynolds number,’’ American journal of physics 45, 3-11 (1977).
[2] "https://openwetware.org/wiki/Reynolds_Number_(Re)_-_Blayne_Sarazin"
[3] "https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.77.4170", Flekkøy, E., T. Rage, U. Oxaal, and J. Feder, ‘‘Hydrodynamic irreversibility in creeping flow,’’ Physical review letters 77, 4170 (1996).
[4] "https://www.annualreviews.org/doi/abs/10.1146/annurev.fluid.36.050802.122124Stone" , H.A., A.D. Stroock, and A. Ajdari, ‘‘Engineering flows in small devices: microfluidics toward a lab-on-a-chip,’’ Annu. Rev. Fluid Mech. 36, 381-411 (2004).
[5] "https://www.ncbi.nlm.nih.gov/pmc/articles/PMC1233830/" Brody, J.P., P. Yager, R.E. Goldstein, and R.H. Austin, ‘‘Biotechnology at low Reynolds numbers,’’ Biophysical journal 71, 3430-3441 (1996).
[6] "https://pubs.acs.org/doi/abs/10.1021/la030090w" Tice, J.D., H. Song, A.D. Lyon, and R.F. Ismagilov, ‘‘Formation of droplets and mixing in multiphase microfluidics at low values of the Reynolds and the capillary numbers,’’ Langmuir 19, 9127-9133 (2003).
[7] "https://royalsocietypublishing.org/doi/pdf/10.1098/rsta.2003.1355" Ottino, J.M. and S. Wiggins, “Introduction: mixing in microfluidics,” in Editor (ed)^(eds). Book Introduction: mixing in microfluidics (The Royal Society, 2004).
