Droplet Microfluidics: Mixing within Droplets - Edward Esposito

Background

Figure 1: Highlights generation of a droplet with different reagents³. Reprinted with permission from {Langmuir 2003 19 (22), 9127-9133, DOI: 10.1021/la030090w}. Copyright {2003} American Chemical Society.

Along with a number of benefits that arise from working in the microscale, including working in a laminar flow regime, there are some novel problems. Two such problems are sample dispersion and mixing. There have been many microfluidic devices designed to improve mixing, and similar efforts to control dispersion. One of the most effective means of controlling dispersion is to isolate the aqueous phase in an immiscible carrier fluid (in some cases the reactants, or molecules of interest, may be in the non-aqueous phase). These droplets, or plugs, can be generated in uniform size, and moved through microfluidic channels with relative ease, and the solute concentration can remain unchanged within the droplet. For many applications, however, we need to combine multiple reagents, and often in a time-sensitive manner, with complete mixing. In these cases, it is useful to create droplets that contain multiple reagents, or merge droplets containing reactants. For a discussion on generation of, or merging of, droplets please refer to the pages on Merging Droplets and T-Junctions. While droplets resolve the issue of dispersion, it creates a unique mixing problem.

Once droplets have been created or merged within a microfluidic channel, the rate at which their components mix within the droplets may need to be controlled, specifically in cases where rapid mixing is required (Figure 1 shows an example of a formed droplet with reagents that need to be mixed). Some examples of where rapid mixing is important include explorations of reaction kinetics or the study of thermal events resulting from molecular interactions. For the purpose of this discussion, we will treat merged droplets, where multiple droplets containing unique reagents are combined, and droplets, containing a number of reagents introduced during the formation of the droplet, in a similar manner. Regardless of how the components came to be in the droplet at a space in time, true also for a product that is formed within a droplet, one may need to completely mix all components within a droplet more rapidly than is possible by diffusion.

Approaches

Figure 2: Image reprinted with permission from (Angew. Chem. Int. Ed., Volume: 45, Issue: 44, Pages: 7336-7356, First published: 06 November 2006, DOI: (10.1002/anie.200601554) )⁷ describing the folding and stretching similar to that which occurs in a droplet traversing a bend in a microfluidic channel.

Without any applied mixing strategy, components will mix within droplets or immiscible-plugs at the rate of diffusion¹. This is also true in cases where immiscible reactants are used to form reaction interfaces². In the latter case, products would remain at the interface longer without some mechanism of moving the product from the interface more rapidly. In each case, flow within the droplet can be affected by many variables of the microfluidic system. When a droplet moves within a straight microchannel, the forces generated by movement create a hemispheric recirculating flow within the droplet³. Factors that affect the rate of mixing within the moving droplet are; position of the reagents at the start, the capillary size, the droplet/capillary ratio, the flow rate of the introduced droplet material, and the flow rate of the carrier fluid^2,4,5. The Reynolds number has a small effect on the process. This recirculating flow greatly improves mixing relative to diffusion but maintains areas of low flow (or “dead spots”) and was improved upon by introduction of a serpentine pattern to the flow path⁶.

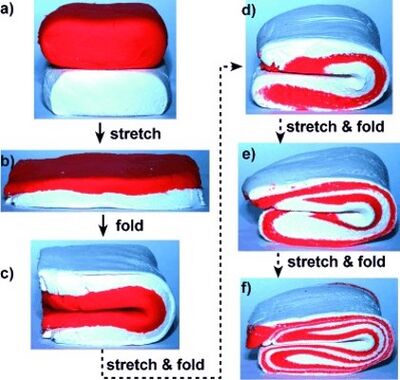
To date, it appears the most rapid and effective mixing can be achieved by controlling the droplet size, relative to the capillary size, and incorporation of bends, or a serpentine pattern, in the channel. The optimal droplet size is roughly 1-2 times the channel height. Incorporation of an alternating path direction, such as a bend or serpentine pattern, has the advantage of folding and stretching the droplet, while the straight paths generate recirculating flow within halves of the droplet. This stretching and folding effect, also referred to as the Baker’s Transformation because it resembles the kneading and folding that a baker would use with dough, was well diagrammed in a review by Song ⁷ and described in Figure 2. The combined effects of recirculating flow and Baker’s Transformation serve to generate chaotic flow and rapidly mix the contents within the droplets.

Viscosity differences within droplets and the effects on mixing

Many of the solutions used in microfluidic devices will be of high concentration and may contain additives, like polyethylene glycol, which will significantly their viscosity relative to water or dilute buffers. Some examples of these higher viscosity solutions are samples for crystallization studies, and enzyme stocks for high throughput activity assays used in drug screening. As one might expect, the viscosity of components in the aqueous phase can play a role in both the formation of droplets and mixing within droplets. The focus here will be on the mixing within the droplets.

Tice et al. have demonstrated that mixing within droplets formed from reagents of different viscosity still occurs via recirculating flows⁴. Counter to expectations, they observe that for many conditions the mixing speed with reagents of dissimilar viscosity was faster than for reagents of similar viscosity. This is likely due to the disruption of lamina that persist in a hemispherical recirculating flow. Additionally, they showed that deliberate placement of higher viscosity material to the front or back of a droplet resulted in greater disruption to the recirculating pattern and thus faster mixing time; this is especially important when forming longer plugs (>2x capillary height).

Cases in literature

Figure 3: (A) Drawing describing the recirculating flow described in². Here we highlight the organic fluid area where the nitrated product was formed. It is reasonable to assume there is some recirculating flow in this plug as well, but the flow pattern is expected to be unique relative to that in the larger plug modeled in the text. (B) Drawing describing the laminar reactor described in Burns and Ramsahw

In 2003 there were several papers from the Ismagilov group highlighting opportunities available with the use of immiscible droplets in microfluidic devices. One noteworthy paper is the work of Song et al. who demonstrated successful measurement of millisecond kinetics by taking advantage of the rapid mixing of reagents in multiphase flow ⁶. This work was completed in a device with a serpentine channel, described earlier, where it was determined that mixing was complete in 2 milliseconds⁸. These experiments were performed using sub microliter volumes of reagent, offering a very large reduction in sample volume compared to the state-of-the-art at the time, stopped-flow and quench-flow devices, which required hundreds of microliters of reagents. Specifically, they determined the catalytic turnover rate of Ribonuclease A using 150 nL of reagent for each complete measurement, and the measurement time was on the order of 4 seconds.

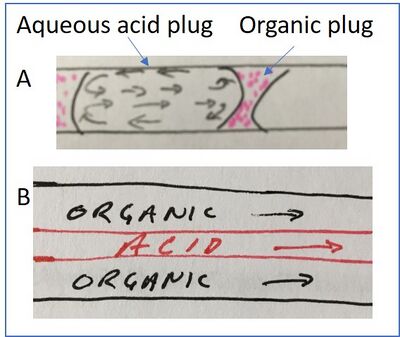
Dummann et al. utilized a two-phase liquid-liquid capillary system as a microreactor, taking advantage of the high heat transfer rates afforded by the microscale system to perform highly exothermic reactions in essentially isothermal conditions². They were enabled to perform detailed mechanism of reaction analyses that would otherwise have been more challenging. Because microfluidic systems utilize such low reagent volumes and have relatively large surface area contact with the surroundings (the channel here) they were able to study activation energies of nitration reactions at defined temperatures when the strongly exothermic reaction would normally raise the temperature of the system. Additionally, they were able to exploit the high mass transfer rates, that result from flow in microcapillaries, to demonstrate the mechanism of action of by-product formation. Ultimately, they were able to produce higher purity product and eliminate one class of by-product completely. In their system, the nitration acid was present in the aqueous phase, the aromatic reagent to be nitrated was in the organic phase, and the reaction took place at the phase interface. As product was generated, the recirculating flow within the plugs would, effectively, sweep away the product before a subsequent nitration could occur. Curiously, they produced CFD modeling data to support the conclusion that by-product was reduced by high mass transfer generated by circulating flow in the aqueous phase, but the sequential by-product reaction with aromatics occurred in the organic phase. One could reason that there is recirculating flow in the organic phase as well, but this was not highlighted; in the case of the organic phase, there would be a unique interface, described in Figure 3, resulting from the lower surface tension relative to aqueous solvent. The benefit of using droplets, or plugs, in this multiphase microreactor is highlighted when compared to the work of Burns and Ramshaw, who performed a similar reaction in a laminar flow microreactor where the product, by design, would persist at the interface⁹. Because product in the laminar flow microreactor remained at the acid interface, it could be subsequently nitrated, forming unwanted byproduct.

In the work described above, Dummann took advantage of the high heat flow to perform strongly exothermic reactions in essentially isothermal conditions, and Song took advantage of the extremely rapid mixing that could be obtained using a winding channel. Recently, a group at the Palo Alto Research Center developed an optical microcalorimeter that partitions reactants in aqueous droplets within an immiscible carrier fluid^10,11; a microcalorimeter measures small heat changes, like those associated with biomolecular binding events. This is especially interesting, and challenging, considering the work described above, because an optical calorimeter requires measurement to be made before this small amount of heat is lost to the surroundings (the carrier fluid and the chip), and, therefore, requires very rapid mixing and measurement. In their system, they attempt to measure the heat of binding between two small molecules, calcium ion and ethylenediaminetetraacetic acid (EDTA), at low concentration (mM reaction concentrations vs. M or neat reagent in the microreactor). This reaction produces little heat (~10 kJ/mol), about 10X less compared to the nitration reaction described above (~150 kJ/mol), so poses a tremendous challenge to balance between allowing sufficient time to adequately mix the reagents and completing the measurement before the reaction heat is lost. Remarkably, the authors demonstrate the ability to measure the reaction heat of relatively dilute solutions in 900 pL droplets using wavelength shifts of thermochromic liquid crystals (TLCs) as the readout.

Commercial applications and solutions

Because of the limited quantities produced by capillary microreactors, it may limit commercial use as a research tool for investigating reaction mechanisms to better understand the development of large-scale manufacturing processes. That said, parallel microreactors with capability for precise control of reaction chemistry present unique opportunity in the field of medicinal chemistry.

One area where our understanding of mixing in droplets has provided opportunity in applied use is the next generation sequencing (NGS) field. Droplet sequencing (Drop-seq) is used in single cell sequencing and can be performed with ready-made reagents from Illumina and can be analyzed on instruments from Illumina and, more recently, Dolomite-bio. This technique relies on rapid droplet mixing in multiple phases of the sequencing process. When droplets are generated to contain barcoded oligos and lysis reagents they need to be mixed rapidly to enable the processing of the large numbers of cells needed to obtain reasonable population statistics. The value in single cell sequencing comes from the ability to understand population variation, for example in identifying genetic variation in evasive tumor cells. Single cell sequencing was recognized by Nature Methods as the Method of the Year in 2013¹².

References

1 K. Handique and M. A. Burns, Journal of Micromechanics and Microengineering, 2001, 11, 548-554 (DOI:10.1088/0960-1317/11/5/316).

2 G. Dummann, U. Quittmann, L. Gröschel, D. W. Agar, O. Wörz and K. Morgenschweis, Catalysis Today, 2003, 79, 433-439 (DOI:10.1016/S0920-5861(03)00056-7)

3 J. D. Tice, H. Song, A. D. Lyon and R. F. Ismagilov, Langmuir, 2003, 19, 9127-9133 (DOI:10.1021/la030090w)

4 J. D. Tice, A. D. Lyon and R. F. Ismagilov, Analytica Chimica Acta, 2004, 507, 73-77 (DOI:10.1016/j.aca.2003.11.024)

5 M. N. Kashid, I. Gerlach, S. Goetz, J. Franzke, J. F. Acker, F. Platte, D. W. Agar, and S. Turek, Ind. Eng. Chem. Res. 2005, 44, 5003-5010 (DOI:10.1021/ie0490536)

6 H. Song and R. F. Ismagilov, Journal of the American Chemical Society, 2003, 125, 14613-14619 (DOI:10.1021/ja0354566)

7 H. Song, D. L. Chen and R. F. Ismagilov, Angewandte Chemie International Edition, 2006, 45, 7336-7356 (DOI:10.1002/anie.200601554)

8 H. Song, J. D. Tice and R. F. Ismagilov, Angew. Chem. Int. Ed. 2003, 42, 767 (DOI:10.1002/anie.200390203)

9 J. R. Burns and C. Ramshaw, Chemical Engineering Research and Design, 1999, 77, 206-211 (DOI:10.1205/026387699526106)

10 J. Chamoun, A. Pattekar, F. Afshinmanesh, J. Martini and M. I. Recht, Lab on a chip, 2018, 18, 1581-1592 (DOI:10.1039/C7LC01266G)

11 M. I. Recht, J. Chamoun, A. Pattekar, and J. Martini, Proc. SPIE 10895, Frontiers in Biological Detection: From Nanosensors to Systems XI, (DOI:10.1117/12.2511764)

12 Nature methods, 2014, 11, 1 (DOI:10.1038/nmeth.2801)