Péclet number (Pe) - Nishanth Saldanha
Definition
The Péclet number (Pe) is a dimensionless number that represents the ratio of the convection rate over the diffusion rate in a convection-diffusion transport system. [1][2]
[math]\displaystyle{ Pe = \frac{(Convection \, rate)}{(Diffusion \, rate)} = \frac {UL}{D} }[/math]
U represents linear flow velocity in the control volume, L represents the length scale of the flow and D is the diffusion constant. This number can also be represented as a ratio of diffusive to convective time scales. The units, in a microfluidic setup, for U, L and D are μm/s, μm/s and μm2/s respectively.
[math]\displaystyle{ Pe = \frac{(Diffusion \, timescale)}{(Convection \, timescale)} }[/math]
In diffusion dominated regimes, the Péclet number is less than 1. Such is the case with microfluidic systems, where turbulence is low. In convection dominated systems, this number is greater than one.
Derivation [3]
For a one dimensional system as described in Figure 1, with a species concentration, [math]\displaystyle{ C }[/math] following relations can be made to relate flux in, [math]\displaystyle{ J_{in} }[/math] , flux out, [math]\displaystyle{ J_{out} }[/math] and control volume [math]\displaystyle{ V }[/math]. From this system, the Péclet number can be derived.
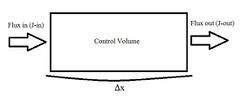
[math]\displaystyle{ V\frac{dC}{dt} = A\cdot J_{in} - A\cdot J_{out} }[/math]
This mass balance can be used to describe the flux into and out of the system. Flux is mass flow rate per unit area. Assuming inlet and outlet areas are constant, the mass balance can be simplified.
[math]\displaystyle{ \frac{dC}{dt} = \frac{A}{V}\cdot (J_{in} - J_{out}) }[/math]
If there are gradients in the system, the flux out of the system can be described as follows.
[math]\displaystyle{ J_{out} = \frac{\partial J}{\partial x}\cdot (\Delta x)+J_{in} }[/math]
Thus, the mass balance can be simplified as shown below.
[math]\displaystyle{ \frac{dC}{dt} = \frac{A}{V}\cdot \frac{\partial J}{\partial x}\cdot (\Delta x) }[/math]
Due to how the system is defined, [math]\displaystyle{ \frac{A}{V} = \frac{1}{\Delta x} }[/math]. Thus,
[math]\displaystyle{ \frac{dC}{dt} = \frac{\partial J}{\partial x}\rightarrow \frac{\partial C}{\partial t} =\nabla J }[/math]
This equation is also described in three dimensions.
The assumption of negligible sources and sinks are made, so as to focus the system on diffusion and convection. Thus,
[math]\displaystyle{ J = J_{convection} + J_{diffusion} }[/math]
Mass flow rate, [math]\displaystyle{ Q }[/math], can be defined as [math]\displaystyle{ Q = C \Delta x\cdot A }[/math]. Since the convection is the prime source of this mass flow rate in this system, convective flux, [math]\displaystyle{ J_{convection} }[/math] is defined as such.
[math]\displaystyle{ J_{convection} = \frac{Q}{\Delta t\cdot A} = \frac{C \Delta x }{\Delta t} \rightarrow \frac{\partial x}{\partial t}C }[/math]
Diffusion equation can be derived from first Fick's law as shown below. [math]\displaystyle{ D }[/math] is the Diffusivity constant.
[math]\displaystyle{ J_{diffusion} = -D \frac{\partial C }{\partial x} }[/math]
Diffusive flux and Convective flux can be combined into the overall mass balance.
[math]\displaystyle{ \frac{\partial C}{\partial t} = -\frac{\partial \left [ J_{convection}+J_{diffusion} \right ]}{\partial x} = -\frac{\partial \left [ \frac{\partial x}{\partial t}C + -D \frac{\partial C }{\partial x} \right ]}{\partial x} }[/math]
Because the relation below can be applied, where [math]\displaystyle{ u }[/math] equals velocity of a particle, the mass balance can be simplified and described in multiple dimensions
[math]\displaystyle{ \frac{\partial x}{\partial t} = u }[/math]
[math]\displaystyle{ \frac{\partial C}{\partial t} = D\frac{\partial^{2} C}{\partial x^{2}} - u \frac{\partial C}{\partial x}\rightarrow \frac{\partial C}{\partial t} + u \frac{\partial C}{\partial x}= D\frac{\partial^{2} C}{\partial x^{2}} \rightarrow \frac{\partial C}{\partial t} + u \nabla C= D \nabla^{2} C }[/math]
Dimensionless numbers, as shown below can be used to restate the mass balance. [math]\displaystyle{ U }[/math] equals the convective linear flow rate.
[math]\displaystyle{ C^{*} = \frac {C}{C_{max}}; U^{*} = \frac{u}{U}; t^{*} = \frac {t}{t_{0}} }[/math]
When these numbers are applied, the balance is described as shown.
[math]\displaystyle{ \frac{C}{t_{0}}\frac{\partial C^{*}}{\partial t} + \frac{UC}{L}u^{*} \frac{\partial C}{\partial x}= \frac{DC}{L^{2}}\frac{\partial^{2} C}{\partial x^{2}} }[/math]
[math]\displaystyle{ \frac{L^{2}}{D\cdot t_{0}}\frac{\partial C^{*}}{\partial t} + \frac{UL}{D}u^{*} \frac{\partial C}{\partial x}= \frac{\partial^{2} C}{\partial x^{2}} }[/math]
The first term in the above balance is referred to as the unsteady term. In time invariant flows, this term equals zero. The ratio between the remaining two terms (i.e. the diffusive and convective terms), equals the Peclet number, as described below.
[math]\displaystyle{ Pe = \frac {UL}{D} }[/math]
Applications to Microfluidics
The low inertial forces present within many microfluidic setups, due to low velocity and length scales, often yield low Reynolds number flows. [4] Low levels of turbulence can also be expected in these flow regimes. Thus convection is not prevalent in microfluidic setups unless it is purposely induced. The mixing that does occur in these devices occur due to diffusion. [4] Diffusion induced mixing is much slower than convective mixing, with speeds lower by several orders of magnitude. [4]
In units where quick mixing is not desired (for example, analytical tests or separation systems), low Pe (of less than or around 1) is ideal. T-sensors, as shown in Figure 2, are an example of a class of analytical devices that benefit from low Pe. T-sensors are used in many competitive immunoassays, where antigen and antibody are input into the T-sensor. Given the known diffusion patterns that are expected, as shown in Figure 2, any deviation from this pattern indicate antibody binding. T-sensors can also be used in simpler cases, such as to quantify the diffusivities of the analyte and reaction kinetics since the effects of turbulence are neutered [4]. Separation is also possible without the use of membranes in microfluidics, due to low Pe, as evidenced by the H filter. H-filter takes advantage of the fact that larger species have lower diffusion constants than smaller species. Proteins, for example, have diffusion coefficient three orders of magnitude larger than that of salt ions. [3] Separation can be achieved in a 'H' shaped channel, where a mixture will enter on the ends of the 'H' and a separation will occur such that the larger species will exit the bottom of the same side, while the lighter species will traverse the middle section of the H onto the other side.
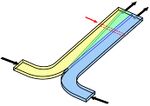
In units where mixing is desired, such as reactors, Pe>>1 is necessary. Convection desired to produce large Pe can be provided with many methods such as using stir bars or using etched channels that induce vortices, as shown in a herringbone mixer in Figure 3.
References
[[1]] MIT OpenCourseWare. Transport Processes In The Environment. Nepf, H. 2008. https://ocw.mit.edu/courses/1-061-transport-processes-in-the-environment-fall-2008/
[[2]] Bergman, C.; Lavine, A.; Incropera, F.; DeWitt, D. Fundamentals of Heat and Mass Transfer, 7th ed. Wiley, 2011. https://www.wiley.com/en-us/Fundamentals+of+Momentum,+Heat,+and+Mass+Transfer,+7th+Edition-p-9781119495413
[[3]] Lagoon Ecosystem Modelling (ECOPATH/ECOSIM): From Hydrodynamics to Fisheries. Derivation of Basic Transport Equation, 2011. https://www.io-warnemuende.de/files/project/amber/workshops/Lagoon%20Ecosystem%20Modelling/SSK-Lecture4.pdf
[[4]] Squires, T.; Quake, S. Microfluidics: Fluid physics at the nanoliter scale. Rev Mod Phys. 2005, 77 (3), 977-1026. DOI: https://doi.org/10.1103/RevModPhys.77.977
[[5]] " Schilling, E.; Kamholz, A.; Weigl, B. The T-sensor. http://faculty.washington.edu/yagerp/microfluidicstutorial/tsensor/tsensor.htm (accessed Feb 26, 2022).
[[6]] MIT OpenCourseWare. Design and Fabrication of Microelectromechanical Devices. Livermore, C.; Voldman, J. 2008. https://www.flickr.com/photos/mitopencourseware/3490710123/in/photostream/
