Herringbone Mixers - Jun-Goo Kwak

Introduction

Typical flow within microfluidic channels is laminar, in addition, the timescale of molecular diffusion within these devices is more often than not slow. However, for many applications of microfluidics which includes various detections and analyses, mixing of fluids is of critical importance. Physically, within the small channels of microfluidic devices, flow is laminar given a low Re < 100. Laminar flow is characterized by sufficiently low velocities that adjacent fluid streams travel past one another in an orderly fashion. Thus, the predominant mechanism for transport is passive diffusive mixing. To relate molecular diffusion and convection, the Péclet number is defined as:

[math]\displaystyle{ \mathrm{Pe} = \dfrac{ \mbox{advective transport rate} }{ \mbox{diffusive transport rate} } }[/math]

For mass transfer, it is defined as:

[math]\displaystyle{ \mathrm{Pe} = U \times L/D }[/math]

where L is the characteristic length, U the local flow velocity, D the mass diffusion coefficient. Thus, the length scale required for uniform and homogenous mixing can be derived using the Péclet number:

[math]\displaystyle{ \Delta y_m \sim U \times L^2/D = \mathrm{Pe} \times L }[/math]

For most microfluidic devices, this results in length scales >> 1 cm. Therefore, due to the linear scaling of the distance required with increasing Pe, microfluidic devices quickly become prohibitively larger in order to achieve mixing simply through diffusion. To constrain devices within the same length scale, different mixing schemes can be utilized to mix fluid within the channel itself without any active components. First introduced by Stroock and Whitesides, Herringbone mixers rely on the principle of stretching and folding transverse volumes of fluid over the cross-section of the microfluidic channel to reduce the mixing length. As transverse flows are generated, the average distance for diffusion to occur along this axis is decreased to homogenize unmixed volumes.

Generating Transverse Flows

Figure 1 a) Schematic representation of herringbone mixture with twisting flow in the channel. b) Brightfield image showing red and green dyes undergoing mixing. c.) Fluorescent confocal images of the cross section of the channel showing rotation at different points within the channel.

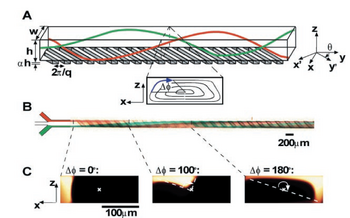
Transverse flows can be generated in the following manner as shown in Figure 1. Ridges are first fabricated out of PDMS using a simple two-step photolithographic procedure at an oblique angle to the long axis, y. For flows traveling along the y axis, these ridges provide anisotropic resistance. Thus, for viscous flows with low Re, resistance encountered by the fluid is much less in the y' axis compared to the orthogonal direction along the x' axis. Due to the anisotropic resistance to flow, a pressure gradient is formed at the origin of the ridge, creating transverse flow in the x' direction which then subsequently recirculates in the -x' direction.

Staggered Herringbone Mixers

To increase the efficiency of herringbone mixers, chaotic flow can be introduced by adding both rotational and extensional local flows sequentially. To achieve this, the ridges can be placed as a function of the axial length of the microfluidic chip with alternating orientation as shown in Figure 2.

Figure 2 a.) Schematic showing mixing cycles due to the assymetry of the chevrons within the staggered herringbone device. Centers of rotation are indicated by "c", where areas of upwelling and downwelling are labeled by "u" and "d" respectively. b.) Fluorescent confocal images showing mixing after half and a full cycle

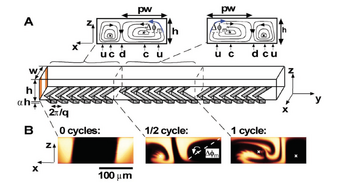
By adjusting the orientation of the ridges in alternating sequence such that they are asymmetric with respect to the centerline of channel, the centers of rotational flow ("c") and up- and down-dwellings ("u" and "d") are further exchanged, improving the efficiency of mixing.

Importantly, this mixing efficiency is a function of two parameters: p, a measure of the asymmetry of the herringbones, and Δφ, a measure of the amplitude of the rotation of the fluid per half cycle which is dependent upon the number of herringbones per half cycle. If p goes to 1/2, or perfect symmetry or Δφ goes to zero, the flow becomes nonchaotic reducing efficiency. To maintain optimal mixing, p = 2/3 and Δφ > 60°.

This steady chaotic transverse flow results in a dramatic reduction in the length scale necessary to achieve uniform mixing. Given that the average distance over which diffusion must occur is Δr, the stretching and folding of volumes of fluid is described by an exponential function relating the characteristic length,

[math]\displaystyle{ \Delta r = l \exp(-\Delta y/\lambda) }[/math]

where where l is the initial transverse distance taken and λ is the characteristic length of the geometry of trajectories in the chaotic flow. This can be related to the length as follows:

[math]\displaystyle{ \Delta y_m \sim \lambda \ln{(\mathrm{Pe})} }[/math]

This resultantly drives down the length scale to such that it grows only logarithmically with respect to the Péclet number.

Applications of Herringbone Mixers

Herringbone mixers have been utilized in a variety of different microfluidic platforms. One emerging area is their use in the development of microfluidic devices for medical diagnostics such as cancer. Cancer is the second leading cause of death in the United States. While the 5-year survival rate for most cancers is relatively high for most primary cancers, this precipitously drops as the cancer spreads and metastasizes, accounting for >90% of cancer deaths.

Isolation of CTC from Whole Blood

Figure 3 a.) Herringbone mixer with uniform blood flow throughout the device. b.) Brightfield image and schematic showing periodicity and asymmetry of the chevrons. c-d.) Cartoon depicting cells in the various streamlines of each device. e.) flow visualization showing microvortices due to the grooves of the herringbone structure. f.) flow visualization of laminar flow.

Figure 4 Immunohistochemistry image of a CTC cluster isolated from a prostate cancer patient using the herringbone chip.

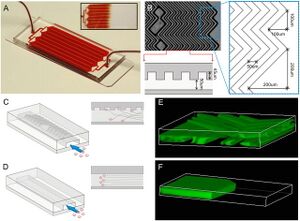
Circulating tumor cells (CTC) in peripheral blood from cancer patients have not only recently been identified as the origin of disseminated tumor cells in vital organs, but also are recognized to serve as an early biomarker for cancer diagnosis. One critical challenge to the study of CTC is their extremely low frequency, (≤1 CTC/mL of blood), resulting in their limited clinical utility.

Microfluidic devices offer advantages over other cell purification techniques such as (i) efficient processing of complex fluids, (ii) minimal damage to cells and (iii) ability to support live cells. One critical limitation of using microfluidic devices with uniaxial and laminar flow for cell capture is that cells follow streamlines. This is critical in capturing cells based on antibody-coated surfaces as this decreases the number of interactions possible between the cells and the antibody used, reducing the chance for cell capture.

To overcome this challenge, Stott et al. under the guidance of Mehmet Toner utilized herringbone mixers to generate microvortices to direct cells towards antibody-coated surfaces as shown in Figure 3. Herringbone mixers have simple geometry which makes them amenable to large-scale manufacturing as collisions between target cells and antibody-coated surfaces are maximized without the need for complex structures. In addition to increased CTC capture efficiency, the design of this device allows for higher blood volume throughput and is amenable to traditional optical imaging techniques due to its transparency.

Development of such devices that interface with existing technologies such as histopathology platforms enable for the development of new platforms. In this case, the ability to collect significant numbers of CTC in a high-throughput manner allows for the possibility of broader application in cancer diagnostics and realize the potential of a "blood biopsy" point-of-care device.

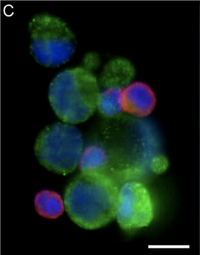
Interestingly, this herringbone device allowed for the isolation of CTC clusters from prostate cancer patients that have not been previously observed as shown in Figure 4. Previous batch separation techniques and laminar flow microfluidic devices prevented their observation. Thus, the existence of such clusters may provide new insight into the fundamental mechanisms of metastasis, as current knowledge and understanding is derived exclusively from animal models in which a single cell extravasates and colonizes a distal site.