Droplet Microfluidics: Recirculating Liquid Plugs in Droplets - Sam Marsden
Introduction
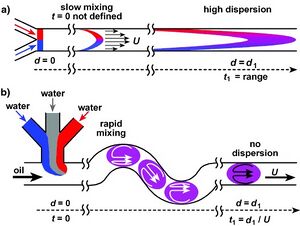
In macro-scale systems it can be easy to mix up a solution; one can use methods like dispersion or agitation to completely mix them. However, on the micro-scale it is not that easy. With a small channel size in microfluidic systems, the Reynolds Number is very small so the viscous forces dominate over inertial forces. Because of this, through droplet microfluidics we can create plug flow systems in which “plugs” of capsular droplets or bubbles with the effective diameter of the channel individually flow[1]. We can then use the geometry of the channel to mix the plug composition through chaotic advection, producing totally mixed droplets at the outlet. This allows us to have rapidly mixed solutions with no dispersion along the channel[2].
Underlying Principles
Passive Mixing
Due to the low Reynolds Number, microfluidic devices exhibit laminar flow. This ordered flow makes it difficult for mixing to occur, so microfluidic systems that rely upon mixing (from chemical synthesis to biological analysis) need another method. Passive mixing utilizes the geometry of the channels to mix the solution. This is built into the system, so it does not involve any external force. This can be easier to use than active mixing since once it has been made it can be left alone. However, different configurations of passive mixing lead to different extents of mixing done. Recirculating liquid plugs within droplets is an effective form of passive mixing that uses plug flow to get the desired level of mixing.[3]

Chaotic Advection
Chaotic advection is a model of fluid flow that works well for microfluidic systems[4],[5]. It assumes that the fluid is incompressible (which means constant material density at a given point along the channel) and laminar flow with no slip at the boundary. In laminar flow, what is typically seen is passive advection, in which the motion of particles in the fluid simply follow the flow of the bulk fluid. Chaotic advection uses this property and changes the flow within the drop using the geometry of the channel to mix the content of the drop while maintaining laminar flow.
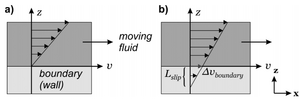
No-Slip Boundary Condition
The no-slip boundary condition assumes that velocity of the fluid directly in contact with the barrier (channel walls) is equal to the velocity of the barrier (in a stationary system, there is no fluid motion at the boundary)[6]. At micrometer scales using a water base this is often a valid assumption[1]. Hydrophobic surface exhibit potential slip at the nanometer scale, so the liquid in the channel can be approximated as a continuum with negligible slippage.
How it works
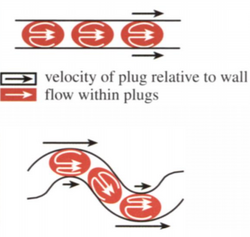
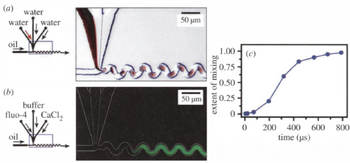
Recirculating liquid plugs in droplets works by having chaotic advection in droplets[2],[7]. First, droplets are formed by having multiple miscible inlet streams converging into one immiscible stream, forming a droplet with multiple aspects to be mixed. When the droplets form plugs in the channel (with the edges of the drops touching all of the sides) the flow within the droplet begins to circulate forming 3D advection. Due to the no-slip condition, the parts of the droplet in contact with the walls stay static while flow continues to move inside of the plug, pulling the plug along. If the walls are completely straight we get radially symmetric mixing along the channel, but if we change the channel geometry we get more advanced mixing. When the droplet travels along a curved surface, the symmetry is lost as the outside of the curve has more surface area in contact with the wall than the inside of the curve. As a result, there is a wider rotational flow on the side of the drop on the outside of the curve and a smaller rotation on the inside of the curve. After several twists like this in alternating directions the individual droplets can be considered to be fully mixed.
The time to mix a droplet using recirculating plugs is dependent on [math] w[/math], the channel width; [math] \sigma[/math], the Lyapunov exponent associated with stretching fluids, assumed to be 2 for simpler calculations; [math] n[/math], the number of fold, stretch, and reorient cycles; [math] D[/math], the diffusion coefficient for the components involved; [math] U[/math], the flow velocity; and [math] a[/math], the length of the plug in terms of widths of the channel.
We can look at the time until mixed based on the time it would take for each plug to mix by diffusive mixing, which is defined by:
[math] t_{diff} = w^2 * \frac{\sigma^{-2n}}{2D} [/math]
We can further say that [math] n[/math] is dependent on the Péclet number, [math] Pe[/math], which (assuming [math] Pe[/math] is large) approximately simplifies to:
[math] n = log(Pe) [/math]
[math] Pe [/math] is the ratio of advection to diffusion in a system, and for a microfluidic system is defined as:
[math] Pe = \frac{wU}{D}[/math]
Finally, a relationship between diffusive mixing and mixing through chaotic advection is formed:
[math] \frac{t_{diff}}{t_{mix}} = \frac{Pe}{a*log(Pe)} [/math]
This shows that total mixing by chaotic advection and recirculation is faster than typical diffusive mixing by a factor of Pe/log(Pe). Due to the speed of the plugs necessary for this system, this mixing is complete on the microsecond scale, as shown in Fig. 5.
Current Use
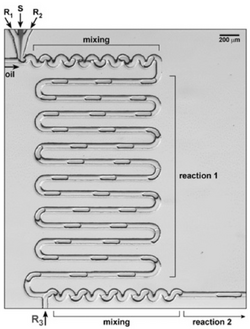
Recirculating liquid plugs within droplets requires easy to fabricate plastic chips to be done on as well as some kind of pressure source, so it is very accessible to a variety of fields[2]. It could be used for purposes such as separations, mixing, encapsulation, chemical and biological analysis, and much more[8]. Because of it’s effective mixing, any scenario in which chemical reactions are needed can use this method. With the growth of lab-on-a-chip technology, it is becoming increasingly possible to test for diseases and drug effectiveness and even grow organs, all of which depend on effective mixing so recirculation would be an effective approach. One example of a practical use would be to control assembly and shape in solution, such as 3D printing hydrogels in solution[9]. With multiple reagent feeds, it is possible to control the kinetics of the reaction by altering the shape of the device, and even to do multiple reactions with additional reagents added later on.
References
1 Che, Z., Wong, T. N., & Nguyen, N.-T. (2011). An analytical model for plug flow in microcapillaries with circular cross section. International Journal of Heat and Fluid Flow, 32(5), 1005–1013.
2 Song, H., Tice, J. D., & Ismagilov, R. F. (2003). A Microfluidic System for Controlling Reaction Networks in Time. Angewandte Chemie International Edition, 42(7), 768–772.
3 Ward, K., & Fan, Z. H. (2015). Mixing in microfluidic devices and enhancement methods. Journal of Micromechanics and Microengineering, 25(9), 94001.
4 Aref, H. (2002). The development of chaotic advection. Physics of Fluids, 14(4), 1315–1325.
5 Cartwright, J. H. E., Feingold, M., & Piro, O. (1999). An Introduction to Chaotic Advection. In Mixing (pp. 307–342).
6 Rapp, B. E. (2017). Fluids. In Microfluidics: Modelling, Mechanics and Mathematics (pp. 243–263).
7 Bringer, M. R., Gerdts, C. J., Song, H., Tice, J. D., & Ismagilov, R. F. (2004). Microfluidic systems for chemical kinetics that rely on chaotic mixing in droplets. Philosophical Transactions of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences, 362(1818), 1087–1104.
8 Dore, V., Tsaoulidis, D., & Angeli, P. (2012). Mixing patterns in water plugs during water/ionic liquid segmented flow in microchannels. Chemical Engineering Science, 80, 334–341.
9 Robertson, K. (2017). Using flow technologies to direct the synthesis and assembly of materials in solution. Chemistry Central Journal, 11(1).
