User:Nuri Purswani/Network/Discussion

Algorithms for Biological Network Reconstruction from data

Home

Introduction

Synthetic Datasets

Methods

Results

Discussion

References

Results

Overview

Having done preliminary simulations on three in silico examples (Ring, Chain and Double Ring) we are now in a partial position to discuss the relative capabilities of both method. Why partial? In order to fully validate the conclusions we require more datasets for the comparison, including examples of more realistic biological networks. This work is in progress, and we expect to obtain more conclusions in the next few weeks. The main points covered in this discussion are:

• General Comments on the results, with respect to:
  • Varying signal-to noise ratio
  • Varying number of experimental repeats
  • Varying input perturbation
• Steady state vs time series measurements
• Is it good to be overambitious?
• Which Method do I recommend? Relative Capabilities and Limitations from the point of view of the user
• Future Work
  • The Possibility of a new "debugging tool" for synthetic biology
• Conclusion

General Comments on the Results

The Robust control method performed substantially better obtaining scores of perfect sensitivity and specificity for the ring example and performed better at inferring substructures in the double ring example than the bayesian inference method. The chain example was problematic, partly because it was realised that the dc offset was a necessary step, so this system would in practice have zeros in the G matrix, making the problem unsolvable by the robust control method (see explanation in later subsection). Therefore our preliminary simulation results show the following summaries of performance:

Performance varying signal-to-noise ratio

The robust control method outperformed the bayesian inference method, by recovering correct sub-networks in the chainexample at a higher sensitivity and specificity than the bayesian inference method.

Chain

For the highest signal to noise ratio in the chain (57000):

• Case 1:The robust control method recovered the correct network structure at sensitivity = 1 and specificity = 1. While the bayesian inference method also found the network at sensitivity=1, its specificity was = 0.33 which is low, as it means that it found all the false positives and gave a result that was close to the nearly connected network. For lower (worst) signal to noise ratios, the sensitivity dropped gradually in the bayesian inference method, while in the robust control it had a cutoff at SNR=1888 (this is an approximate figure, and I may have used a different convention to calculate SNR).
• Case 2: The robust control method and the bayesian inference method were both unable to recover this substructure at sensitivity and specificity=1. The 5th AICc score recovered it at sensitivity=0.75 in the robust control method, but this may not be a good indication as it may have arisen by chance. This is a subtle difference between the two approaches. While the bayesian inference method uses confidence intervals, the robust control approach can be seen as "binary"- (i.e. it either finds the network or it doesn't). Sometimes it can identify "candidate structures" for the true topology which are ranked using the AICc. This points to a future investigation of possible scoring schemes.

Double Ring

For this range of signal to noise ratios, none of the algorithms 'broke down'. The robust control method recovered the substructure in this experiment at perfect sensitivity and specificity. The bayesian inference method recovered it at sensitivity=0.75 and specificity=1 for the z=3 significance threshold. Overall, the robust control method performed better on this example.

Sensitivity and Specificity

An important point to note is that we chose to use these two quantities as measures of algorithmic performance, because they are widely used in the systems biology community. ROC curves do not apply here, as there are no confidence intervals to vary in the robust control method. For ROC curves assessing Beal's method individually see Beal et al 2007. In this cited example, they tested their algorithm on a network by Zak et al. (Zak et al. 2003) and obtained an accuracy of 70% area under the ROC curve, which got better by adding prior knowledge about the network. This network contained 54 nodes, so the quantities of sensitivity and specificity were a suitable indication of the algorithm's performance.

In these examples, the size of the datasets (from 3 to 8 nodes) was significantly smaller, so the ratios of senstivitiy and specificity that we found should not be taken as stand alone. In order to truly assess their performance we require more datasets, including biological examples.

Performance varying number of repeats of the experiments

This test utilized the ring network as input, and here we assessed the ability of both methods to recover the true network structures at 100% sensitivity and specificity, by varying the signal to noise ratio (a.k.a the experimental noise variance) and the number of repeats. The robust control method outperformed the bayesian inference method, as it was able to recover the correct network structure at 100% sensitivity and specificity, while the bayesian inference method only recovered it at 1% sensitivity and 0.67% specificity (it had 1 false positive) for all the repeats and noise variances implemented. These simulations should be repeated. For the time being, we can state that in this particular example, the robust control method can recover the true network with less experimental repeats and can also tolerate more experimental noise at any given trial.
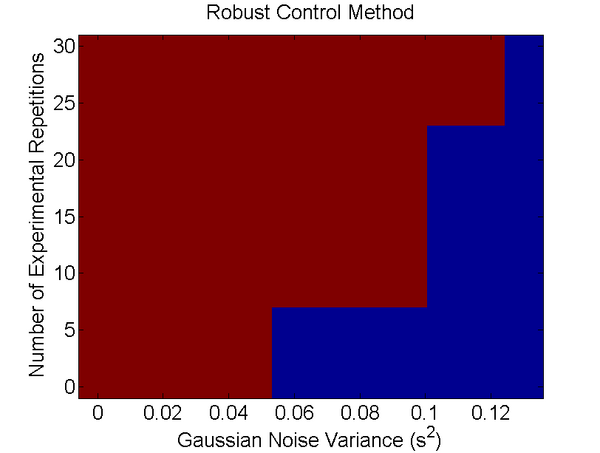
Figure 1:Ability to perfectly recover boolean structure of the ring network for different numbers of repeats (N=3,9,18,27) and noise variances. In this example red= The correct structure was found as the best AICc score and blue= The correct structure was no longer found.

Due to limited amounts of time, this test was not validated in other examples, so more work is needed to verify this conclusion.

Varying the type of input perturbation

Reminder: By variation of input disturbance we mean the following:

1. Step Disturbance: Stimulate each measured node in turn (on a different experiment) with a step input
2. Gaussian Disturbance: Stimulate all three measured nodes at the same time for N experiments of Mean 1 and varying standard deviations

An illustration is shown below:

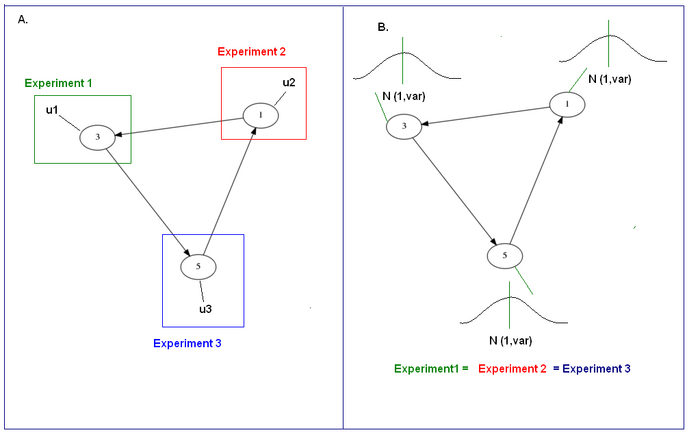
Figure2 : A. Step perturbation on every measured node. B. Noise perturbation on all measured nodes at the same time.

Step Perturbation

• Recovered the true network structure at 100% sensitivity and specificity in the robust control method.
• Recovered the network structure with false positives in the bayesian inference method (see results for previous section)

Gaussian Noise Perturbation

Here we were unable to recover the correct network structure in all the implementations attempted for both the bayesian inference and the robust control methods.

Possible theoretical explanation

There is a hypothesis regarding this perturbation that we would like to investigate further. The bayesian inference method requires a time-series, as it relies on the intrinsic noise of the system to recover biological network structure. The noise perturbs the dynamics of the system. Beal et al. and Rangel et al. claim that they can recover topologies using these methods, without external perturbations.
This cannot work with steady state data, as the algorithm needs the transient response of the system to infer dynamical structure.

A puzzling finding when contacting Prof D. Wild (one of the co-authors of both methods above) was that the reference they provided to an in silico implementation by Zak et al. (2003) already contained an input perturbation. In this paper, they asessed the importance of a step perturbation and input pulses on identifying the parameters in their in silico model. They concluded that the step perturbation was better at identifiying transcriptional interactions when the number of cells is small, while the pulse was better at larger cell numbers. Naturally, their findings relate to the specific properties of their model.

The step perturbation is a point that requires further detailed examination. We attempted to contact the authors about this result, but did not get very clear responses on a first instance. More work is needed, but we believe that the input disturbance is a necessary step for network reconstruction, as outlined in Gonçalves et al. 2008.

Ability to recover substructures in a complex network

We saw in the last example with the double ring that the robust control method was on average, better at identifying substructures within the complicated network. However, none of them yielded perfect results at 100% sensitivity and specificity for all topologies. Particulary troublesome motifs are shown below:

1. The robust control method guessed this topology in the 2nd best AICc value at 100%, while the bayesian inference method had false positives and negatives

1. The robust control method guessed this topology in the third best AICc value at 100% sensitivity, while the bayesian inference method had false positives and negatives. Generally the z=3 confidence level has a slightly lower sensitivity, but is not as prone to false positives.
   

Troublesome feedback loops

A possible explanation for the troublesome findings can be linked to the presence of feedback loops in the network. The chain example proved to be very problematic for inference (although the simulations need to be re-done) but it may be possible that the presence of feedback loops may sometimes "blurr" specific interactions. It is important to be able to cope with these accurately, as loops are ubiquitous in real biological networks. More validation is needed on biologically relevant networks to continue expanding the comparison. To achieve this we first need to increase the computational power of the robust control algorithm, so that we can sample more measured nodes and test it in networks with biological relevance.

Steady State vs Time Series Measurements

As mentioned earlier on, there was a clear difference in the inputs that both methods take. In this comparison we assessed the ability of both methods to recover the boolean structure of a network of interest. By this term, we refer to the following:

• Robust Control Method:
  • Entries in matrix Q(0): The Control Structure Function - See Gonçalves and Warnick 2008 for an explanation and also Methods .
• Bayesian Inference Method:
  • Significant entries in the matrix CB+D of interactions (See Methods and Rangel et al. 2004).

In order to do this comparison, the Robust Control method took steady state measurements, while the Bayesian method required a time series, and generally would not cope well with gene expression levels close to steady state (results not shown due to lack of time to write up, but available on request). Despite having fed the Bayesian inference algorithm multiple timepoints (ranging from T=20 to 700), this method was still unable to recover the boolean structures of all three networks at a perfect sensitivity and specificity.

In reality, we will not be able to obtain more than 20-30 time points per experiment (Wu et al. 2006) which altogether makes the inference task harder. Even if we were able to sample more often, we will never be capable of obtaining every detail of the dynamics of the system. Furthermore, there is no guarantee that we will capture the dynamics of the transient phase of gene expression, as this would require being able to sample at the start of the reaction, which is physically impossible. In practice, the steady state is much easier to obtain, and in these simulations, the robust control method with steady state inputs has been able to outperform this Bayesian method with time series inputs.

Is it good to be overambitious?

As outlined in Gonçalves et al. 2008, many network reconstruction methods tend to choose particular realizations of network structure given a transfer function, and then justify their objective function of choice assuming, for example that the "best structure" is the sparsest realization. The Robust control method assumes this to a certain extent, as the Akaike Information Criterion (AIC) penalizes too many connections.
In Gonçalves et al. 2008 it is shown that without any extra information about a biological system, any network topology is possible given an input and output. This puts the usefulness of several in silico methods into question*.

While Rangel et al. , Beal et al. and Alche-Buc et al. 2007 aim to infer the full state space representation of the network, the Robust Control approach focuses on "explaining only what we see". This involves inferring the structure of indirect reactions between measured species, and opting for a more modest approximation of the system, instead of an estimation of the full state, where there is no certainty about the hidden state parameters.

The CB+D matrix of interactions can be seen as the analogous equivalent of the dynamical structure function from the robust control method. However, the ability to recover network structure relies on confidence thresholds (z statistic), which have to be constantly adjusted to find the best score. The robust control method's analogous ranking is the AICc although future work should explore alternative information criteria which could also perform well at identifying highest scoring networks.

(*) so option A. Develop a new method or B. take up a career in divination.

Relative Capabilities and Limitations

Both methods have relative capabilities and limitations, which we list and explain in the two sections below. Then we provide a recommendation to the user about what method is the "best pick".

Robust Control

Capabilities

• Robustness: The method is very powerful and has been able to predict boolean structures, with the exception of the chain. This is due to the robustness of the step perturbation. Systems relying on the intrinsic noise of the system may at times be successful in recovering network structure, but this does not guarantee that the dynamics will be sufficiently perturbed. Furthermore, in order to be able to infer network structure without any external inputs, the system's transient response must be measured, and due to experimental limitations, mentioned in steady state vs time series measurements, it is not always possible. From our preliminary simulation results we saw that relying on the intrinsic noise of the network did not recover the correct structures, while perturbing the systems with a step did have a higher success rate. Furthermore, the steady state is much easier to obtain, and overall, this method does not require so many repeats to infer network structure, which is not the case for the bayesian inference case.
• It can cope with non linearities not too far from an equilibrium point

Limitations

• Lack of experimental data to validate this method: For this comparison we have not been able to use real datasets, as the robust control method requires that we perform experiments (such as gene silencing or overexpression) to perturb each observed experimental quantity in turn. This reduces the current credibility of the results, although work is in progress. Due to its input requirements, it may not be able to cope with most of the datasets in the DREAM competition, but this needs to be explored further.
• G(0): This algorithm cannot cope with zeros in the transfer function. During the implementations, several networks could not run on this algorithm, as it requires that all observations are perturbed in every experiment, which was the case with the ring and the double ring networks. The reason for this is that when a steady state measurement goes close to zero, the signal to noise ratio becomes too large for the algorithm to cope with. This also means that every experiment must perturb every observed quantity, else when we subtract the dc value (as part of the data normalization procedure), an unperturbed signal will have the exact same value as it had at steady state and as a consequence set itself to zero. Further checks on the chain example showed that this was the case, which is one of the reasons why the algorithm was unable to perfectly recover its boolean structure.
• At present, the size of the datasets that we have tested this method on are in a much smaller scale to what we will obtain in "real biological data". We have only output results for up to three measured nodes, as there are certain computational limitations in computing possible structures that are higher than this. This is because for a number [math]\displaystyle{ p }[/math] of measured nodes, there are [math]\displaystyle{ p^2-p }[/math] possible boolean structures. This makes it an combinatorially hard problem to solve. For 8 nodes, at present it will take 300 years to obtain the correct boolean structure. The bayesian methods have tested their algorithms on datasets of sizes up to 88 nodes (Rangel et al. 2004). This means that the comparison needs to be expanded on examples that are more directly comparable to what they have already implemented. A good example to implement will be a gene regulatory network published by Zak et al. 2003, where they also discuss the importance of the input perturbation.
• Linear time invariance assumptions: Although this method can cope with noise and non linearities (provided they are not too far from equilibrium), it breaks down in truly non-linear systems such as the repressilator (Ellowitz 2000). Alche-Buc et al. 2007 published a method that uses [ http://en.wikipedia.org/wiki/Kalman_filter#Unscented_Kalman_filter unscented kalman filtering] to recover non linear interactions, although it still requires prior knowledge of the boolean network structure before performing the inference task.

Bayesian Inference

Capabilities

• It's "realistic": Rangel et al. and Beal et al.'s methods are well established in the systems biology community, and they have been tested on both in silico datasets and microarray experiments. This automatically gives them more credibility. In their previously published results (Beal et al. 2007,2010) they mention that they can obtain a 70% area under the ROC curve for inferring network structures, which increases with prior information about the network. As part of the training for the optimization algorithm, they provide the option of entering a "partially known" network structure. This means that if the user has some idea of what the network may "look like", they can then proceed and provide a refinement.
• Ability to cope with non linearities:They published in Beal et al. 2007 their results for network inference in a model by Zak et al. (2003), which contained non linear relationships such as: mutual repression, autoactivation, sequrestration, agonis induced receptor down regulation...

Limitations

• It requires a time series and several experimental repeats to provide accurate results: This method cannot infer networks with a single steady state measurement and requires several repeats to be able to infer the networks at 70% area under the ROC curve (see reference above).
• Low sensitivity and specificity: Although published results (Rangel et al. 2004, 2005, Beal et al. 2005, 2008, 2010) show that the algorithm's sensitivity and specificity increase with more repeats and time points, we have not been able to show this in the datasets we used. In our results it seems that these methods perform better in high signal to noise ratios, but the robust control method is better at coping with noisy data. This is contrary to our original beliefs, as this method did require noise as a disturbance. Further simulations are required to validate this point.

Recommendations for the user

So, if I were the user... which method would I recommend?: The robust control method has not been tested on 'real' datasets, so for experimental measurements that have not been done according to the guidelines earlier, (i.e. The number of experiments must equal be equal to the number of observed quantities and every species must be perturbed individually on each experiment ) the method will not work.
Beal et al.'s method has been tested on experimental datasets and in silico biological networks with 'realistic' properties. The robust control method has been tested on the chemotactic pathway of the rodhobacter spheroides (Porter et al. 2004) and can be applied to real datasets, although prior knowledge of the system is required. So my recommendations are the following:

• If you have time-series data from a microarray experiment, multiple repeats and prior knowledge about parts of the network you are trying to infer, Beal's method is a good bet, as it has previously been shown to recover network structures with some limitations on relative sensitivity and specificity.
• If you have steady state measurements but have not perturbed each quantity individually, none of these methods will be able to recover network structure. So provided you have an acceptable signal to noise ratio, it would be worthwhile to proceed as per the recommendations in the Future Work section.

Future Work

• Explore more methods mentioned in the literature review. More thoughts about the relative capabilities of the methods are provided in that section, so it can be considered a "part-discussion" review.
• Try different information criteria and scoring schemes as they may be able to provide better results than AIC, BIC AICc and the eucledian distance measure for the robust control method.
• Investigate further the effects of input perturbations on capabilities of both methods to recover network structure. Zak et al 2003 is a good starting point, as it's the in silico implementation that worked previously in Beal 2005.
• Increase the number of test datasets, including variations in their sizes and also test more examples that have previously been validated in the Beal et al. method.
• Test on more biologically relevant examples. The rhodobacter is underway, and also Zak et al. 2003
• ...or redesign biological experiments-

A debugging tool for synthetic biology?

Synthetic biology uses modeling and design to construct these artificially. Groups that have taken this “synthetic biology” approach include Hasty’s recent implementation of a synchronized population-level oscillator (Hasty et al. 2010), Weiss et al’s implementation of e-coli bandpass filters (Weiss et al. 2007) and more recently, Cantone et al. , who utilized an artificially synthesized gene network in yeast for the assessment of the performance of various algorithms in inferring correct network topologies.

Being able to “reverse engineer” biological systems and implement these ideas on artificially constructed, well characterized examples offers a promising next step in the understanding of gene regulatory processes, which can be scaled up to comprehending more complex networks. The natural next step forward to this approach is to validate it experimentally, by constructing a synthetic network and assessing its performance at inferring the "underlying design".

At present there is a great desire in the synthetic biology community to develop CAD tools for design of biological devices. The algorithm from Goçalves et al. can be seen as the analogous of the "voltmeter and ammeter" in an electric circuit. It has the potential to develop into a robust approach to inferring biological networks, and also a powerful tool for bio-inspired design.

Conclusion

More work is needed to truly asess the relative performance of both methods. Preliminary simulation results from in silico experiments suggest that the robust control method with steady state measurements is able to recover boolean network structure at a higher sensitivity and specificity than the bayesian inference method with a time series. In addition, we were unable to recover network interactions in the absence of a step disturbance at each individual node, which suggests that an input at every node is necessary to be able to reliably infer network structure. With Gaussian noise, both methods were unable to recover the network topologies. Therefore, summarising performance, these were our main findings:

• The robust control method has a higher sensitivity and specificity at low signal to noise ratios on the datasets we implemented.
• The robust control method has a higher sensitivity and specificity and a higher noise tolerance and with less experimental repeats than the bayesian method.
• Both methods are able to cope with non-linearities.
• The robust control method outperformed the bayesian inference method at recovering 'sub structures' in networks of complex topologies.
• Neither of the methods were able to recover network topology with gaussian noise input perturbations. When the perturbation was a step input, the robust control method recovered network structure at a higher sensitivity and specificity than the bayesian inference method.
  

Recommendations for the user: At present, the robust control method needs further validation, so it cannot be used directly on real datasets, since it requires experiments to be performed in a specific way. Provided that these experimental criteria have been met, if the user has steady state measurements, then the robust control method is a better option than the bayesian inference method. For time series measurements both methods are useful in practice but we still require further simulations for an accurate validation of the algorithms to strengthen our conclusions.