User:Geoff S. Baldwin/Sandbox
My Sandbox
Section 1
Sub-Section
- bullet point
- bullet point
- bullet point
- bullet point
Section 2
- topic 1
- topic 2
- topic 3
<html> <body> <script type="text/javascript"> var sc_project=3315875; var sc_invisible=0; var sc_partition=36; var sc_security="779debd0"; </script>
<script type="text/javascript" src="http://www.statcounter.com/counter/counter_xhtml.js"></script><noscript>
</noscript>
</body> </html>
Practical 1
Objectives:
- To learn how to use a computational modelling tool for biochemical reaction simulations.
- To build biochemical networks
- To simulate the time evolution of the reactions
- To explore the properties of simple biochemical reactions.
- A --> B --> C model
- Synthesis-Degradation model
- Michaelis-Menten model
Deliverables
- A brief report is expected ( see structure). Report due Monday 18th February 2008.
- When you find in the text (illustration needed), it means that you will have to provide an image export of your simulation results in your report.
- Instructors: Vincent Rouilly, Geoff Baldwin.
Part I: Introduction to Computer Modelling
- "All models are wrong, but some of them are useful", George Box.
Part II: Getting to know CellDesigner
- Read through the tutorial example, and get familiar with CellDesigner features. Official CellDesigner Tutorial
- Open a sample file: File -> Open -> Samples/...
- Select items, move them around, delete, undo...
Part III: Building Your First Model: A --> B --> C
In this section, you will build your first model from scratch with CellDesigner, and you will learn to run a simulation.
The model explored describe a system where a compound 'A' is transformed into a compound 'B', which is consequently transformed into a compound 'C'.
To start, launch the CellDesigner Application: Double Click on the Icon found on your Desktop. Then follow the instructions below to build the model.
| Model | CellDesigner Instructions |
|---|---|
|
Following the Law of Mass action, the dynamic of the system is described as: |
|
| Simulate the dynamical behaviour |
|
- Questions:(see report structure)
- How do A, B and C, change with time using these default parameters?
- Now swap the values of k1 and k2 (k1=10 and k2=1)under the parameters tab
- How does this alter the formation of C?
- How does B change?
- Explain these results
- If you had real life data showing the accumulation of C for an A-B-C reaction you could fit the data using this model and two rate constants would be returned. Could you assign these rate constants to k1 or k2 (yes or no)?
- What additional data would you need to assign k1 and k2?
- Additional Resources:
Part IV: Synthesis-Degradation Model
In this section, we investigate a very common motif in biochemistry. It models the continuous and constant synthesis of a compound, and its natural degradation.
From a Mathematical point of view, the model is described as a first-order linear ordinary differential equation.
| Model | CellDesigner Instructions |
|---|---|
Build the topology of the reaction network
| |
From the law of mass action, we can write:
|
Define the kinetics driving the reaction network
|
| Simulate the dynamical behaviour |
|
- Questions:(see report structure)
- Run a simulation over t=1000s, nb points=1000. Comment on the time evolution of 'A'. (illustration needed).
- Using the dynamical system definition, what is the steady state level of 'A' with regards to the parameters k1 and k2 ? (Steady state means that [math]\displaystyle{ \frac{d[A]}{dt}=0 }[/math]
- Using the 'Parameter Scan' feature, illustrate the influence of both parameters (k_1 and k_2), on the steady state level of 'A' (illustration needed).
- Bonus: Give the analytical solution of the ODE system.
- Now, consider that k_1=0, and [math]\displaystyle{ [A]_{t=0}=A_{0} \gt 0 }[/math]. Keep k_2=0.01. Illustrate the concept of half-life for the compound 'A'.
- Bonus: Derive the analytical expression of the half-life of 'A', with regards to k_1 and k_2.
- Additional Resources:
Part V: Michaelis-Menten Model
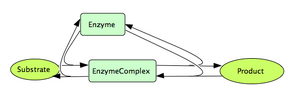
An enzyme converts a substrate into a product, this is usually an irreversible reaction and is treated as such in the Michaelis-Menten model. An enzyme reaction constitutes a dynamic process and can be studied as such. One may look at the time courses of the reactants, or look at the steady-states and their stability properties.
This part of the tutorial deals with well-known Michaelis-Menten formula.
Here, we will focus on comparing the Michaelis-Menten approximation to the full enzymatic reaction network.
| Model | CellDesigner Instructions |
|---|---|
| |
| Following law of mass action, we can write:
[math]\displaystyle{ \begin{alignat}{2} \frac{d[E]}{dt} & = k_{2}[ES] - k_{1}[E][S] + k_{3}[ES] \\ \frac{d[S]}{dt} & = k_{2}[ES] - k_{1}[E][S] \\ \frac{d[ES]}{dt} & = k_{1}[E][S] - k_{2}[ES] - k_{3}[ES] \\ \frac{d[P]}{dt} & = k_{3}[ES] \end{alignat} }[/math] |
Questions:(see report structure)
- From the ODE system description, create all the necessary kinetics reactions in the network provided. We will be considering [math]\displaystyle{ K_{1}=10^5 M^{-1} s^{-1} }[/math],[math]\displaystyle{ K_{2}= 1000 s^{-1} }[/math],[math]\displaystyle{ K_{3}= 10^{-1} }[/math],[math]\displaystyle{ K_{4}= 2 M^{-1} s^{-1} }[/math],[math]\displaystyle{ [E]_{t=0}= 0.01 M }[/math],[math]\displaystyle{ [S]_{t=0}=0.01M }[/math],[math]\displaystyle{ [P]_{t=0}=0 }[/math]
- Open the Simulation Panel, set Time=150, NbPoints=1000.
- Run a simulation, and comment on the different phases during the product formation. Pay special attention to the formation and decay of the [ES] complex. Note that this is a full simulation of the reaction scheme and so does not rely on any assumptions.
| Model | CellDesigner Instructions |
|---|---|
|
|
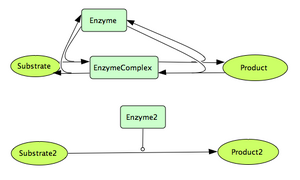
- We want now to investigate the Michaelis-Menten approximation. Show that under the assumption that the complex [ES] is at steady-state ([math]\displaystyle{ \frac{d[ES]}{dt}=0 }[/math]), we can write: [math]\displaystyle{ \frac{d[P]}{dt}= \frac{Vmax[S]}{Km+[S]} }[/math]. (Note that [math]\displaystyle{ [E]_{t=0}=[E]_{t}+[ES]_{t} }[/math]). Also, make sure that the concentration of the substrate is at least 10 fold greater than the concentration of the enzyme.
- Express (Km and Vmax) with regards to K_1, K_2, K_3 and [math]\displaystyle{ [E]_{0} }[/math]; see the links below on how the Michaelis-Menten equation is derived if you are not sure.
- Now create a new reaction in CellDesigner(as shown above)with an Enzyme that acts on the reaction. Define the maths for this reaction based on the above form of the Michaelis Menten equation. Make sure that both models are equivalent with regards to their parameters.
- Run simulations, and comment on the differences observed between the full model, and the Michaelis-Menten approximation.