Todd:Chem3x11 ToddL13
Chem3x11 Lecture 13
This last lecture is about two other classes of pericyclic reactions, namely cycloadditions and sigmatropic rearrangements.
(Back to the main teaching page)
Key concepts
- Cycloadditions and sigmatropic rearrangements are governed by similar orbital considerations to those we've already seen
Cycloadditions
Cycloadditions are pericyclic reactions where two components come together to give a cyclic compounds. The best-known example is the Diels-Alder reaction. The reaction occurs between a diene (with 4 π electrons) and a dienophile (with 2 π electrons); we talk of this reaction being a [4 + 2] cycloaddition. Three π bonds and a σ bond in the starting materials become one π bond and five σ bonds in the product.
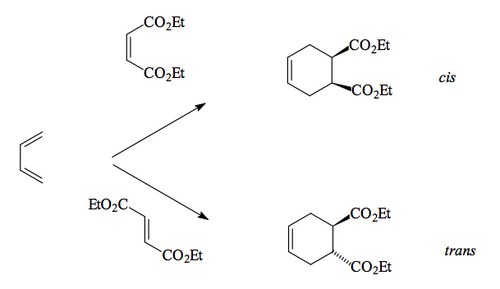
Again, there are no intermediates, just a cyclic transition state. The stereochemistry of the starting materials is carried through to the products, as can be seen by the above example. We need to explain why this is, as well as explaining other things about the reaction.
General Orbital Requirements for a Diels-Alder Reaction
As for electrocyclic processes, the lobes of the MOs on the interacting atoms need to be in phase. We should look at the frontier orbitals of the two reagents. Looking at the diene and dienophile drawn on paper, it's not clear which interaction is most energetically likely, but it turns out the HOMO of the diene interacts with the LUMO of the dienophile. (The other interaction is symmetry-allowed, but the orbitals are often quite far apart in energy and do not dominate the interaction unless the electronics of the reagents are unusual, giving what are called "inverse electron demand Diels-Alder reactions" which we don't cover.)
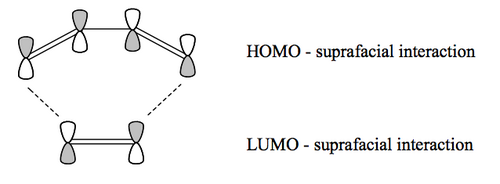
You'll notice that the two components approach and interact using MO lobes that are on the same face of each. i.e. the diene uses two lobes on one face and the dienophile uses two lobes on one face. This is a suprafacial-suprafacial interaction. The interaction between diene and dienophile is very sensitive to what's attached to the different systems. The simplest DA reaction on paper is very hard to get to go, but small steric and electronic changes to the structures of the reagents means the reaction can go very quickly.

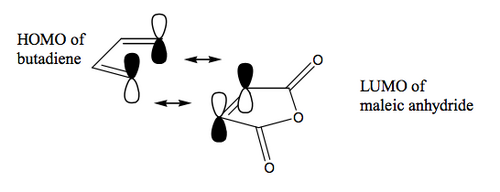
The activation of the dienophile in the case above is electronic in origin. If we are to promote a cycloaddition, we need the frontier orbitals (of the right symmetry) to be close in energy - that provide the greatest energetic benefit when the new bonds are formed.
Usually a DA reaction employs an electron-rich diene. If it's electron-rich, it has a high energy HOMO. It thus helps if we have a low energy LUMO to go along with this HOMO, and we can achieve that by making the dienophile electron poor. The simplest way to do that is attach a group that is electron-withdrawing to the π system, for example a conjugated carbonyl group. Obviously the interacting orbitals are the ones shown here, and this diagram should bring some questions to your mind about the three-dimensional nature of this interaction, which is the cool thing we'll get to in a moment.
The other (more obvious) way to accelerate a cycloaddition is to arrange the diene in an orientation that promotes the reaction. This is why you typically see fast DA reaction employ cyclic compounds like cyclopentadiene.
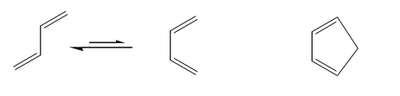
The Stereochemistry of the Diels-Alder Reaction
There are two ways the diene and dienophile can approach each other - either "end-to-end" where there is the minimum of steric interaction between reagents, and the minimum of steric crowding in the product, or "folded over" where the two components approach sandwich-style.
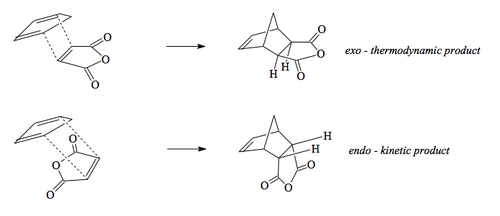
When you perform a DA reaction and tune the conditions so that the reaction just goes (i.e. a high enough temperature to see conversion) you find the product you get is the "folded-over" product which we call the endo isomer. This is the kinetic product. Given that all cycloadditions are reversible, we can heat the reaction more to see if we get another product, and sure enough we do. The thermodymanic product is actually the other isomer, the exo isomer. The question is, what controls this?
If we draw out the interacting MOs in full, rather than just the end lobes of the p system, we see an extra feature. In the diagram below, note that the MO for the dienophile now includes the two carbonyl groups attached. When we include those in our MO diagram, and construct the LUMO, we find that some of the orbitals present interact with the right symmetry. These secondary orbital interactions do not give rise to new bonds, but are stabilising of the transition state and accelerate the reaction to the endo isomer. Ultimately, though, the steric congestion in the endo isomer is unfavourable compared to the less sterically congested exo isomer and the thermodynamic product will be obtained, if we push the reaction hard.

Brief Note on Photochemical Cycloaddition Reactions
We don't cover these in much detail here, but the arguments are similar to the ones we saw with electrocyclic reactions. The selectivity changes between thermal cycloadditions (those we've been looking at so far) and photochemical ones. To see why, let's look at a cycloaddition reaction that looks reasonable on paper, but doesn't actually proceed - the reaction of ethene with itself to give cyclobutane. The problem is one of orbital symmetry and geometrical constraint. The required HOMO and LUMO interaction can't happen because one of the alkenes can't "reach round" the side of the other. More formally, the interaction needs to the antarafacial, but a suprafacial interaction is imposed by geometry.
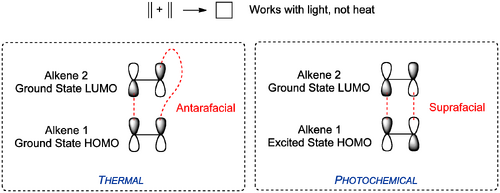
Here's an example of a real case:

Overall, for cycloadditions, we can again formulate some rules of thumb about what is allowed. For example if the combined total number of π bonds involved in the reaction is odd, and we're trying a thermal reaction (this describes the DA reactions we saw above) then the interaction has to be suprafacial. An even number of π bonds requires an antarafacial approach. Photochemical reactions reverse these rules. But, as before, you really need to be able to work out which orbitals are interacting in any given case, since that immediately dictates the way the reaction happens.
Sigmatropic Rearrangements
Some examples of sigmatropic rearrangements are shown below.
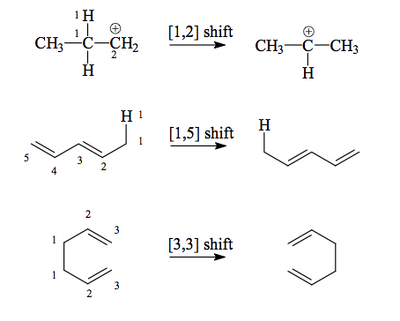
These reactions involve the concerted move of a σ bond across a π system. Unlike in the previous reactions we've seen, in these examples we can see migration of groups around a molecule. The terminology "[x,y]" indicates the position the original σ bond (the ends of which are labelled 1 and 1, which sets the numbering for the molecule) migrates to. We've met these terms already, but suprafacial and antarafacial are also used for these reactions to describe whether the migrating group moves across the same face of the π system or moves from one face to the other. As before, which reaction pathway occurs depends entirely on the symmetry of the relevant orbitals.
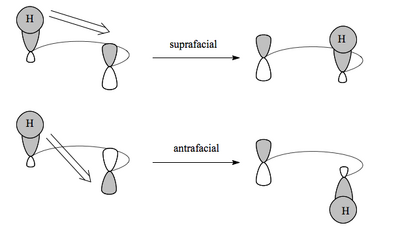
We'll look at a few different examples, because though the basic reasoning is always the same (symmetry of orbitals and the possibility of overlap) the orbitals involved vary depending on the system.
The [1,2]-Shift
This is very simple - the HOMO of the migrating group overlaps with the LUMO of a carbocation, and we see suprafacial migration.

The reaction is thermally allowed. The driving force is frequently formation of a more stable carbocation. The migrating group doesn't have to be a hydrogen atom.

The [1,3]-Shift
The shift of an H atom from an allylic position to the end of a double bond, with simultaneous movement of the double bond looks feasible. A consideration of the orbitals shows why it doesn't happen. In the ground state of the molecule we can take the HOMO of the sigma bond and the LUMO of the pi bond. We consider them to be in phase. A migration of the H would require an antarafacial migration, which is geometrically impossible.
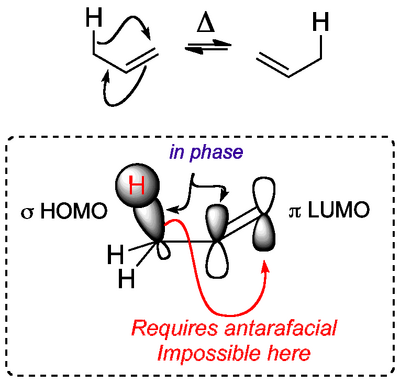
It turns out that the photochemical version of this reaction does proceed, but the mechanism starts to include significant radical character, and it's not straightforward, so we'll skip it here.
The [1,5]-Shift
A fairly simple motif in organic chemistry, a C-H bond off the end of a (Z,Z)-diene, can undergo a [1,5]-sigmatropic shift. The σ bond HOMO is in phase with the end lobe of its adjacent π LUMO, and when you work through the orbitals you find the phases match for a shift of the H to the 5 position.
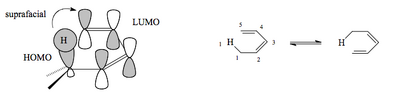
This is quite a simple shift to achieve, and partly explains the very facile rearrangements seen with cyclopentadienes.

The [1,7]-Shift
We could keep doing this all day, but looking at the [1,7]-shift is instructive since we see that there is an antarafacial requirement of the process.

Two Common [3,3]-Sigmatropic Rearrangements
Two widely-used sigmatropic rearrangements in synthetic chemistry are the Cope and Claisen Rearrangements. They are both [3,3].

The way to think about the frontier orbitals here is a little like a Diels-Alder reaction - a 4-electron HOMO component and a 2-electron LUMO component. The HOMO contains one of the π bonds and the migrating σ bond, but as a HOMO has one node.
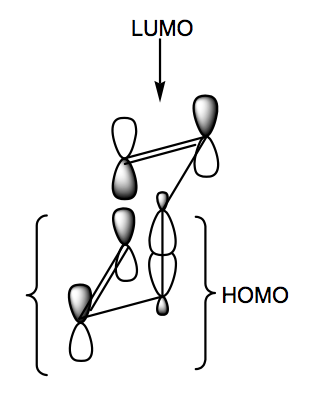
The ends of the interacting π bonds then have the right symmetry for a bond forming event. The transition state is chair-like, hence low in energy. Actually this reaction can go via a boat transition state, but it's not preferred. For further (non-examinable) reading, check out the Ireland-Claisen Rearrangement, which is used a lot in organic synthesis.
So overall the rule for sigmatropic rearrangements is that if an odd number of electron pairs is involved (either s or p), and it's a thermal reaction, we get a suprafacial process. Antarafacial if an even number of electrons. Swap all this for photochemical. But don't learn rules - work it out.
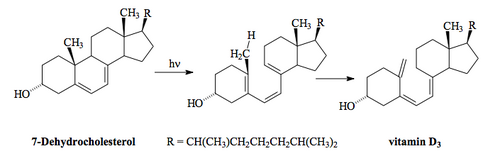
A Cool Example from Nature
Vitamin D is produced under the skin by a photochemical electrocyclic ring opening followed by a [1,7]-sigmatropic rearrangement.
An Overall Rule you can Learn if you Really Want To
The Electrons Circle Around. TECA. Can also stand for Thermal reactions with an Even number of Electron pairs are Conrotatory or Antarafacial. See?
The Licence for This Page
Is CC-BY-3.0 meaning you can use whatever you want, provided you cite me.
