Jennymchua Week 2 Assignment

Purpose

The purpose of Aipotu: Evolution was to determine if a certain population of red and white Aipotuian flowers was in Hardy-Weinberg equilibrium, and thus not evolving, based off of certain relative fitnesses for each of the two color types.

Methods/Results

Methods

Part A: Select for Red

For setting up the simulation, I disabled the Mutations feature to isolate a population of only red and/or white flowers.

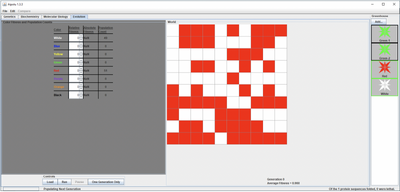
I clicked and selected on the red and white flowers in the Greenhouse in order to load the World screen with a nearly 50/50 distribution of red (49) and white (51) flowers.

Next, I set the relative fitness of the red flower to 10 (the maximum) and all the other colors to 0 (the minimum).
To run one generation of reproduction, I clicked the "One Generation Only" button so that the starting flowers could contribute to the gene pool based off of their fitnesses. At this point, the starting flowers began to die off to allow for 100 new offspring. Each offspring received two random alleles chosen from the gene pool.
I clicked the "One Generation Only" button until the population was completely red, which took eight generations.

Part B: Select for White

Both red and white flowers were once again selected from the Greenhouse to load the World with a nearly 50/50 distribution of red (48) and white (52) flowers.
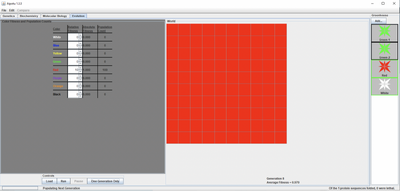
Rather than setting the relative fitness of the red flower to 10, the relative fitness of the white flower was set to 10 and all the other colors to 0.
I clicked the "One Generation Only" button until the population was completely white, which took two generations.

Part C: Hardy-Weinberg Equilibrium & Natural Selection

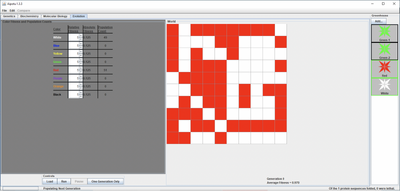
I loaded the world with only the Red flowers from the Greenhouse so that there were only Red flowers present.
In order to show the colors of both alleles in each flower, I checked the "Show colors of both alleles" button.
- A homozygous (RR) flower was a completely filled red square, while a heterozygous (Rr) flower was a red square with little white triangles in the upper left corner of each flower.
All fitnesses were then set to 5.
I calculated the expected allele frequencies in the starting population and the expected genotype frequencies at Hardy-Weinberg equilibrium.
After running the simulation for one generation, I calculated the observed genotype frequencies and compared them with the expected genotype frequencies at Hardy-Weinberg equilibrium. In order to see if this difference was significant, I used a Chi-Square statistical test.
I then set the fitness of red to 10 and all the other colors to 0.
I ran the simulation for a few generations then calculated allele frequencies.

Results

Part A: Select for Red

After setting the fitness of red to the maximum and all the other colors to the minimum, I predicted that the number of red flowers would greatly outnumber the white flowers within a few generations.
- After simulating several generations, the number of white flowers decreased until the population was entirely red. It took roughly eight generations to get pure red in the population, and this is because the red allele is dominant over the white allele. Even when a flower's genotype is heterozygous (Rr), it will still be red because red is the dominant phenotype. However, white flowers still existed throughout more than just a few generations because two heterozygous flowers could produce a white flower 25% of the time, resulting in a homozygous recessive.

Part B: Select for White

After setting the fitness of white to the maximum and all the other colors to the minimum, I predicted that the number of white flowers would greatly outnumber the red flowers in fewer generations than it took for red, as white flowers should only produce white flowers.
- It only took two generations to get the flower population to be exclusively white, and this is due to the homozygous recessive nature of white flowers. White flowers can only produce white flowers - unlike how red flowers can produce either white or red flowers - so all of the offspring from homozygous recessive flowers will only be white. The reason why it takes more generations to get pure red flowers than it does pure white is because in heterozygous flowers, the white allele is masked by the dominant red allele, resulting in a dominant, red phenotype. However, white flowers may pop up over generations, as two heterozygous flowers could make white offspring 25% of the time.

Part C: Hardy-Weinberg Equilibrium and Natural Selection I calculated the allele frequencies in the starting population of red flowers below:

Genotype	Number	#Rs	#rs
RR	0	0	0
Rr	100	100	100
rr	0	0	0
	Total	100	100

frequency of R (p) = 0.5
frequency of r (q) = 0.5

Next, I calculated the genotype frequencies expected at Hardy-Weinberg equilibrium based off the equation: p^2 + 2pq + q^2 = 1:

frequency of RR = p^2 = (0.5)(0.5) = 0.25
frequency of Rr = 2pq = (2)(0.5)(0.5) = 0.5
frequency of rr = q^2 = (0.5)(0.5) = 0.25

The population of red flowers was not in Hardy-Weinberg equilibrium because rather than seeing 50% of the population be heterozygous, 25% of the population be homozygous dominant, and 25% of the population be homozygous recessive, 100% of the population was heterozygous. A Chi-square calculation derived x2 = 100, which is much higher than the theoretical value of this set, which is 3.841.

After running one generation only, I again calculated the genotype and allele frequencies of the population:

Genotype	Number	#Rs	#rs
RR	27	54	0
Rr	46	46	46
rr	27	0	54
	Total	100	100

frequency of R(p) = 100/200 = 0.5
frequency of r(q) = 100/200 = 0.5
frequency of RR = p^2 = (0.5)(0.5) = 0.25
frequency of Rr = 2pq = (2)(0.5)(0.5) = 0.5
frequency of rr = q^2 = (0.5)(0.5) = 0.25

This population is at Hardy-Weinberg equilibrium.

After setting the fitness of red to the maximum and all the other colors to the minimum, it was predicted that p and q, after several generations, should get closer to 0.5 and thus, eventually reach Hardy-Weinberg equilibrium because red is the dominant phenotype.

After simulating a few generations, I calculated the genotype and allele frequencies of the population:

Genotype	Number	#Rs	#rs
RR	76	152	0
Rr	24	24	24
rr	0	0	0
	Total	176	24

frequency of R(p) = 176/200 = 0.88
frequency of r(q) = 24/200 = 0.12
frequency of RR = p^2 = (0.88)(0.88) = 0.7744
frequency of Rr = 2pq = 2(0.88)(0.12) = 0.2112
frequency of rr = q^2 = (0.12)(0.12) = 0.0144

The results of this portion of the experiment do not match my prediction that throughout generations, the population will stabilize to Hardy-Weinberg equilibrium, though it did match my prediction that the phenotype would be mostly red flowers. Recall, the fitness of red was set to the maximum, so it would make sense for the population to support more RR than Rr and rr.

Conclusions

In Aipotu: Evolution, it was determined that the red allele (R) was dominant over the recessive white allele (r), which is consistent in the findings Aipotu: Genetics revealed. Because red was the dominant phenotype, both homozygous RR and heterozygous flowers appeared red, while homozygous r flowers appeared white. This also plays into the fact that it takes much longer to wipe out white flowers from a population than it does red; heterozygous flowers can cross and produce both red and white offspring, so even though a flower phenotypically is red, it may carry a hidden white allele and produce white offspring later on. In a world where the fitness is maximized to white, however, it only takes two generations to get pure white, as white flowers can only produce white offspring (rr x rr = rr). In terms of Hardy-Weinberg equilibrium, a population is only in such equilibrium when all fitnesses are set equal. In our simulation, when red was set to the maximum fitness, there were little to no white flowers, thus not in Hardy-Weinberg equilibrium. Hardy-Weinberg equilibrium tells us that factors, such as fitness, has an effect on how a population's genetic structure changes over time.

Acknowledgements

I worked with my homework partners Christina Dominguez and Carolyn Egekeze in class for three hours during the lab session and we corresponded via text about using a Chi-Square statistical test.
I copied and modified the procedures from the Evolution simulation of Aipotu in accordance of what I actually did.
I read an article from the University of Tennessee, Knoxville to assist in evaluating whether a population was in Hardy-Weinberg Equilibrium or not.
I utilized Microsoft Excel ToolPak for the Chi-Square test to analyze if the difference in observed versus expected in the Hardy-Weinberg equilibrium equations for Parts C and D were significant.
Except for what is noted above, this individual journal entry was completed by me and not copied from another source.

References

Aipotu. (2017). Aipotu. Retrieved January 23, 2020, from Aipotu.
Hardy-Weinberg Equilibrium (1999). The Institute for Environmental Modeling at the University of Tennesee, KNoxville. Retrieved January 23, 2020, from HARDY-WEINBERG.
OpenWetWare. (2020). BIOL368/S20:Week 2. Retrieved January 29, 2020, from BIOL368/S20 Week 2.

Template

You can access my template for class journals, weekly assignments, and other class-related activities below.

My user page

jennymchua

Template link

jennymchua's template

Class Assignments

Weekly Assignments

Class Journals

Jennymchua Week 2 Assignment

Contents

Purpose

Methods/Results

Methods

Results

Conclusions

Acknowledgements

References

Template

My user page

Template link

Class Assignments

Weekly Assignments

Class Journals

Navigation menu

Page actions

Page actions

Personal tools

Navigation

Search

research

Tools