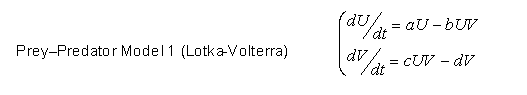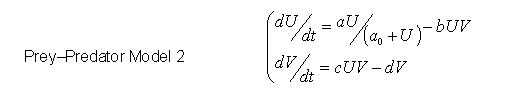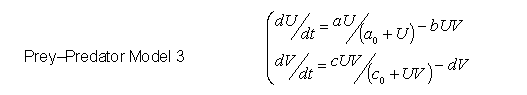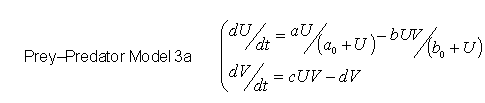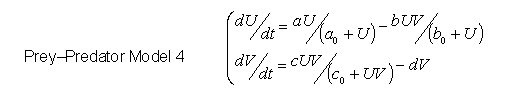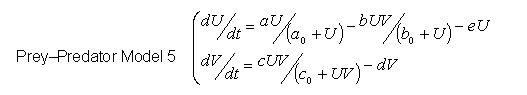IGEM:IMPERIAL/2006/project/Oscillator/Theoretical Analyses/Results
From OpenWetWare
Jump to navigationJump to search
Analysis of the Model of the Molecular Predation Oscillator
Our Results
- During the run of the summer 2006, we had time to study six 2-dimensional Dynamical Systems. Unfortunately we lacked time to carry out a thorough analysis of the 3D model.In order of complexity, the 2D models are:
- 2D Model 1: Lotka – Volterra
- Lotka-Volterra is the first (and most famous) model for prey-predator interactions and is notoriously endowed with some very appealing properties. Lotka-Volterra also was a major inspiration for the design of the molecular predation oscillator.
- 2D Model 2: Bounded Prey Growth
- Lotka-Volterra is far too simple to yield essential results on the complex 2D model.
- We start to investigate the influence of various components of the system by bounding the growth of the preys.
- Detailed Analysis for Model with Bounded Prey Growth
- 2D Model 3: Bounded Predator and Prey Growth
- Bounding the growth of the preys only stabilises the system to the extent we cannot make it oscillate anymore.
- We now seek ways to obtain oscillations by bounding the growth terms of both preys and predators.
- Detailed Analysis for Model with Bounded Growths
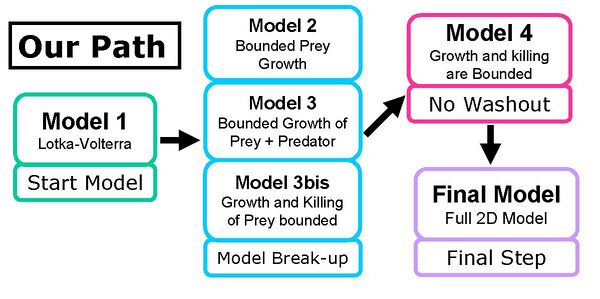
- 2D Model 3bis: Bounded Prey Growth and Prey Killing
- We have studied this model in parallel with Model 3.
- Instead of bounding the production of the predator, we bound the degradation of preys
- In both cases the goal was to investigate whether the various terms of the model could balance each other and yield oscillations.
- Detailed Analysis for Model with bounded prey growth and degradation
- 2D Model 4: Bounded Predator and Prey Growth with Controlled Killing of Preys
- Bounding growth and killing yielded oscillations; bounding prey and predator growths did not.
- We now combine both previous models and get one step closer to the final system
- Detailed Analysis for Model 4
- Final 2D Model : 2D Model 5
- Model 4 can be made to oscillate but also exhibits some very unrealistic properties.
- Fortunately experimental conditions lead us to introduce a final dissipative term –eU to the derivative of the prey population.
- We investigate the properties of this final 2D model and prove that the new dissipative term confers it some very interesting characteristics.
- Detailed Analysis of the complete 2D Model
<html> <!-- Start of StatCounter Code --> <script type="text/javascript" language="javascript"> var sc_project=1999441; var sc_invisible=1; var sc_partition=18; var sc_security="18996820"; </script>
<script type="text/javascript" language="javascript" src="http://www.statcounter.com/counter/frames.js"></script><noscript><a href="http://www.statcounter.com/" target="_blank"><img src="http://c19.statcounter.com/counter.php?sc_project=1999441&java=0&security=18996820&invisible=1" alt="website statistics" border="0"></a> </noscript> <!-- End of StatCounter Code --> </html>
