IGEM:IMPERIAL/2006/project/Oscillator/Theoretical Analyses/Conclusion
Analysis of the Model of the Molecular Predation Oscillator
Conclusion
Overview of our Results on the Molecular Predation System
- We haven't carried out the full study of the 3D model of Molecular Predation System
- Instead we have used some biologically justifiable hypotheses to simplify the model to a 2D model
- We have also carried out a complete theoretical study of the 2D system and are now able to predict for every combination of parameters how the Molecular Predation System will behave.
- In particular we have proved that the Molecular Predation System can operate in two modes:
- - It can work as an oscillator (oscillating around unique limit cycle)
- - It can work in stable regime (both prey and predator populations converge to limit value)
What was learnt from modifying the model
- Oscillations are the results of a subtle balance between the growth terms and degradation terms of the system.
- Oscillations appeared to be mainly due to balancing the growth and degradation terms of the preys
- The washout terms in the model were crucial to control the system
Examples of Oscillations with the Molecular Predation System
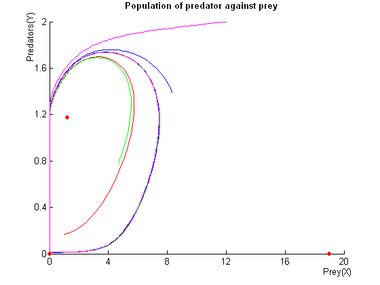
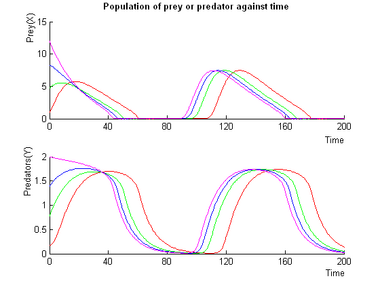
Control of the Oscillations of the Molecular Predation Oscillator
Control of the oscillations is not as simple as with Lotka-Volterra, but simulations show that we have good control over the amplitude and total control over the frequency as shown below.
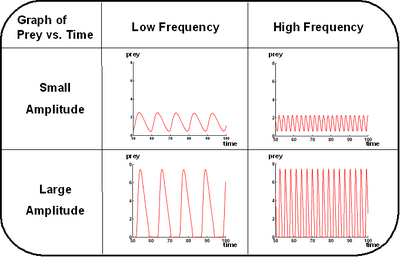
Future Works
Future Works on the 2D Model
- The normalised 2D model of the molecular predation oscillator has been extensively studied.
- Some more work on the oscillator still needs doing however
- The most important work remaining on the normalised 2D model concerns the characterisation of the output of the oscillator with regards to the model parameters
- - Amplitude
- - Frequency
- - Profile (measures of shape in phase diagrams or time diagrams)
- To be complete the characterisation should also be dome with the experimental constraints in mind (e.g: washout cannot be infinitely small)
Extensions to the 2D Model
- The model of the molecular predation oscillator overlooks the leakage terms and does not comprise any exponent in the growth terms.
- With these new terms the dimensionless model would look like
- These assumptions are reasonable a first sight. However, some preliminary results (available in Future Works on the 2D Model) suggest that the oscillator is very sensitive to the assumption on the exponent.
- We therefore suggest carrying out a thorough analysis of the extended model next year
Future Works on the 3D Model
- We only studied the case when d1=d2 and thus simplified the 3D model into 2D
- At the very least the study should be extended to the vicinity of d1=d2
- Ideally the whole 3D system would be studied
- NB: the complexity of the study will increase dramatically
- - Making sure steady points are unstable is not enough
- - We need a solid criterion on how to get a cycle
Stochastic Analysis
- What is the influence of the distributions of gene-expression parameters such as ao,bo,co?
- We may in practice need to drop the Dynamical System approach and go fully stochastic
- An entirely new level of complexity!!!!!
<html> <script type="text/javascript" language="javascript"> var sc_project=1999441; var sc_invisible=1; var sc_partition=18; var sc_security="18996820"; </script>
<script type="text/javascript" language="javascript" src="http://www.statcounter.com/counter/frames.js"></script><noscript><a href="http://www.statcounter.com/" target="_blank"><img src="http://c19.statcounter.com/counter.php?sc_project=1999441&java=0&security=18996820&invisible=1" alt="website statistics" border="0"></a> </noscript> </html>