IGEM:IMPERIAL/2006/project/Oscillator/Theoretical Analyses/Results/2D Model4
From OpenWetWare
Jump to navigationJump to search
Introduction
Generalities
- After proving that bounding both growth and enzymatic degradation of the preys grants the system the capacity to oscillate
- - we now reintroduce the bounded predator growth
- - and check that is does not disturb the balance to the extent that oscillations are impossible again.
- The Dynamical System of Interest in this section is:
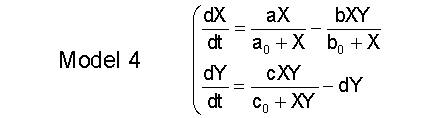
Physical interpretation of the equations
- From a physical point of view the equations are those of the molecular predation system in the absence of chemostat (or equivalently with zero washout).
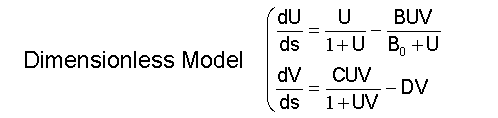
Dimensionless Model
- Since we now have 7 variables , we normalise the system by rescaling the X,Y axes and changing the time scale as we did with model 3, which leaves us with 4 variables only.
- We will use this dimension-less version of the Dynamic System for the rest of the study.
Basic Results on the Steady Points
Number of Steady Points
- The origin (0,0) remains a steady point
- The other steady points of the system are associated to a quadratic equation
- If BC/D<1 the equation yields two admissible steady points
- Else the equation yields only one admissible steady point
Nature of the Steady Points
- The origin (0,0) remains a saddle point
- If BC/D<1 (two admissible steady points)
- - One of them is a saddle point
- - The nature of the other point can be adjusted (from stable to unstable via centre)
- If BC/D is larger or equal to 1 (one steady point)
- - The nature of this point can be adjusted (from stable to unstable via centre)
Behaviour at Infinity
A New Explosive Mode
- We could not prove simply that the trajectories remained bounded as time goes to infinity.
- Simulations quickly showed this was a hopeless effort
- For a combination of parameters trajectories are not bounded!!!
Case 1: When BC/D < 1 (the system has 3 steady points)
- trajectories are not bounded
- the predator population converges to a steady value D/C
- this predator population is too low to repress the prey population
- the prey population diverges to infinity
Case 2: When BC/D>=1 (the system has 2 steady points)
- trajectories remain bounded and spin around the second steady point
- we can apply Poincare-Bendixson
- consequently
- - when the point is stable, the system stabilises itself at the steady point
- - else we have oscillations around the steady point
Summary of the Results
- It follows from the results stated above that the system has three different modes
- Prey Explosion
- Stability
- Oscillations
Typical Simulations
First Mode: Prey Explosion
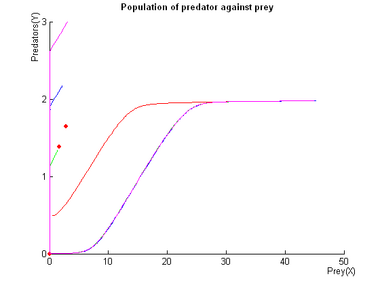
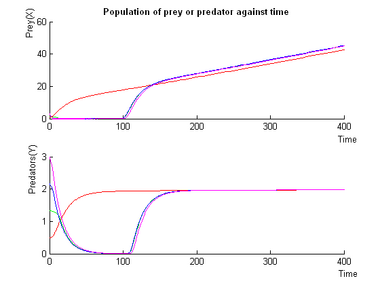
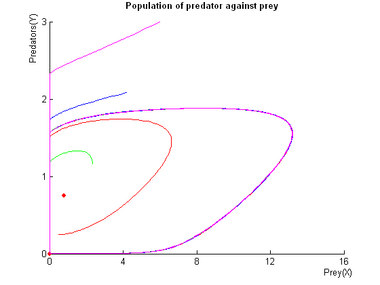
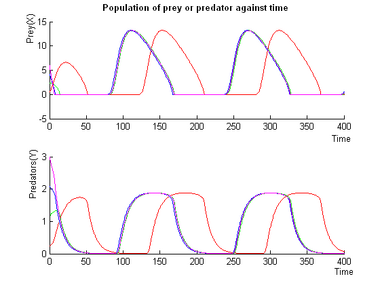
Second Mode: Oscillations
Last Mode: Stability
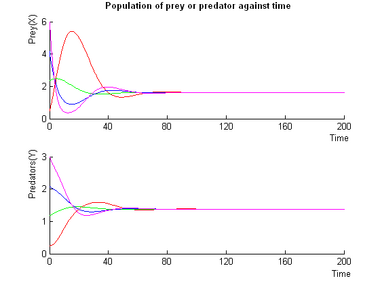
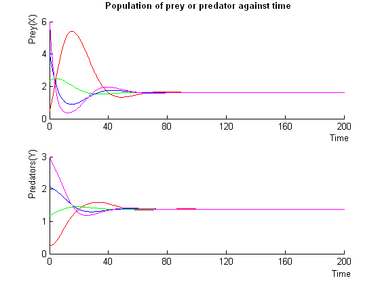
- Note on the Simulations:
- Simulations using different initial conditions are assigned different colors (the open-end of the trajectories is the starting point).
- In the phase diagrams , red dots symbolise a steady points.
Conclusion
- Bounding the predator growth has not removed the capacity of the system to oscillate on a unique limit-cycle.
- However, it has introduced a new dangerous (and highly unrealistic) mode where the prey population explodes.
- Fortunately a final modification still needs introducing: the use of a chemostat in our final construct. The chemostat is used to keep the ratio of cells constant primarily, but also to get rid of any excess in the system. It is hoped that this regularising behaviour will help stabilise the system enough to eliminate the 'explosion' mode.
Appendices
- A more detailed analysis of the system was made by Matthieu. Please consult it if you have any questions on the results on this page.