Davidson:Davidson iGEM 2006
 http://www.davidson.edu Project Overview Davidson Parts Team Members Tools and Resources Check out our Official Team Photo NEW Davidson's Awards and Photo Gallery from iGEM Jamboree 2006 |
 |
Solving the Pancake Problem with an E. coli Computer
| |
| Our goal is to genetically engineer a biological system that can compute solutions to a puzzle called the burnt pancake problem. The E.HOP computer is a proof of concept for computing in vivo, with implications for future data storage devices and transgenic systems. Our work was done in collaboration with the Missouri Western iGEM Team and an undergraduate research fellow from Hampton University. | 
|
The Burnt Pancake Problem
| The pancake problem is a puzzle in which a scrambled series of units (or stack of pancakes) must be shuffled into the correct order and orientation. You can try solving a simple version of the pancake problem yourself. In the burnt pancake problem, each pancake is given an orientation by burning one side. To solve the problem, every unit, or pancake, must be placed in the proper order (largest on bottom, smallest on top) and in the proper orientation (burnt side down, golden side up). The pancakes are flipped with two spatulas: one to lift pancakes off the top of the stack, the other to flip part (or all) of the remaining stack of pancakes. The pancakes lifted by the first spatula are returned to the top of the stack without being flipped. Figure 1 illustrates how the puzzle is solved. |
 |
Approach
| Trial and error is one approach to solving the burnt pancake problem, but how could one compute the quickest solution? Our idea is to let E. coli do the work, using each cell as a tiny processor in a massively parallel machine. A mathematical model of the flipping process helps us design the system and interpret the output of our EHOP computer. |
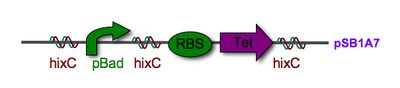
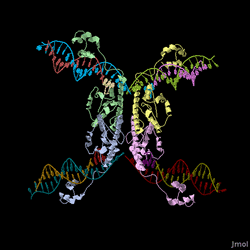 Every segment of DNA flanked by a pair of HixC sites is a "pancake" capable of being inverted. Hin invertase recognizes pairs of HixC sites and inverts the DNA fragment in between the two HixC sites with the help of the Fis protein bound to the RE. In our system, selectable phenotypes (including antibiotic resistance and RFP expression), depend upon the proper arrangement of a series of HixC-flanked DNA segments in a plasmid. This allows us to select for cells that have successfully solved the puzzle. An example of a sorted stack of two pancakes is shown in Figure 3. There are 7 other configurations of 2 pancakes. If we increase the number of pancakes to 4, there are 384 configurations. In general, there are 2n n! configurations of n pancakes, a combinatorial explosion of possibilities. How many should we build and test? Which ones are most informative? We need a mathematical model to help answer this question. |
 Mathematical Model: Our mathematical representation of a stack of pancakes is a signed permutation, in which each numerical value represents the pancake size and the sign of the number represents the orientation. For example, (1, 2, 3, 4) is a sorted stack of four pancakes, all in the proper order and orientation, and (-2, 4, -1, 3) is the scrambled stack of four pancakes shown on the far left of Figure 1. Note that pancakes 1 and 2 are negative, indicating that these two pancakes are in the wrong orientation (burnt side up). 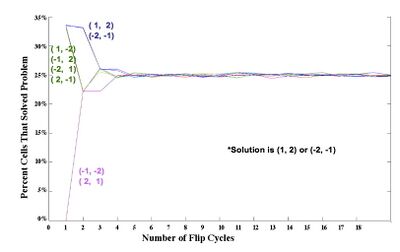 From these simulations, and similar results for stacks of 3 and 4 pancakes, we discovered that the probability of a plasmid being sorted after k flips was determined by how many ways the solution could be obtained. Several initial configurations had essentially the same graph in our simulations because they had the same number of ways of being sorted. Only one representative from each of these "families" of initial configurations needs to be built and tested. |
| Methods and Results The following is an outline of what the Davidson team will present at iGEM 2006 | |||
| Basic parts Parts used in this project were designed by two iGEM Teams Modeling
|
Building the Biological System
|
Conclusions
| |
Students
- Sabriya Rosemond is a junior biology major at Hampton University.
- Erin Zwack is a junior biology major at Davidson College.
- Lance Harden is a sophomore math major at Davidson College.
- Samantha Simpson is a sophomore at Davidson College who might design a major in genomics.
Faculty
- A. Malcolm Campbell Department of Biology
- Laurie J. Heyer Department of Mathematics
- Karmella Haynes Department of Biology - teaching postdoc and visiting assistant professor
| iGEM 2006 Jamboree |
White Board |
Assembly Plans |
Progress |
| Wet Lab Tools |
Simulators
|
Graphing Tools |
Miscellaneous Computation Tools |