Cameron M. Rehmani Seraji Week 5

From OpenWetWare
Jump to navigationJump to search

Cameron M. Rehmani Seraji Week 5

Cameron M. Rehmani Seraji

Purpose

  • The purpose of this assignment was to work with the nutrient models from the Week 4 assignment more, to understand how to solve differential equations by hand and what those equations mean, and to also realize that some models are better fits for the question being asked.

Methods

Part 1

  • Looked at the definition of model one and determined that it would not work for a system with two nutrients.

Part 2

  • Worked out the algebra and determined that the three equilibrium equations were correct for the three different equations.
  • My work can be seen in the link in part 2 of the results section.

Part 3

  • The work for finding the calculations for the different equilibrium values is shown in figure 1(a), 1(b), and 1(c).

Figure 1(a): Page 1 of equilibrium calculations. Figure 1(b): Page 2 of equilibrium calculations. Figure 1(c): Page 3 of equilibrium calculations.

Part 4

  • I compared the equations for model two and model three. I used my work for finding the equations for model two as a guide to find the equations for part three.

Results

Part 1

  • Explain why Model One, the additive model, may not be the best choice.
    • Model One, the additive model, is not the best choice because the additive model is a type of "or" model meaning that if one of the nutrients were to go to zero, the yeast reproduction would be maintained in the presence of the other nutrient. This would not work for yeast because yeast requires glucose and ammonia in order to grow. For example, if the glucose were to run out, yeast reproduction would not be maintained by the presence of ammonia.

Part 2

  • Work out the algebra to show that Model Two's "non trivial" equilibrium is characterized by the equations below, for yeast, residual ammonium, and residual glucose, respectively.
    • The work for the model two "non trivial" equilibrium equations for yeast, residual ammonium, and glucose is in the link below.

Figure 2: Model Two's "non trivial" equilibrium equations

Part 3

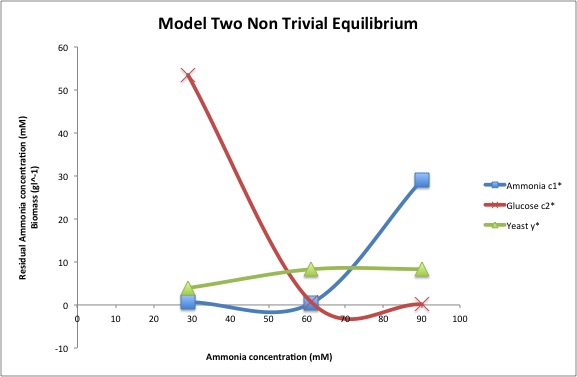
  • Set q=0.15, V1=110, V2=180, K1=2.5, K2=10, R=15, and U2=100. With these values, and the values of U1 in the journal club paper for ammonium feed concentrations, find the equilibrium values of yeast, residual ammonium, and residual glucose. Recreate the journal club paper Figure 1(a) plot with your findings.
    • The equilibrium values of yeast, residual ammonium, and and residual glucose when u1 has values of 29, 61, and 90 is shown in the graph below.

Part 4

  • Are there analogous equations to the ones of Part (2) for Model Three? If so, what are they?
    • Analogous equations to the ones of part 2 were found for model three. The equations and the work of how they were found can be found in the link below.

Figure 3: Model Three Equilibrium Equations

Scientific Conclusion

  • The additive model for nutrients is not a good model for yeast growth because yeast growth requires both ammonium and glucose. Next, using the multiplicative nutrient model, a graph of equilibrium values of yeast, residual ammonium, and residual glucose was generated. In the graph, as the concentration of ammonium increases, the residual ammonia concentration increases, the residual glucose concentration decreases, and the equilibrium of yeast remains relatively constant. Lastly, the rate limited nutrient use model is similar to the multiplicative nutrient model, so analogous equilibrium equations can be generated.

Acknowledgements

References

Navigation Links

Retrieved from "https://openwetware.org/mediawiki/index.php?title=Cameron_M._Rehmani_Seraji_Week_5&oldid=974443"