Biomod/2011/Harvard/HarvarDNAnos:Results Sphere
<html> <head>
<style>
- column-one { display:none; width:0px;}
.container{background-color: #f5f5f5; margin-top:50px} .OWWNBcpCurrentDateFilled {display: none;}
- content {width: 0px; margin: 0 auto auto 0; padding: 1em 1em 1em 1em; align: center;}
- column-content {width: 0px; float: left; margin: 0 0 0 0;padding: 0;}
.firstHeading {display:none; width:0px;}
- globalWrapper{width:1280px; margin:auto}
body {background: #F0F0F0 !important;}
- column-one {display:none; width:0px;background-color: #f0f0f0;}
- content{border:none;margin: 0 0 0 0; padding: 1em 1em 1em 1em; position: center; width: 800px;background-color: #f0f0f0; }
.container{ width: 800px; margin: auto; background-color: #f0f0f0; text-align:justify; font-family: helvetica, arial, sans-serif; color:#f0f0f0; margin-top:25px; }
- bodyContent{ width: 1267px; align: center; background-color: #f0f0f0;}
- column-content{width: 1280px;background-color: #f0f0f0;}
.firstHeading { display:none;width:0px;background-color: #f0f0f0;}
- header{position: center; width: 800px;background-color: #f0f0f0;}
- footer{position: center; width:1280px;}
</style>
</head> </html>
<html>
</html>
Spherical Container
...Return to Results <html> </html> Go to Methods...<html> </html> Go to Design...
Overview
With our sphere design, we were able to:
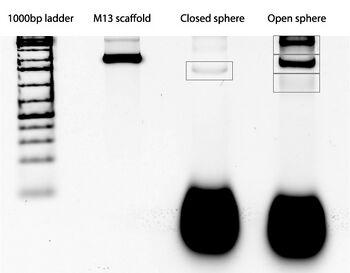
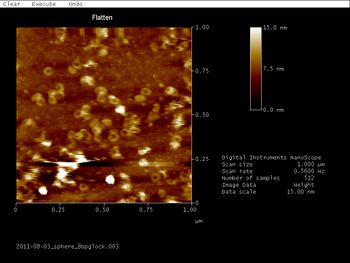
- Fold and characterize through atomic force microscopy (AFM) the original Han et al. sphere, which we call the "closed" sphere.
- Fold and characterize through AFM our "open" sphere in which we removed all equator staple strands.
- Test various lock mechanisms to transition between the closed and open states of the sphere.
- Analyze the scaffold-staple-lock system to find out why certain lock designs were unsuccessful at closing the sphere.
Note that due to the sphere being a single-layer DNA structure and a popular shape for water droplets, it was hard to characterize via transmission electron microscopy.
Folding Origami
Gel
Closed Sphere
Opening the Sphere
Open Sphere
Closing the Sphere
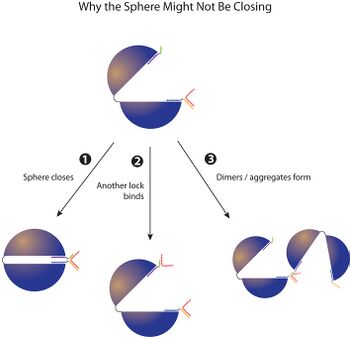
We tested a variety of locks to close the open state of the sphere, changing lock length, composition, and concentration relative to open spheres. Unfortunately, the AFM images we obtained all indicated that these spheres were still in an open state.
Troubleshooting
We also explored the kinetics of scaffold, staple, and lock interaction for this system to see whether Scaffold:Staple complexes or Staple:Lock complexes form first.
- Calculations of which interaction, Scaffold:Staple or Staple:Lock, will ultimately win out:
- There are 100 nM of any individual staple and 10 nM of scaffold in solution. Assume the concentration of lock is 900 nM; because there are 9 locks per sphere, this actually means the lock is the same concentration as an individual staple. The reaction that proceeds is:
- Scaffold + Staple --> Scaffold:Staple
- At Tm1, the melting temperature of the Scaffold:Staple complex, there are 5 nM of Scaffold:Staple, 5 nM of Scaffold, and 95 nM of Staple.
- [math]\displaystyle{ K_{eq}=\frac{[Scaffold:Staple]}{[Scaffold][Staple]} = \frac{5 nM}{5 nM*95 nM} = \frac{1}{95 nM} = 10^7 / M }[/math]
- There are 100 nM of any individual staple complementary to the lock and 900 nM of lock in solution. The reaction that proceeds is:
- Staple + Lock --> Staple:Lock
- At Tm2, the melting temperature of the Staple:Lock complex, there are 50 nM of Staple:Lock, 50 nM of Staple, and 850 nM of Lock.
- [math]\displaystyle{ K_{eq}=\frac{[Staple:Lock]}{[Staple][Lock]} = \frac{50 nM}{50 nM*850 nM} = \frac{1}{850 nM} = 10^6 / M }[/math]
- At melting temperature Tm,
- [math]\displaystyle{ \Delta G^{\circ}=-R T_m \log{K_{eq}}=\Delta H-T_m \Delta S }[/math]
- [math]\displaystyle{ T_m=\frac{\Delta H^{\circ}}{\Delta S^{\circ}-R \log{K_{eq}}} }[/math]
- Assuming that ΔH° and ΔS° are approximately the same for Scaffold:Staple and Staple:Lock interactions, a larger (more positive) Keq results in a larger numerator in the expression above. Since ΔS° is negative, a larger Keq results in a more negative Tm.
- So, since Keq is larger for the Scaffold:Staple reaction, Tm is lower for the formation of Scaffold:Staple than for Staple:Lock. In other words, when temperature is being lowered in the thermocycler, Staple:Lock forms before Scaffold:Staple.
From these calculations we can conclude that adding a high concentration of lock may not help the open spheres close.
To avoid the problem of locks not dislodging once bound to a staple, we designed shorter locks that have complementary regions of ~8 bp rather than ~16 bp. This shorter complementary sequence allows locks and staples to periodically dissociate, meaning scenarios (2) and (3) in the above diagram are not permanent.
We tested these "8 bp locks" but did not see conclusive evidence of open spheres closing. However, we believe that with additional time it is entirely possible to design a system of locks that will close the open sphere.