Asymmetric Flow Patterns - Sara Bruni

Background

Mixing is a process in which one immiscible liquid is incorporated into another immiscible liquid. In microfluidics, the goal is to achieve a thorough and rapid mixing within devices. These mixing schemes can be described as active or passive. Active mixing is characterized by an external energy source to achieve mixing, while passive mixing occurs in the absence of additional energy. Passive mixing uses different microchannel configurations to restructure the flow and induce mixing. Asymmetric flow patterns include different methods of active and passive mixing used to speed up the mixing process at the microscale. In order for mixing to occur, flow patterns must be asymmetric. This section will focus on the different methods of asymmetric active and passive mixing.

Mixing on the Microfluidic Scale

Microfluidic systems and devices are becoming more common in a variety of applications and are revolutionizing the biomedical and drug development industries. In standard macroscale systems, mixing is achieved through turbulent flow. Due to the scale of these microfluidic systems, turbulence is not attainable as a result of the low Reynolds numbers. Reynolds number is the relationship between inertial forces and viscous forces within a system.

Figure 1: Laminar flow within a microfluidic channel. Slow diffusion occurs at each interface. Reprinted figure with permission from Kenis, P. J. A., Ismagilov, R. F., Whitesides, G. M. Microgavrication Inside Capillaries Using Multiphase Laminar Flow Patterning, "Science", 1999; pp 83-85. Copyright Sience 1999. DOI: https://doi.org/10.1126/science.285.5424.83

Reynolds number is found using the following equation:

[math]\displaystyle{ \mathrm{Re} = \frac{\rho v L}{\mu} }[/math],

where

• [math]\displaystyle{ \rho }[/math] is the density of the fluid,
• v is the velocity of the fluid,
• L is the characteristic length of the fluid,
• [math]\displaystyle{ \mu }[/math] is the dynamic viscosity of the fluid.

Laminar Flow

Laminar flow is characterized by a Reynolds number less than 2,000. In this flow pattern, parallel lines flow linearly and there is an absence of mixing. In a microfluidic system, the characteristic length dominates the equation and leads to a low Reynolds number. Flow within microfluidic systems is laminar, and since there is no turbulence in these systems, mixing relies solely on diffusion which is a very slow and inefficient process. The goal of these microfluidic mixing patterns is to promote mixing through different means, like introducing additional forms of energy through active mixing such as magnetic stirring or acoustic micro-mixing

Methods of Active Mixing

Figure 2: Magnetic stirring apparatus consists of the liquid, the stirrer magnet, the drive magnet and the magnetic drive. Reprinted figure from public source BOLA, https://www.bola.de/en/technical-information/stirring-and-mixing/stirrer-magnetic-stirring/

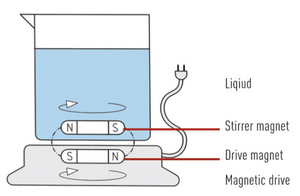
Magnetic Stirring

Magnetic stirring is an active mixing method which utilizes a magnetic stir bar and a rotating magnet to conduct mixing. The stir bar is placed into the liquid and its motion is driven by another rotating magnet in the device beneath the vessel containing the liquid. Magnetic mixers are often seen in laboratories, and in microfluidics, they are on a smaller scale. This method of mixing achieves rapid mixing without additional wires intruding the system. However, problems arise in regard to the stir bar length, as mixing does not extend very far past the end of the stir bar. Designing a stir bar of optimal length or using multiple stir bars can help to solve this problem.

The advantages of using the magnetic stir bar consist of rapid mixing within the length of the bar, no external interfacing due to the applied external magnetic field, and the ability to mix a wide variety of liquids.

The disadvantages to using the magnetic stir bar revolve around the assembly of the device. The magnetic stir bar requires multiple fabrication steps and a separate integration of mixer. The planar geometry also restricts mixing in the vertical direction.

Acoustic Micro-Mixing

Figure 3: Diagram of acoustic micro-mixing induced by an air bubble on a solid wall. Reprinted figure with permission from Liu, R. H., Yang, J., Pindera, M. Z., Athavale, M., Grodzinski, P. Bubble-induced acoustic micromixing. "Lab on a Chip". 2002; 2, pp 151-157. Copyright 2002 Royal Society of Chemistry DOI: https://doi.org/10.1039/B201952C

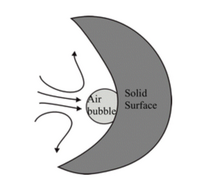
Acoustic Micro-Mixing (AMM) is a method of active mixing which uses sound waves to promote mixing and increase the rate of diffusive mixing. Bubble induced acoustic micro-mixing uses an air bubble in the liquid.

This bubble is then exposed to vibration through sound waves, which generates frictional forces around the bubble and produces strong liquid circulation flow. This method of mixing can also significantly reduce mixing times from 6 hours to 1.75 minutes.

This application uses a single apparatus that is easy to implement and has low power consumption which contributes to its low cost. Another advantage of acoustic micro-mixing includes its relatively low strain field.

The disadvantages to acoustic micro-mixing consist of the difficulty to fabricate and integrate the device into microfluidic systems. There are limitations to how small the mixing chamber can be in the device. Additionally, the performance of the device is sensitive to bubble size.

Pneumatic Valves and Mixers

Pneumatic valve and mixer systems are another method of active mixing through liquid manipulation on the microfluidic scale. These valves apply pressure to the membrane which actuates liquid flow and are a common type of microvalve controlled by gas pressure. They can be grouped and synchronized to work as pumps or mixers and achieve different forms of liquid flow. This flow method is widely used in microfluidics since it is easy to integrate into different systems.

One of the downsides to these systems is that these microvalves are overly sensitive to the specific device configuration and pressure values, making their application limited in certain fields. They are widely used in drug discovery and cell analyses.

Back and Forth

The Back and Forth mixing method involve asymmetric mixing patterns that can stretch and fold. The laminar flow is reversible within the limits of diffusion. Mixing can only occur through diffusional broadening, however, there is no benefit from reversed flow. When utilizing Back and Forth mixing method, it is crucial for the user to carefully design the pattern flow.

Methods of Passive Mixing

Figure 4: Schematic showing mixing cycles due to the asymmetry of the chevrons within the staggered herringbone device. Centers of rotation are indicated by "c", where areas of upwelling and downwelling are labeled by "u" and "d" respectively. (a) Fluorescent confocal images showing mixing after half and a full cycle. (b) Reprinted figure with permission from Stroock, A. D., Dertinger, S. K. W., Ajdari, A.; Mezic, I., Stone, H. A., Whitesides, G. M. Chaotic Mixer for Microchannels. Science. 2002; 295(555), pp 647-51; DOI: https://doi.org/10.1126/science.1066238

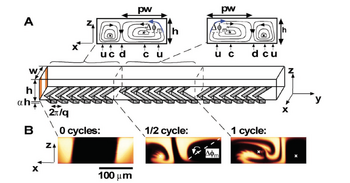
Herringbone Mixer

The Herringbone Mixer is a mixing cycle that is composed of two sequential ridges in which the direction of asymmetry of the herringbone switches with respect to the centerline of the channel. Resembling the bones of a fish skeleton, its distinctive V-shaped pattern allows for transverse velocity components which induces helical trajectories. An off-centered herringbone pattern can be used to improve the mixing between loops. The fluid can become stretched and folded over itself to reduce the path for diffusional mixing. The Herringbone Mixer can be quantified through the achievable mixing length of the channel, the diffusional length at that position along the channel, and the initial diffusional length. The length of the channel to achieve mixing, [math]\displaystyle{ \Delta y_m }[/math], is

[math]\displaystyle{ \Delta y_m \sim U \times (\Delta r)^2/D }[/math],

where

• [math]\displaystyle{ \Delta y_m }[/math] is the length of the channel to achieve mixing,
• U is the average linear velocity,
• [math]\displaystyle{ \Delta r }[/math] is the diffusional length at position [math]\displaystyle{ \Delta y_m }[/math] along the channel,
• D is the diffusion coefficient.

The diffusional length, [math]\displaystyle{ \Delta r }[/math], can be defined as

[math]\displaystyle{ \Delta r = l \exp(-\Delta y_m /\lambda) }[/math],

where

• [math]\displaystyle{ l }[/math] is the initial diffusional length (straight channel),
• [math]\displaystyle{ \lambda }[/math] is the Liapunov exponent or the characteristic length determined by the geometry of trajectories in chaotic flow.

Therefore, the uniform and homogenous mixing is

[math]\displaystyle{ \Delta y_m \sim U \times l^2/D = \mathrm{Pe} \times L }[/math].

This can be related to the length for large Peclet number as follows:

[math]\displaystyle{ \Delta y_m \sim \lambda \ln{(\mathrm{Pe})} }[/math].

Twists and Bends

Figure 5: Schematic of the three-dimensional serpentine channel (top). Schematic of the square-wave channel (middle). Schematic of the straight channel (bottom). Reprinted figure with permission from Liu, R. H., Stremler, M. A., Sharp, K. V., Olsen, M. G., Santiago, J. G., Adrian, R. J., Aref, H., Beebe, D. J. Passive Mixing in a Three-Dimensional Serpentine Microchannel. Journal of Microelectromechanical Systems. 2000; 9(2), pp 190-197; Copyrighted 2000 Institute of Electrical and Electronics Engineers. DOI: https://doi.org/10.1109/84.846699

The incorporation of twists and bends can generate chaotic advection. The advection criterion is as follows:

• For square-wave channels, the Reynold’s number must be greater than 70 (Re > 70),
• For a fixed channel length, the Reynold’s number must be equal to 70 (Re = 70),
• For a serpentine mixer, the Reynold’s number must be greater than 6 (Re > 6).

While the square-wave channels allow for 10 times more mixing, the serpentine mixer allows for 16 times more mixing in comparison to the fixed-channel length. The serpentine mixer’s higher characteristic velocity scale allows for the mixer to undergo higher velocity and mixing capabilities than square-wave mixers.

Recirculating Plugs

Recirculating plugs create a plug of one liquid phase that typically contains species to be mixed inside of another immiscible phase. There are no-slip conditions at the walls which forces the liquid inside the plug to move. The Liquid-Liquid interfaces, where two immiscible liquids meet, are constrained in order to force the liquid to re-circulate. Asymmetry is located at the walls of the channel which induces different sized re-circulating regions. Chaotic advection changes the flow within the drop using the geomtry of the channel to mix the content of the drop while maintaining laminar flow.

Droplets

Droplets can move through microfluidic channels while maintaining their original solute concentration within the droplet. Typically, droplets are used to contain multiple reagents or merge droplets containing reactants. It is a challenge to control the rate at which the components mix within the droplets. Without any applied mixing strategies, the components within droplets will mix at the rate of diffusion. A droplet moving within a straight microchannel will use forces generated by movement to create a hemisphereic recirculating flow within the droplet.

The serpentine path assists in the recirculating of flow to improve the mixing relative to diffusion and maintain the areas of low flow. Currently, the most rapid and effective mixing can be achieved by controlling the droplet size and the orientation of bends and patterns in the channel. Step-emulsification, a method to produce monodisperse droplets, uses the geometry present to acheive a high production of droplets. It can offer homogenous droplets with high-dispersed phase ratios as induced by the device geomtrey and interface instabilities.

Applications

Figure 6: Optical micrograph of a microfluidic chip capable of mixing lipids and aqueous protein solutions between the chambers and the injection valved on the top of the three large chambers. Reprinted figure with permission from Perry, S. L., Roberts, G. W., Tice, J. D., Gennis, R. B., Kenis, P. J. A. Microfluidic Generation of Lipidic Mesophases for Membrane Protein Crystallization. Crystal Growth & Design. 2009; 9(6), pp 2566-2569. Copyright 2009 American Chemical Society. DOI: https://doi.org/10.1021/cg8008688

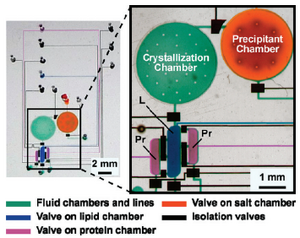
The utilization of asymmetric flow patterns can be observed in the methodology of screening suitable crystallization conditions of membrane proteins. Side chambers are asymmetrically arranged to enable offset fluid injection into the center chamber of an integrated microfluidic chip. A tendril-whorl type flow mixing is present at each point of injection in which chaotic mixing is done by stretching and folding the two fluid components until the length scale of the individual lamellae is on the order of the diffusion length. The tendril-type flow occurs as the fluid stretches upon moving from one fluid chamber to another through injection channels. The whorl-type flow occurs as the fluid leaves the injection channels and enters a fluid chamber where it folds around and is enhanced when fluid enters a chamber from multiple injection lines.

Achieving mixing within a microfluidic system is essential for a variety of applications, like increasing the rate of reaction. When compared to passive mixing methods, active mixing offers better control over the rate of mixing and the level of mixing. The plethora of active mixers available also provides a suitable option for many different systems.