Alondra Vega: Week 4

Terminology

The Michaelis-Menten equation describes the relationship between the rate of a substrate conversion by an enzyme to the concentration of the substrate in the equation. V is the rate of conversion, [S] is the substrate concentration and K_m is the Michaelis constant. K_m approximates the affinity of enzyme for the substrate.
The Lineweaver-Burk experiment shows a way of illustrating kinetic date. The plot is produced by taking the reciprocal of the Michaelis-Menten equation. It will usually produce a linear function y = mx + b.
A chemostat reaction deals with the flow rate into the system and the flow rate out of the system. A mathematical model is used (a set of differential equations) to see the change in the steady state, or to find what the steady state is.
Exponential growth (including exponential decay) occurs when the growth rate of a mathematical function is proportional to the function's current value. It will produce a similar curve to e^x when plotted.

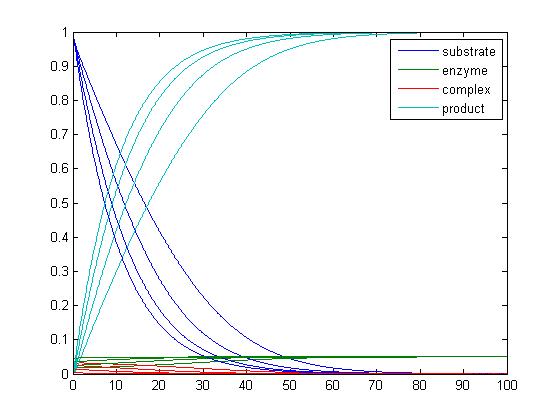
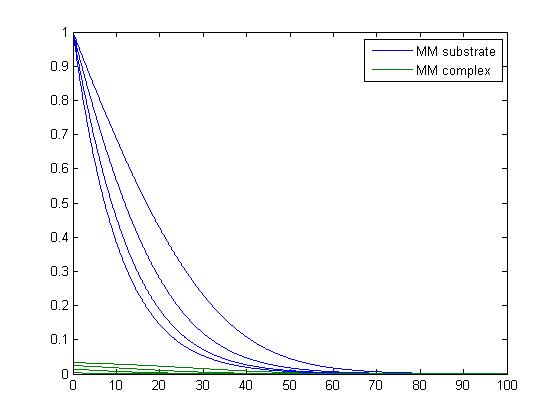
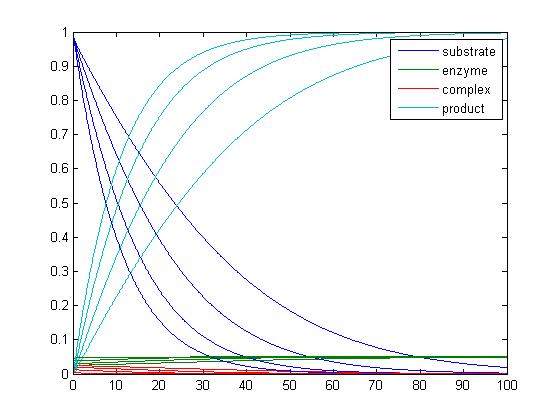
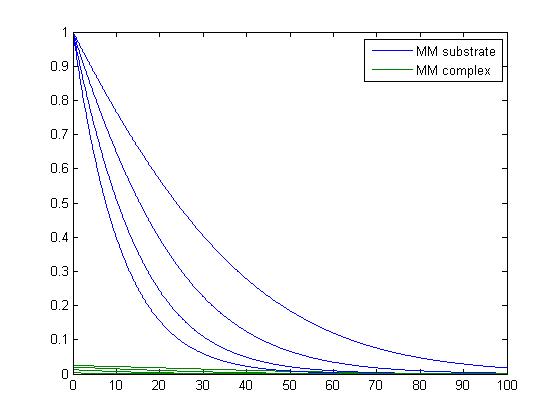
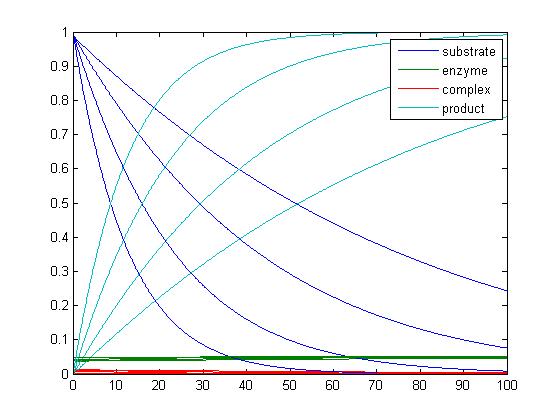
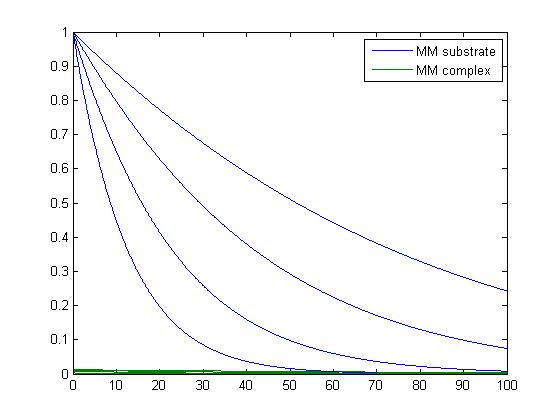
In was not sure what was being asked when working with this code. I was not sure what program I was supposed to use. I used the michaelis_menten, catalysis and catalysis-driver. I am not sure what the differences are between catalysis and the Lineweaver-Burke program, so I stayed with the program that we worked on last week, since i do not feel that we went into depth the other program. I also do not know what the graphs are saying. I feel that I would have been able to compare them better if they were not all in the same plot. I would have been able to see which belong to which k_-1 value. I know that there are settings to differentiate between the graphs, but I have not mastered those skills yet. The graphs provided below show the graphs that the catalysis driver produces.
When k_-1=0.

After working on excel with the Lineweaver-Burke technique with the given points, I found that V_max was 0.031551 and K was 27.10932. Vmax is found was by taking the inverse of the y-intercept on the trendline that we added on the graph. the K value was found by taking the slope of the line and dividing it by the intercept.