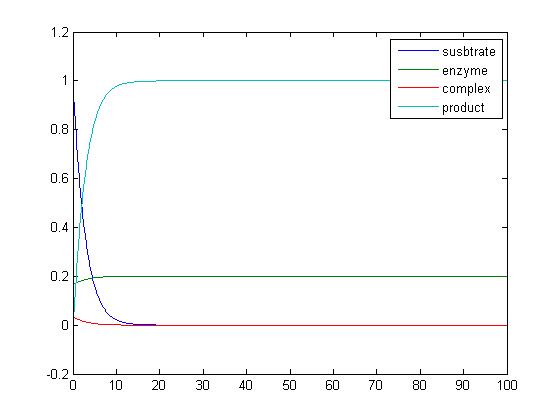
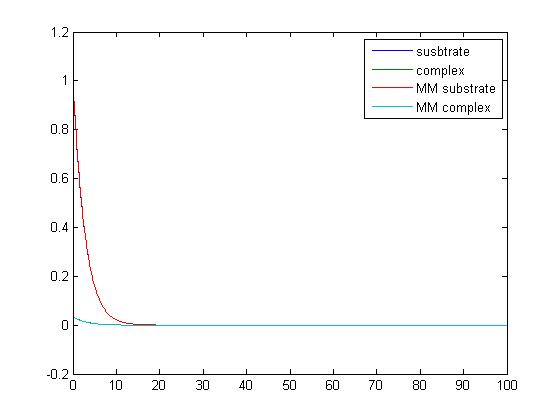
Alondra Vega: Week 3
From OpenWetWare
Jump to navigationJump to search
Terminology
- dynamical system:A space together with a transformation of that space, such as the solar system transforming over time according to the equations of celestial mechanics.[1]
- law of mass action:The law that states the following principle: the rate of a chemical reaction is directly proportional to the molecular concentrations of the reacting substances.A law stating that the intensity of a reaction is dependent on the degree of presence of the reactants responsible for the reaction.[2].
- homeostasis: The ability of the body or a cell to seek and maintain a condition of equilibrium or stability within its internal environment when dealing with external changes. [3]
- equilibrium:The condition in which all acting influences are balanced or canceled by equal opposing forces, resulting in a stable system. (no net change in terms of substrate and products)[4]The rate of the forward reaction = the rate of the backwards reaction.
- oscillation:Fluctuation; variation; change back and forth.[5]
- autocatalysis(autoactivation):a reaction in which one or more of the products formed acts to catalyze the reaction; beginning slowly, the rate of such a reaction rapidly increases.[6]
Applying the Law of Mass Action
Instructions:* Construct differential equations that model the following reactions. Be sure to define your state variables and rate constants.
- A + B → C
- A + B ↔ C
- A + B ↔ 2C
- 2A + 3B ↔ C+D
Please note that the symbol ↔ is used to denote arrows (reactions) in both directions.
- For the first reaction, we know that it only has one direction. This means that both A and B are changing C, but not the other way around. Thus, we would only have one differential equation describing how C is changing.
- d[C]/dt = k1[A][B]
- For this second reaction, we know that it goes both directions. This means that both A and B are changing C. Also, by using the constant k-1, C will also have an effect on A and B. Thus we have three differential equations that describe how these elements are changing over time.
- d[C]/dt = k[A][B], which describes how C is changing in respect to the concentration of A and B.
- d[A]/dt = -k1[A][B]+k-1[C], which shows how much of A is lost when producing C and how much is gained in the reverse reaction.
- d[B]/dt = -k1[A][B]+ k-1[C], which shows how much of B is lost when producing C and how much is gained in the reverse reaction.
- For the third reaction, we know that it goes in both directions. When looking for the differential equation for the rate of change of C, we must divide the entire reaction by 2, since we are looking for the rate of C. When working with the differential equation for A and B, the 2 in front of the C will act as an exponent on he concentration.
- d[C]/dt = k[A]1/2[B]1/2, which shows how C is produced.
- d[A]/dt = -k1+k-1[C]2, which shows how A is lost and produced.
- d[B]/dt = -k1+k-1[C]2, which shows how much B is lost and produced.
- This last reaction has similar properties as the previous reaction.
- d[C]/dt = k-1[A]2[B]3-k1[C][D], which shows how C is changing in both reactions.
- d[D]/dt = k-1[A]2[B]3-k1[C][D], which shows how D is changing in both directions.
- d[A]/dt = k1[C]1/2[D]1/2-k-1[B]3/2[A], which shows how A is changing in both directions. Notice that to find this rate, the entire reaction was divided by two.
- d[B]/dt = k1[C]1/3[D]1/3-k-1[A]2/3[B], which shows how B is changing in both directions. Notice that to find this differential equation, the entire reaction was divided by 3.