Taylor Dispersion - Diwakaran RP
Introduction
As we go down to the microscale, laminar flow becomes more dominant, and diffusive mixing becomes more apparent (referred as diffusional broadening) than when compared to macroscale flow systems where convective mixing is heavily dominant. laminar flow is usually characterized by well-defined streamlines that do not cross each other, which means no lateral mixing due to convection. Turbulent flow on the other hand has chaotic flow patterns leading to a convectively dominant mixing. Therefore, when in the laminar flow region we can predict the diffusional mixing using Fick's law and this lets us determine the movement of solutes or other dispersing species in a continuous media. One specific case of diffusional broadening is discussed here. [7]


When a liquid plug is pushed through a channel, the flow in laminar region, the plug gets sheared due to the parabolic velocity profile and this increases the effective diffusivity of the species. This phenomenon was named after Sir. G.I.Taylor, who observed this shear-induced dispersion inflows with large Péclet numbers ([math]\displaystyle{ P_{e} = uL/D }[/math]) and this phenomenon was generalized for arbitrary Péclet numbers and studied in detail in by Rutherford Aris . And sometimes, this phenomenon is also known as the Taylor-Aris Dispersion. [1-3]
Taylor-Aris Dispersion
To understand the phenomenon of Taylor dispersion, it is helpful to visualize a strip of colored species being pumped through a clear liquid (see Video 1) which is driven by a pressure gradient. The colored species and the clear liquid start to move under two driving forces, the pressure difference and the concentration gradient. Looking at these two driving forces separately, the pressure-driven flow causes both the liquid and the colored species to have a parabolic velocity profile, and the concentration gradient between the colored species and the liquid causes the species to diffuse into the liquid (and sometimes vice versa). The superposition of these two effects produces the Taylor-Aris dispersion.
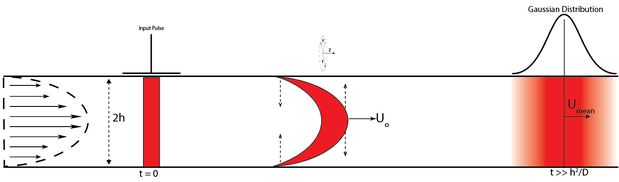
Since Taylor-Aris dispersion is a combination of laminar flow and diffusion, we are able to study their combined effect by looking at their respective constitutive equations. When only the pressure-driven flow is considered, the velocity profile looks like (in cylindrical coordinates): [math]\displaystyle{ U_{z}= U_{o}(1-r^2/h^2) }[/math], where [math]\displaystyle{ U_{z} }[/math] represents the velocity in the z-direction, [math]\displaystyle{ U_{o} }[/math] represents the maximum velocity, [math]\displaystyle{ r }[/math] and [math]\displaystyle{ h }[/math] represents, from the channel center, the radial distance of any point in the channel and the width of the channel respectively. It can be seen that the velocity is maximum at the center ([math]\displaystyle{ U_{z}= U_{o} }[/math], [math]\displaystyle{ r = 0 }[/math]) and at the boundaries ([math]\displaystyle{ r = +/- h }[/math]) it will be zero, satisfying the no-slip boundary condition. This velocity gradient stretches the thin strip into a parabola and with time. The parabolic strip elongates, increasing the distance between the apex and the base of the parabola in a linear fashion ([math]\displaystyle{ \approx U_{o}t }[/math]). Now, consider the movement of the colored species due to the concentration gradient between the stretched colored species and the clear liquid. The colored species at the apex of the parabola will move towards the boundaries of the channel and the species at the base of the parabola will diffuse towards the center of the channel (see Figure 3). Thus, we have diffusive flow in two different directions across the parabola which will smear the thin parabolic strip into a broad plug. The timescale for diffusion will be of the order [math]\displaystyle{ h^2/D }[/math] and after this time the thin strip would be a plug of thickness [math]\displaystyle{ \approx U_{o}* h^2/D }[/math]. Eventually, this plug can be considered as a sequence of multiple strips undergoing convective elongation and diffusive smearing and thereby forming a concentration band. This band would be symmetrical around a point that moves with the mean velocity of the fluid and this concentration band would resemble a Gaussian distribution (see Figure 3).
The width of the above mentioned plug can be calculated and it is [math]\displaystyle{ \sqrt{h^2} \approx\sqrt{U_{o}^2*(h^2/D)*t} }[/math]. This gives us the approximated axial diffusion coefficient for the colored strip, [math]\displaystyle{ D_{z}\approx U_{o}^2*h^2/D }[/math]. Therefore, it can be seen that the effective diffusivity of the colored strip will be [math]\displaystyle{ D^* \approx D+U_{o}^2h^2/D }[/math]. Qualitatively, one can think in the following way, when the initial colored strip is stretched, the length across which diffusion happens increases and hence an increase in diffusion. Additionally, due to the dependence of [math]\displaystyle{ D^* }[/math] on [math]\displaystyle{ D^{-1} }[/math], solutes with very low diffusivity coefficients will have a very high dispersion (refer Video 2). More importantly, in order to observe Taylor dispersion, the timescale of observation has to be much larger than the time scale of diffusion ([math]\displaystyle{ t_{p}\gt \gt h^2/D }[/math]) and at lengths much larger than [math]\displaystyle{ P_{e}h }[/math]. In both these constraints, there is a direct relationship to the channel width, and hence microfluidic domains should be a much easier place to observe Taylor dispersion.[1-5]
Video 2. Taylor dispersion of solutes with different diffusivities
Applications
Determination of Diffusion Coefficient and Hydrodynamic radii of solutes
From the above discussion, we can see that the axial dispersion is inversely related to the axial diffusivity coefficient. And the change in concentration (averaged across the channel width) of the species in the channel with respect to time is given by [math]\displaystyle{ (dC/dt) = k*(d^2C/dz^2) }[/math], where [math]\displaystyle{ k }[/math] is the dispersion coefficient.
The relation between the dispersion coefficient and the diffusion coefficient ([math]\displaystyle{ D }[/math]) is given by [math]\displaystyle{ D = r^2U_{mean}^2/48k }[/math] (this relation is only for circular channels), where [math]\displaystyle{ r }[/math] is the radius of the channel.
The diffusion coefficient carries information about how well a species can move around when there is a concentration gradient and this is clearly captured by Stokes-Einstein equation, [math]\displaystyle{ D = k_{B}T/6πηR_{h} }[/math], where [math]\displaystyle{ R_{h} }[/math] is the hydrodynamic radius of the species, [math]\displaystyle{ k_{B} }[/math] is the Boltzmann constant, [math]\displaystyle{ T }[/math] is the temperature and [math]\displaystyle{ η }[/math] is the viscosity of the liquid.
Solving the above-mentioned differential equation, we can obtain the concentration profile as a function of time and distance along the channel. And, if the concentration measurement is fixed at a point, we can obtain the time-dependent concentration profile. There are multiple solutions possible for the above-mentioned differential equation and with proper approximations (introduction of species at z=0, in an infinitesimally small region) we get
[math]\displaystyle{ C ∝ C_{o}(\sqrt{t_{o}/t})exp(U_{mean}^2(t-t_{o})^2/4kT) }[/math],
[math]\displaystyle{ t_{o}=z/U_{mean} }[/math] (residence time) and is approximately equal to the time of peak concentration in the distribution (see Figure 3). This is nothing but a time-dependent Gaussian distribution, therefore we can rewrite the above equation as
[math]\displaystyle{ C ∝ C_{o}exp-((t-t_{o})^2/2σ^2) }[/math],
where the dispersion coefficient can be obtained from the Gaussian width, [math]\displaystyle{ σ }[/math].
[math]\displaystyle{ k=U_{mean}^2σ^2/2t_{o} }[/math]. The initial approximation of introducing the solute species at an infinitesimally small region at [math]\displaystyle{ z=0 }[/math] is not practically possible therefore the concentration is observed at two different points to avoid any compensating factors that needs to be introduced to correct the initial approximation, and the dispersion coefficient is given by
[math]\displaystyle{ k= U_{mean}^2(σ_{2}^2-σ_{1}^2)/2(t_{2}-t_{1}) }[/math].
From an applications perspective, the concentration is usually measured indirectly using an UV absorbance data and this is facilitated by the Beer-Lambert law,
[math]\displaystyle{ A = εlC }[/math],
where [math]\displaystyle{ ε }[/math] is the extinction coefficient and [math]\displaystyle{ l }[/math] is the path length of the light through the sample.
Here, we can see that once we obtain the dispersion coefficient [math]\displaystyle{ k }[/math] we can determine the diffusion coefficient [math]\displaystyle{ D }[/math] and the hydrodynamic radii [math]\displaystyle{ R_{h} }[/math]. However, we have to note that we have averaged the concentration across the channel width and this puts a serious limitation on the channel diameter when we have to use this method to determine the properties of solute.[1-7]
References
1. Taylor Geoffrey Ingram. Dispersion of soluble matter in solvent flowing slowly through a tube. Proc. R. Soc. Lond.. 1953, A219186–203. DOI: 10.1098/rspa.1953.0139,
2. Taylor Geoffrey Ingram. Conditions under which dispersion of a solute in a stream of solvent can be used to measure molecular diffusion. Proc. R. Soc. Lond..1954, A225473–477. DOI: 10.1098/rspa.1954.0216,
3. Aris, R. On the Dispersion of a Solute in a Fluid Flowing through a Tube. Proc. R. Soc. London, Ser. A, 1956, 235, 67– 77, DOI: 10.1098/rspa.1956.0065.
4. Squires, Todd M. and Quake, Stephen R. Microfluidics: Fluid physics at the nanoliter scale. Reviews of Modern Physics. 2005, v77(3). DOI: 10.1103/RevModPhys.77.977
5. Alizadeh, A., Nieto de Castro, C.A. & Wakeham, W.A. The theory of the Taylor dispersion technique for liquid diffusivity measurements. Int J Thermophys .1980, 1, 243–284. DOI: 0.1007/BF00517126.
6. Philipp Lemal, Alke Petri-Fink, and Sandor Balog. Nanoparticles and Taylor Dispersion as a Linear Time-Invariant System. Analytical Chemistry, 2019, 91 (2), 1217-1221. DOI: 10.1021/acs.analchem.8b04228
7. Bird, R. et al. Transport Phenomena; John Wiley, New York,1960.
