Kam Taghizadeh Week 2

From OpenWetWare
Jump to navigationJump to search

Template

Kam Taghizadeh's Template can be Found Here

Purpose of the Week 2 Assignment

  • The purpose of this week's assignment is to utilize models to infer how to properly analyze and treat pandemics such as Covid-19.

Methods and Results

Methods

  1. Watched the The role of applied math in real-time pandemic response: How basic disease models work You Tube video and recorded two questions regarding the material.
  2. After recording two questions, I read the information on this website The SIR Model and interpreted the following questions:
    1. What happens if initial I = 0?
    2. What does it mean that the red line increases so rapidly?
    3. What does it mean that the green line also rises rapidly, but not as rapidly?
    4. What does it mean that the green line reaches nearly 1,000?
  3. Visited SIR disease modeling website Epidemix and chose the model type "Stochastic Spatial IBM" because it shows the average amount of people in each state of infection over time.
    • Took a screenshot of the original graph shown, without tampering with the parameters, and explained what it is showing.
    • Changed some of the parameters, listed below. Each change was noted along with its variation from the original graph.
    1. Edited the "Choose Control Strategy" and changed the vaccination unit from .5 to .8.
    2. Edited the "Define infection and transmission features" and changed the length of symptomatic infectious period (days) from 10 to 20 days.
    3. Edited the "Define host population features" and changed the population from 100 to 1000.
    4. Edited the "Define infection and transmission features" and changed the length of symptomatic infectious period (days) from 10 to 30 days.
    5. Edited the "Set simulation parameters" and changed number of days from 100 to 365.
    6. Edited the "Select infection states to consider" and changed the infection states to only include infectious-symptomatic and recovered.
    7. Edited the "Define spatial specific population and transmission parameters"and changed it to spatial.
    8. Edited the "Define host population features" and changed the population size to 75.
    9. Edited the "Define spatial specific population and transmission parameters" and changed the side length to 50.
    10. Edited the "Define host population features" and changed the population from closed to open.
  4. Read this article"Modelling the COVID-19 epidemic and implementation of population-wide interventions in Italy" and based on the figure 1, answered the following questions:
    1. How did the authors modify the simple SIR model to take into account features of the COVID-19 pandemic?
    2. What public health policy implications does their model have?
  5. Viewed comic on University COVID Model and noted why it is funny.
  6. Wrote scientific conclusion which included a summary of the research done for this week's assignment.

Results

  1. Questions noted regarding the The role of applied math in real-time pandemic response: How basic disease models work YouTube video.
    1. How would one be able to incorporate the rate at which a virus mutates within this type of model?
    2. How will models look if we only have partially working vaccines?
  2. Questions from The SIR Model
    1. What happens if initial I = 0?
      • If initial I=0, then that means that there are 0 people who have recovered from the virus, and 0 people who have died, since one who does not have the virus can neither get killed or recovered from it.
    2. What does it mean that the red line increases so rapidly?
      • A rapidly increasing red line means that the number of infected people is rising, as the the virus is highly contagious.
    3. What does it mean that the green line also rises rapidly, but not as rapidly?
      • The green line represents recovered people. The line rises rapidly but not as rapidly because the time it takes to get infected is a lot shorter than the time it takes to recover.
    4. What does it mean that the green line reaches nearly 1,000?
      • When the green line reaches nearly 1,000, it means that mostly all of those who were infected have recovered.
  3. Figures from Epidemix, the model type chosen is Stochastic Spatial IBM, due to its display of the average amount of people in each state of infection over time.
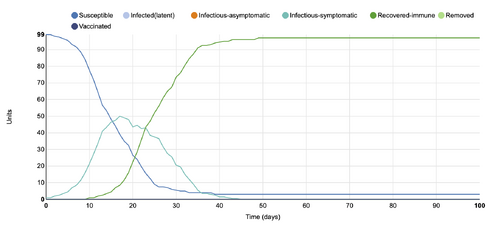
    1. Figure 1: Initial graph from the Stochastic Spatial IBM Model
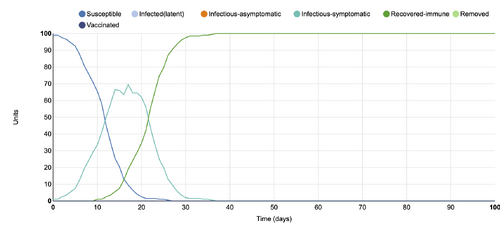
      • caption
        • This graph shows the initial conditions, without any changes in the parameters. It is displayed that susceptible cases go down as infectious-symptomatic goes up. Furthermore, recovered-immune rapidly rises as susceptible cases rapidly decline.
    2. Figure 2: Stochastic Spatial IBM Model with changed parameter within "Choose Control Strategy"
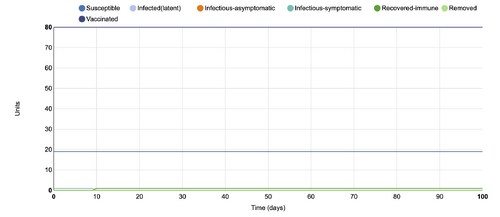
      • caption
        • This graph shows a parameter changed within the "choose control strategy" category, where the vaccination unit was changed from .5 to .8. In comparison to the initial conditions, by changing the parameters in this way, the new graph shows the susceptible line, and the infectious-symptomatic line as completely flat.
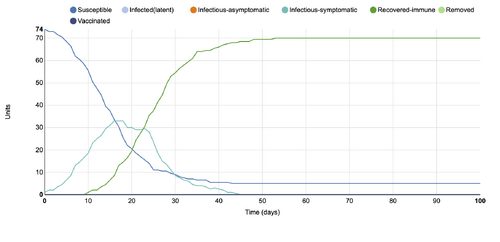
    3. Figure 3: Stochastic Spatial IBM Model with changed parameter within "Define infection and transmission features"
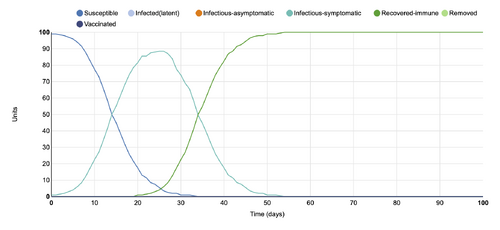
      • caption
        • This graph shows a parameter changed within the"Define infection and transmission features" category, where the length of symptomatic infectious infectious period (days) was changed from 10 to 20. When comparing to the initial conditions graph, it can be seen that the number of infectious-symptomatic people rises when the length of their infectious days increased to 20. At 20 days in the initial condition, there are around 45 infectious-symptomatic units. In the graph with changed parameters, at 20 days, there are around 83 infectious-symptomatic units.
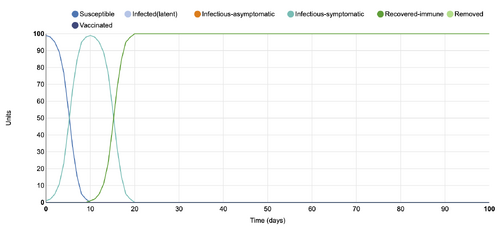
    4. Figure 4:Stochastic Spatial IBM Model with changed parameter within "Define host population features"
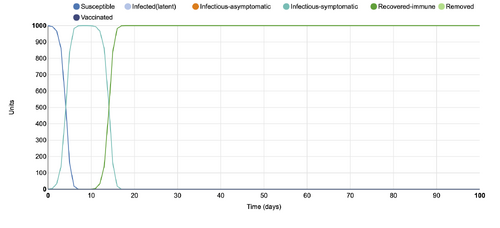
      • caption
        • This graph shows a parameter changed within the "Define host population features" category, where the population was changed from 100 to 1000. In comparison to the initial conditions graph, this graph displays many more units (up to 1000) than the 100 units that the initial graph displays. The changed parameter graph shows all 1000 units as infectious symptomatic for a period of 15 days, while the 100 unit graph shows only half of the population as infectious-symptomatic.
    5. Figure 5:Stochastic Spatial IBM Model with changed parameter within "Define infection and transmission features"
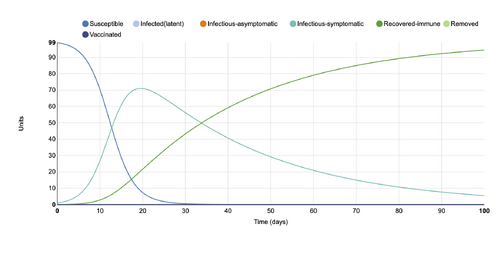
      • caption
        • This graph shows a parameter changed within the "Define infection and transmission features" category, where the length of symptomatic infectious period (days)changed from 10 to 30 days. It can be seen that the decline of infectious-symptomatic units takes a much longer time than the initial conditions graph, as well as the recovered-immune line.
    6. Figure 6:Stochastic Spatial IBM Model with changed parameter within "Set simulation parameters"
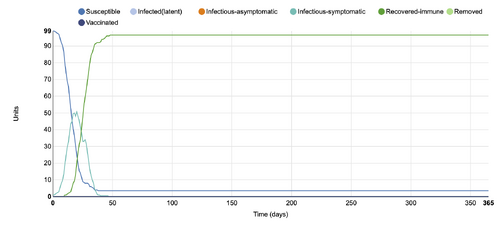
      • caption
        • This graph shows a parameter changed within the "Set simulation parameters", where the number of days was changed from 100 to 365. In comparison to the initial conditions graph, the data is more skewed to the left, due to more time being added on the x axis. The infection states remain the same however.
    7. Figure 7:Stochastic Spatial IBM Model with changed parameter within "Select infection states to consider"
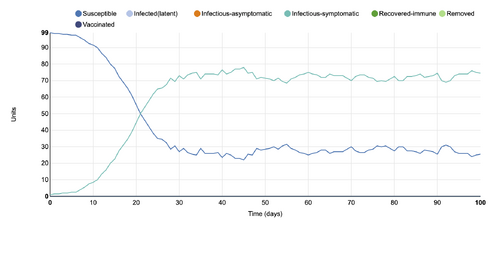
      • caption
        • This graph shows a parameter changed within the "Select infection states to consider" category, where only the infectious-symptomatic was selected to be displayed. There is a difference between what is shown for infectious-symptomatic in the initial graph and what is shown in the changed parameter graph. It appears that in the changed graph, the infectious-symptomatic seems to flatten but not decline. In the initial graph, it shows that it does decline.
    8. Figure 8:Stochastic Spatial IBM Model with changed parameter within "Define spatial specific population and transmission parameters"
      • caption
        • This graph shows a parameter changed within the "Define spatial specific population and transmission parameters" category, where the parameter was changed from clustered to spatial. It can be seen that infectious-symptomatic has increased in the changed graph.
    9. Figure 9:Stochastic Spatial IBM Model with changed parameter within "Define host population features"
      • caption
        • This graph shows a parameter changed within the "Define host population features", where the population size was changed from 100 to 75. In the graph, it can be seen that the proportions have remained the same as the initial conditions graph.
    10. Figure 10:Stochastic Spatial IBM Model with changed parameter within "Define spatial specific population and transmission parameters"
      • caption
        • This graph shows a parameter changed within the "Define spatial specific population and transmission parameters" category, where the side length was changed to 50 from 100. The data goes up to 100 units for each infection state.
    11. Figure 11:Stochastic Spatial IBM Model with changed parameter within "Define host population features"
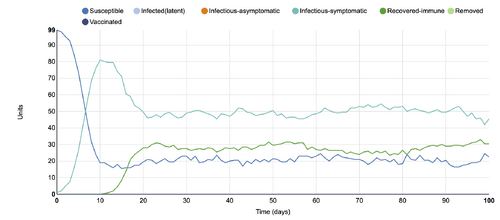
      • caption
        • This graph shows a parameter changed within the "Define host population features" category, where the population was changed from closed to open. This means that the simulation is affected by other conditions that would otherwise not be present in a closed model. So, in this graph, it can be seen that the recovered-immune line has declined greatly, and the infectious-symptomatic line has increased.
  4. Questions from the article "Modelling the COVID-19 epidemic and implementation of population-wide interventions in Italy".
    1. How did the authors modify the simple SIR model to take into account features of the COVID-19 pandemic?
      • The authors modified the simple SIR model by distinguishing between detected and undetected cases of covid-19 infection, along with severity of one's illness. SIDARTHE is the name of their model, which includes: S-susceptible,I-infected,D-diagnosed,A-ailing,R-recognized,T-threatened, H-healed, and E-extinct.
    2. What public health policy implications does their model have?
      • Their model can provide policymakers methods in which they could predict the outcome of certain circumstances. Based on these tools, they have confirmed that strict social distancing, contact tracing, and lockdown are mandatory to help slow the spread of the virus.
  5. Why is the University COVID Model so funny?
      • This model was funny because the physics major underestimated how often college students go out to party. When they're out, they increase risk of contracting the virus.

Scientific Conclusion

This week's assignment highlighted the importance of models when it comes to pandemics and epidemics. Models can provide tools to predict the outcome of various circumstances, which can be extremely crucial for making any positive step forward. The SIR model can display the rate of recovery, infection, and death, which are all important factors when navigating how to deal with a global pandemic. Therefore, it is important for government bodies to recognize the work of researchers and their models, to help society conquer this virus.

Acknowledgments

  1. Copied syntax from BIOL368/F20 Week 1 Page
  2. Copied syntax from Nathan R. Beshai
  3. Copied instructions and websites from BIOL368/F20 Week 2 Page
  4. Watched this video and wrote two questions The role of applied math in real-time pandemic response: How basic disease models work
  5. Read "The SIR Model" and answered questions regarding it
  6. Copied the Stochastic Spatial IBM model from Epidemix
  7. Worked with Taylor Makela. We collaborated through text, and discussed various parameter changes on our models.

References

  1. OpenWetWare. (2020). BIOL368/F20:Week 1. Retrieved September 16, 2020, from https://openwetware.org/wiki/BIOL368/F20:Week_1
  2. OpenWetWare. (2020). BIOL368/F20:Week 2. Retrieved September 16, 2020, from https://openwetware.org/wiki/BIOL368/F20:Week_2
  3. Fefferman, N. (2020, April 1). The role of applied math in real-time pandemic response: How basic disease models work. [Youtube Video]. NIMBioS. Retrieved from https://www.youtube.com/watch?v=Ewuo_2pzNNw&feature=youtu.be.
  4. Epi-Interactive. (n.d). Epidemix Version 2. Retrieved September 16, 2020, from https://www.epidemix.app/#.
  5. Giordano, G., Et. Al. (2020). Modelling the COVID-19 epidemic and implementation of population-wide interventions in Italy. Nature Medicine, 30,855-860. https://doi.org/10.1038/s41591-020-0883-7.
Retrieved from "https://openwetware.org/mediawiki/index.php?title=Kam_Taghizadeh_Week_2&oldid=1089345"