IGEM:IMPERIAL/2006/project/Oscillator/Theoretical Analyses/3Dto2D

From OpenWetWare
Jump to navigationJump to search

Analysis of the Model of the Molecular Predation Oscillator


Model Simplification



  • Why we can simplify the 3d Model into a 2D Model
  • Simplification is possible because of the similarity of the growth rates of the predator terms (V and W) in the 3D Model
  • Their complex production terms are identical
  • Only their dissipative terms (-d1*V and -d2*W ) varies
  • A simple hypotheses could lead to a very big simplification in our analysis
  • A 2D analysis is much simpler, and still will give us valid prediction on whether the system will oscillate.



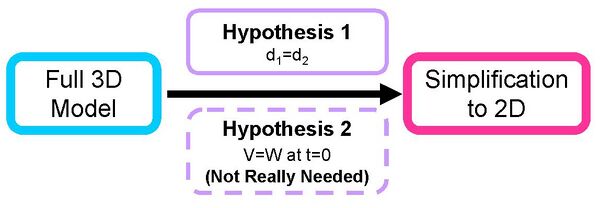
  • Required Hypotheses for Simplification
  • Hypothesis 1: to ensure V and W have same growth rates
  • Hypothesis 1: d1=d2)
  • Hypothesis 2:To have equality of the initial conditions
  • Hypothesis 2: [aiiA] = [LuxR] at time t=0
  • Under previous 2 Hypotheses
  • aiiA and LuxR start at the same concentration
  • they have the same rate of production and degradation
  • hence they have at the same concentration throughout
  • System then can be simplified to



Summary of our approach


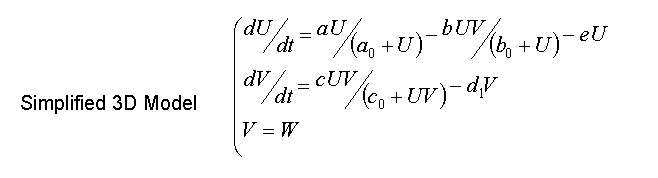
  • Validity of the hypotheses
  • Hypothesis 1 : d1=d2
  • The assumption of d1=d2 is feasible because aiiA and LuxR within the cells will be washed out at the same rate in chemostat.
  • As long as we can ensure the washing out rate is much more dominant than their natural half-life (easily achieved) the assumption should hold
  • Hypothesis 2 is not really essential
  • it is fortunate as it was hard to ensure
  • if d1=d2, the difference between W and V will decay to 0 exponentially (with a time constant 1/d1)
  • therefore after a little time we can assume V=W
  • the larger d1, the faster the assumption becomes valid
  • the larger the difference between initial values of V & W, the longer the settling time of reaching V=W only
  • In particular we are sure that the condition on the parameters for obtaining a limit cycle will still be identical in 2D and 3D despite of the initial concentrations of U V W.



  • Problem : in Theory , there is a Huge Difference Between 2D and 3D
  • Poincare-Bendixson Theorem works for 1D and 2D only, but not 3D
  • We only need simple requirements for a limit cycle in 2D
  • In 3D the requirement is more complex - or much more complex
  • So are our results in 2D worth anything ?
  • If our hypotheses are exactly met: Yes!
  • In practice hypotheses not exactly met, but we have a margin of error
  • A slight error on Hypothesis 2 is not important
  • Slight error on hypothesis 1 (d1 not strictly equal to d2): 2 Scenarii
  • Scenario 1: (the kind one)
  • For d1=d2 and a range of parameters well chosen we have oscillations
  • Because the system is well behaved , we still have oscillations at the vicinity of these parameters (hence for d1 slightly different from d2)
  • Scenario 2: (the not so nice one)
  • [aiiA] and [LuxR] get more and more out of synchronisation
  • However, if the hypotheses are almost met, we can hope to have a few synchronised cycles



  • Conclusion
  • There is a lot to learn from the 2D model
  • A word of caution:
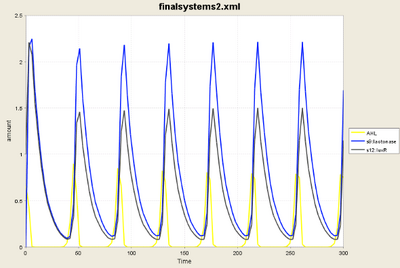
Simulation of Full 3D model done by Cell Designer


  • The simulation above shows individual cycles of [aiiA] and [LuxR]
    • Frequencies are equal
    • Profiles very similar
    • Peak amplitudes different
    • Clearly for such cycles d1=d2 was not met and yet we have oscillations. We therefore have to study the 3D case in its entirety at some point
  • However for our current interest of whether the system can result in generation, 2D case of d1=d2 should be enough


<html> <script type="text/javascript" language="javascript"> var sc_project=1999441; var sc_invisible=1; var sc_partition=18; var sc_security="18996820"; </script>

<script type="text/javascript" language="javascript" src="http://www.statcounter.com/counter/frames.js"></script><noscript><a href="http://www.statcounter.com/" target="_blank"><img src="http://c19.statcounter.com/counter.php?sc_project=1999441&java=0&security=18996820&invisible=1" alt="website statistics" border="0"></a> </noscript> </html>

Retrieved from "https://openwetware.org/mediawiki/index.php?title=IGEM:IMPERIAL/2006/project/Oscillator/Theoretical_Analyses/3Dto2D&oldid=84422"