Holcombe:CircularStatistics
Recent members• Alex Holcombe
|
Projects• Testing Booth Calendar |
|
Technical• Skills Checklist |
Other• Plots,Graphs
|
Data is sometimes circular, like angles for direction selectivity and orientation selectivity. Most scientists are familiar with the normal distribution, and its standard deviation (σ) is used frequently to quantify the spread of a distribution. Sometimes we would like to compare a distribution on a circular variable to one on a non-circular variable. In our case people report the position of a blob revolving periodically about fixation. Histogram of the data shows the distribution of times corresponding to positions reported. We would like to estimate the standard deviation of the process that yields the variability in time. For instance there may be variability in when the observer samples the position, perhaps following a normal distribution. This would be non-circular mechanism whose results end up wrapped into circular form in our data.
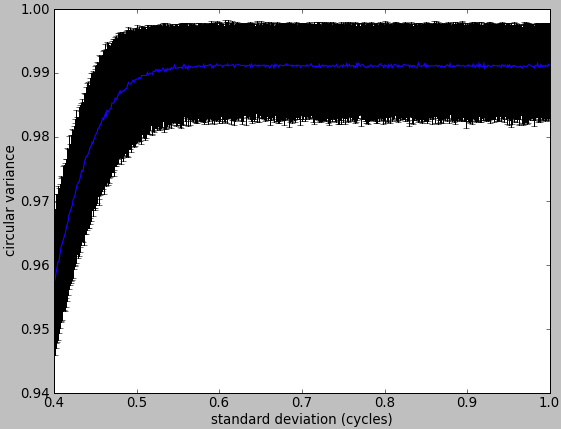
For each linear std dev, drew a sample of 10,000 numbers, wrapped it, then calculated the circular variance. Repeated 1,000 times to construct histogram from which got 90% confidence interval.
 It is apparently nearly impossible to distinguish among values greater than about .45 of a cycle (162 deg). If we zoom in on this part of the top left graph, we see the curve nearly completely level off, and even with 10,000 samples the confidence intervals are much bigger than the change of circular variance from .5 to 1 std dev.
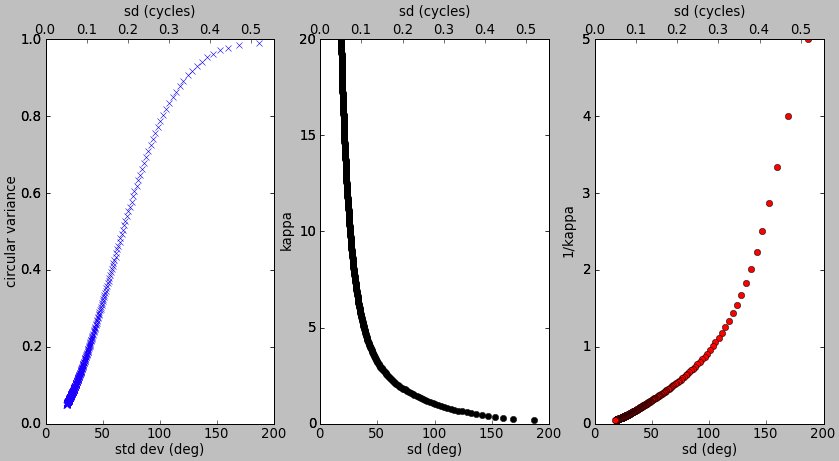
When reporting the equivalent std dev, our CI should reflect the 'conversion uncertainty' in going from circvar to std dev. This would require checking on the below graph the smallest std dev that could yield that circvar. And that depends on the sample size of the simulation that yielded the below graph, which is arbitrary. Hopefully the CI on the circvar (which R calculates with simple bootstrapping) is so large that it swamps the 'conversion uncertainty'
It is apparently nearly impossible to distinguish among values greater than about .45 of a cycle (162 deg). If we zoom in on this part of the top left graph, we see the curve nearly completely level off, and even with 10,000 samples the confidence intervals are much bigger than the change of circular variance from .5 to 1 std dev.
When reporting the equivalent std dev, our CI should reflect the 'conversion uncertainty' in going from circvar to std dev. This would require checking on the below graph the smallest std dev that could yield that circvar. And that depends on the sample size of the simulation that yielded the below graph, which is arbitrary. Hopefully the CI on the circvar (which R calculates with simple bootstrapping) is so large that it swamps the 'conversion uncertainty'