BME100 s2017:Group6 W8AM L3

BME 100 Spring 2017	Home People Lab Write-Up 1 | Lab Write-Up 2 | Lab Write-Up 3 Lab Write-Up 4 | Lab Write-Up 5 | Lab Write-Up 6 Course Logistics For Instructors Photos Wiki Editing Help
OUR TEAM Name: Madison Brandt Name: Hannah Griffin Name: Yvonna Chan LAB 3 WRITE-UP Descriptive Stats and Graph When finding results for the average heart rate and temperature for both Gold Standard and Spree, we found that there was a significant difference in temperature recording between the two. However, heart rate was very similar in recording data. The average temperature for Gold Standard was 96.6 degrees Fahrenheit whereas the average temperature for Spree was 95.5 degrees Fahrenheit. There was also a difference for the results of standard deviation. The standard deviation finding was 1.92 where the standard deviation for Spree was 0.87. When finding heart rate measurements, we found that the average for Gold Standard was 98.1 bpm and 98.9 bpm was the average for Spree. For standard deviation, we found that Gold Standard's standard deviation was 23.03 whereas Spree's standard deviation was 24.88. From our findings, we can conclude that the Gold Standard did a much better job at measuring temperature externally compared to Spree. On the contrary, they both measured heart rate similarly and are both relatively accurate. In the graph of Gold Standard versus Spree for the temperature, Pearson's correlation determined that r = 0.193, which suggests a weak positive linear relationship. In the graph of Gold Standard versus Spree for the heart rate, Pearson's correlation determined that r = 0.691, which suggests a moderate positive linear relationship. 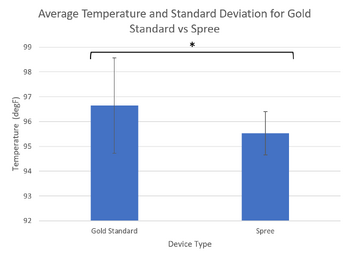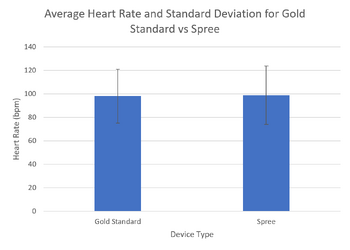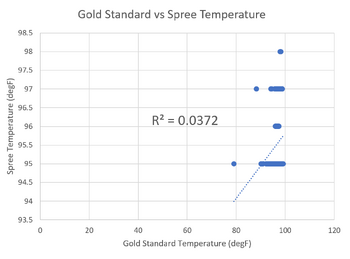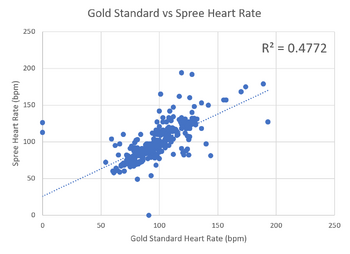Inferential Stats In order to test for statistical significance we ran a dependent (paired) t-test. We did this because we had one group of students that were tested in two different ways. Upon performing the t-test on the heart rate statistics between the gold standard using a pulse oximeter and the Spree Band, we found a p-value of 0.427. Upon performing the t-test on the body temperature statistics between the Gold Standard using the oral thermometer and the Spree Band, we found a p-value of 1.097*10^(-21). A p-test value of less than .05 shows a statistically significant difference. Since the p-test value for the temperature was far below this value, it is highly likely that the Spree Band does not give an accurate readout of body temperature. Design Flaws and Recommendations A major flaw in Spree Sports device is the temperature aspect. Compared to other devices, it is unreliable in the sense that it does not provide a constant reading and that it is not always accurate. Ways to improve this aspect of the device include: figure out the best places on the body to measure temperature; use one of these spots for the device to measure or to completely disregard the temperature aspect of the device. Although it is a good aspect to have on a device like this, finding body temperature is done best when found internally instead of externally. However, if they were to continue the temperature readings, it would be best to look into more high tech temperature sensors to use for the device. Experimental Design of Own Device In order to test the accuracy and validity of our device, we have decided to design an experiment that compares our pressure sensor insole to a highly accurate force plate device, such as the AMTI AccuGait Walkway. This device is designed to read the pressure distribution of a person's feet as they walk over it in order to give feedback on gait. This is essentially the same function of our device. To compare our device to the gold standard, we will have subjects walk with our insole in their shoes and gather the data. We will then have the same subject walk across the force plate, and gather the data from that. After that, we will analyze the readouts of both devices and compare force on various specified points of the foot. We will then perform statistical analysis and find standard deviation for the various points of the foot we have chosen, comparing the gold standard to our device. In order to control the experiment, we will only change the device the patients are walking on, and keep all other variable's the same (including clothing of the patient, and time of tests in case of weight fluctuation). To randomize the experiment, we will use a variety of subjects, ranging in age, weight, and body type. To repeat the testing, we will have a multitude of subjects, as well as have each subject tested multiple times.