BME100 f2017:Group9 W0800 L3
| Home People Lab Write-Up 1 | Lab Write-Up 2 | Lab Write-Up 3 Lab Write-Up 4 | Lab Write-Up 5 | Lab Write-Up 6 Course Logistics For Instructors Photos Wiki Editing Help | |||||||
|
OUR TEAM
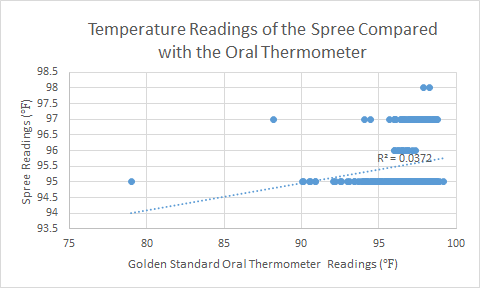
LAB 3 WRITE-UPDescriptive Stats and GraphTemperature Readings:
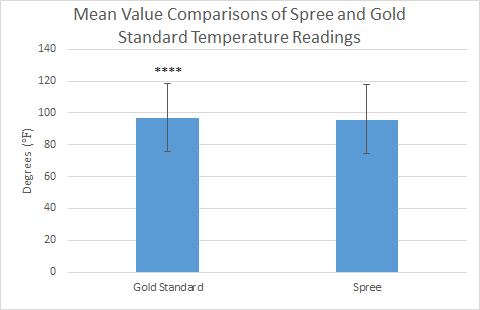
Inferential StatsThe t-test is the inferential statistical test that is appropriate for this lab because we only compare two groups to each other, not multiple groups. If there were multiple groups being compared together and not just the oral thermometer to the Spree headband and the pulse ox to the Spree headband, then an ANOVA or analysis of variance test would be required. t-test p-value produced for temperature readings of the Spree headband versus the oral thermometer gold standard: 1.09676E-21 ****
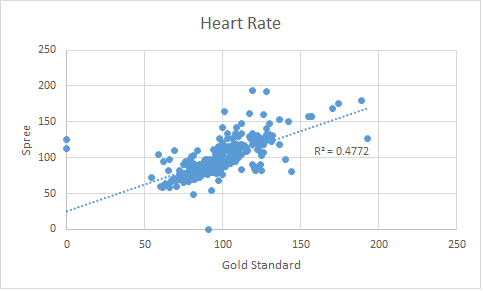
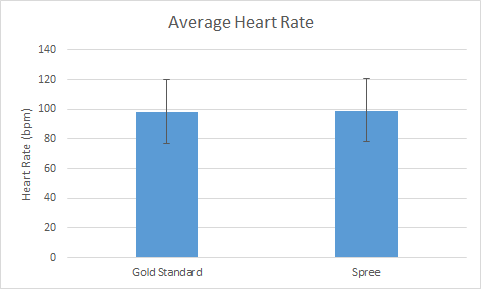
Design Flaws and RecommendationsWhile when just examining the data through comparisons of the mean values, the temperature readings of the gold standard of the oral thermometer versus the Spree headband seem to be equal, as would be desirable in deciding the effectiveness of the prototype. The Pearson’s R coefficient of correlation is also calculated as 0.19287, and this can be interpreted as the strength of correlation being small, which means that the direct correlation between the gold standard temperature reading values and the Spree headband temperature reading values exists, but is weak. The t-test value also was calculated as 1.097E-21, and the t-test produces a p value, which if less than 0.05, indicates a significant difference between the two groups. Since the p-value calculated by the t-test between the gold standard and Spree headband is incredibly small and way less than 0.05, this indicates that the temperatures read for the two devices is statistically significantly different. This shows that the Spree headband is not an effective device for measuring body temperature properly, and needs more technical testing and work to be accurate enough for market sale. Based on the raw data from the testing, part of the issue is that the Spree headband does not read decimal points, only whole numbers, and as a result, lacks the precision demonstrated in the gold standard oral thermometer. A recommendation would be to make the Spree headband more precise in its measurements, so as to match the accuracy of measurements in the gold standard. Given the data presented to compare the gold standard of the pulse ox and the Spree headband, they look very similar. The averages of the two are extremely close with its difference being less than one. The Pearson's R coefficient was calculated to be .690806 which indicates a relatively strong correlation. This proves that the spree can be considered to be used, although is not entirely accurate enough to be a complete replacement. The t-test value was calculated to be 0.427116 which shows that the data were not significantly different since it was greater than 0.05. The data was actually extremely close if looking at the scatter plot, there were only a few outliers. This could be contributed by human error or device error.
Experimental Design of Own DeviceTo test the effectiveness of the auto-injector in its ability to successfully inject liquid into tissue, the experiment will involve using a colored liquid, an intramuscular injection pad connected to a receptacle for liquid collection, and a normal syringe used in vaccinations. The reason for this is to compare the effectiveness of the auto-injector in injecting liquid with the effectiveness of the gold standard with injecting liquid, which is a normal syringe and needle traditionally used for vaccination. The specific comparison is the mass of the liquid that comes out of the needle and into the “muscle,” as this is what would be dispersed into the body in vaccinations, which will be shown by taking the mass of the liquid collected post-injection and analyzing whether they are different or not between the prototype and the gold standard.
The experimental design would involve two groups, one group where the injection of colored liquid into an intramuscular injection pad connected to a liquid collector would be performed by the auto-injector, and another group where the injection of the liquid would be performed by a normal syringe with a needle typically used for vaccination. Each group would perform 100 runs of the experiment. One run of the experiment would consist of measuring out the colored water at 0.5 mL (which will have its mass measured out beforehand), transferring that into the container for liquids in the autoinjector or into the syringe for the gold standard. The run would then include the actual injection of the colored water into the intramuscular injection pad that is connected to the container for the liquid, whether done by the auto-injector or the normal syringe. The next step would be to take the mass of the liquid that has been collected using a scale with high precision, not including the mass of the container itself. The last step would be to record the mass of the liquid for the group the run is for, and to later analyze the data.
In order to analyze the data collected from each group, there are multiple statistical analyses that need to be performed. First, the descriptive analysis of the data collected between our device and the current gold standard would be done by calculating the mean value of the mass of the liquid collected in the container after injection from the group using the gold standard syringe versus the group using the auto-injector. Standard deviation would also be calculated for in both groups to determine the variability and consistency of the masses for both the auto-injector and the gold standard syringe. A bar graph of mean values with error bars and a linear plot to determine the Pearson’s correlation coefficient of “r” would also be created to further visually analyze the data. Then, inferential analysis of the data must be performed in order to actually determine the relationship between the data found in both groups. This can be done through the use of a t-test, as there are only two groups of data to be compared. The product of the t-test would be a p-value. If the p-value is less than or equal to 0.05, then the groups’ data is statistically significant, which means that the mass of the liquid collected between the two groups is statistically different. This would indicate that the prototype is injecting a different dosage into the intramuscular injection pad than what the golden standard would inject, and as a result, the device is ineffective and would not be able to be sold without more time spent on editing the prototype, fixing it until the data in this experiment, when re-run, is comparable to the gold standard. However, if the p-value is greater than 0.05, then the groups’ data is not statistically significant, which means that the mass of the liquid collected post-injection between the two groups is statistically about the same. This would mean that our prototype is comparable to the gold standard, and effective in terms of injecting the right amount of liquid into the “muscle.”
| |||||||