BME100 f2017:Group8 W0800 L3

BME 100 Fall 2017	Home People Lab Write-Up 1 | Lab Write-Up 2 | Lab Write-Up 3 Lab Write-Up 4 | Lab Write-Up 5 | Lab Write-Up 6 Course Logistics For Instructors Photos Wiki Editing Help
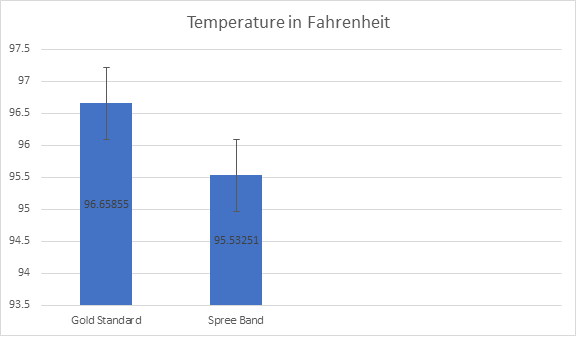
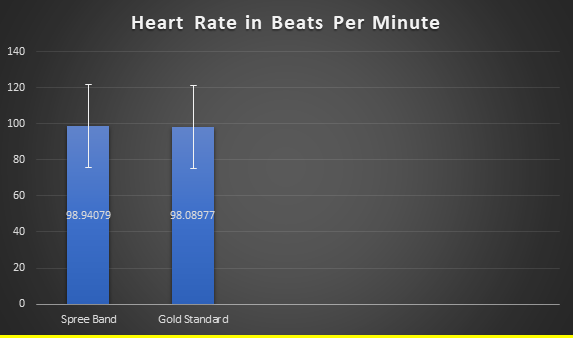
OUR TEAM Name: Chandler Ryder Name: Jinpyo Seo Name: Megan Pitts Name: Janet Vargas Name: Cassie Riggs Lab 3: Device Validation Descriptive Statistics and Graphs Mean for Temperature Gold Standard: 96.65855 Degrees Fahrenheit Spree Band: 95.53251 Degrees Fahrenheit Standard Deviation for Temperature Gold Standard: 1.918463 Degrees Fahrenheit Spree Band: 0.870378 Degrees Fahrenheit Mean for Heart Rate Gold Standard: 98.08977 Beats Per Minute Spree Band: 98.94079 Beats Per Minute Standard Deviation for Heart Rate Gold Standard: 23.03053 Beats Per Minute Spree Band: 24.83749 Beats Per Minute 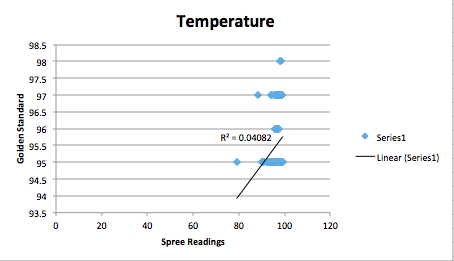Inferential Statistics and Graphs Temperature Pearson’s r: .202039 r2=0.04082 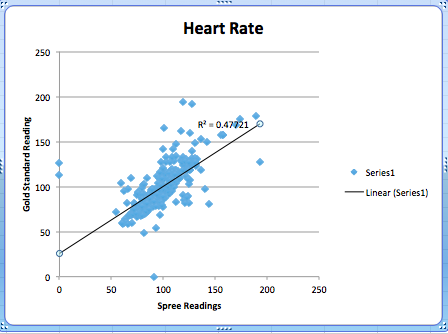Heart Rate Pearson’s r: .690806 r2=0.47721 T-test Results P-value for paired t-test for Heart Rate = 0.4271169 P-value for paired t-test for Temperature = 7.88715E-22 or essentially 0. Summary of Results Hypotheses Ho=The temperature of gold standard=The temperature measured from the device Ha=The temperature of gold standard=/=The temperature measured from the device Ho=The heart rate of gold standard=The heart rate measured from the device Ha=The heart rate of gold standard=/=The heart rate measured from the device Conclusions According to the p-values and the alpha (=0.05) from the paired t-tests… We reject the null hypothesis for temperature because the p-value of 7.88715E-22 or essentially 0 is less than=0.05, this indicates that there is evidence that the device can measure temperature well. We fail to reject the null hypothesis for heart rate because the p-value of 0.4271169 is greater than=0.05, this indicates that there is not enough evidence to prove that the device can measure heart rate well. Experimental Design of our own Device Our device is meant to help get prevent cavities, control salivary pH levels, and increase saliva production. To measure this data, we can do an unpaired t-test (=0.05) by gathering two groups of people (all in their twenties), control and experimental. The null hypothesis is that the saliva flow rate of control=saliva flow rate of experimental and the second null hypothesis is that the average number of cavities found in control=average number of cavities found in experimental. The alternative hypothesis is that saliva flow rate of control is less than the saliva flow rate of the control group and that the average number of cavities from control is less than the average number of cavities from the experimental group. Approximately 100 similar subjects will be gathered through a simple random sample. The control group will receive a placebo and the experimental will receive the gum. Our trial will occur in a time period of 6 months where the subjects will consume the gum every day after lunch. At the end of the 6-month trial, the subjects will attend a dental appointment at which the average number of cavities will be noted and the saliva flow rate with a saliva test. We can conclude whether to reject or fail to reject the claim according to the data retrieved. Control Group: the group who received the placebo Independent Variable: whether the group received the treatment or not Dependent Variable: the amount of saliva produced and the amount of cavities in each group of the experiment