BME100 f2017:Group7 W1030 L3
| Home People Lab Write-Up 1 | Lab Write-Up 2 | Lab Write-Up 3 Lab Write-Up 4 | Lab Write-Up 5 | Lab Write-Up 6 Course Logistics For Instructors Photos Wiki Editing Help | ||||||
|
OUR TEAMOUR TEAM
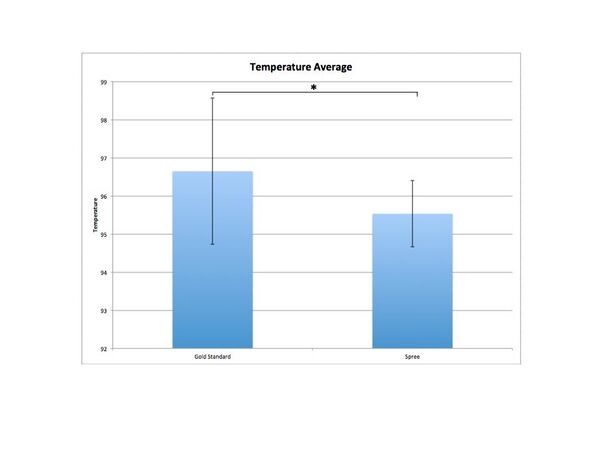
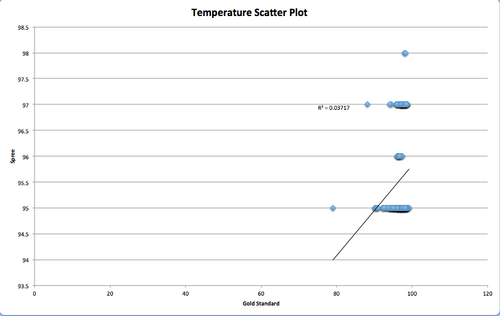
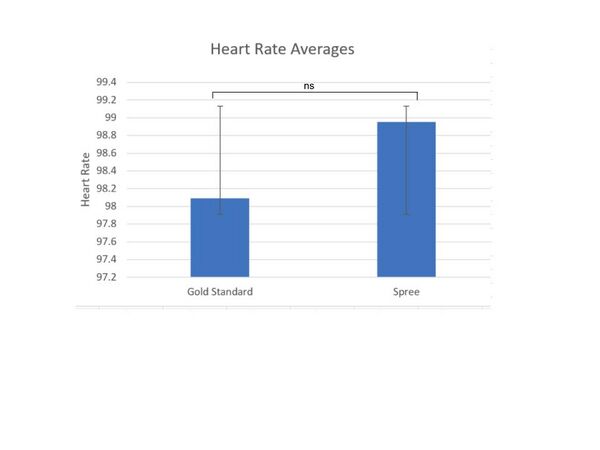
LAB 3 WRITE-UPDescriptive StatsTemperatureWe found the average/mean of gold standard data was 96.64716049 and the standard deviation was 1.922602071. We also found the average/mean of spree was 95.5308642 and the standard deviation was 0.870378299. Heart RateWe found the average/mean of gold standard data was 98.08976898and the standard deviation was 23.03054395. We also found the average/mean of spree was 98.95379538 and the standard deviation was 24.87753802. Inferential StatsTemperature AverageTemperature Scatter PlotTemperature Data DiscussionThe t-test value for temperature was 1.09676E-21. The Pearson's Correlation r value was 0.03717. Therefore, the differences between the data from the golden standard and spree are statistically significant. Though the t-test is lower than 0.05, indicating there is a less than 5% chance that if we ran the experiment again we wouldn't get the same results, the r value was significantly lower than 1. This indicates that the data are not strongly correlated. Heart Rate AverageHeart Rate Scatter PlotHeart Rate Data DiscussionThe t-test value for heart rate was 0.4271161925. The Pearson's Correlation r value was 0.4772. Therefore, the differences between the data from the golden standard and spree are not statistically significant. The t-test value is much higher than 0.05, which indicates there is a high chance that if we ran the experiment again we wouldn't get the same results. The r value was lower than 1, but in this case at least it was higher than the r value found for the temperature data. This indicates that the data are not strongly correlated to the golden standard, but are better correlated with heart rate than with temperature. Design Flaws and RecommendationsBased on these data, we conclude the spree device is ineffective at measuring one’s heart rate and temperature. We also conclude that the testing had many design and experimental flaws. One of the design flaws is that the device can move around fairly easily on the head while in use. A possible solution is an adjustable strap to keep the device from moving around (preventing incorrect measurements). Researchers could also consistently check the head placement. An experimental data flaw is the sample size. The experiment would benefit from a much wider sample of participants. Also, the heart rates and the temperature did not vary enough to accurately measure spree versus the gold standard. Measuring a wider range of body temperatures and heart rates would enable a stronger data analysis. Experimental Design of Own DeviceTo test our product’s efficacy compared to current atherectomy devices we would run an angiogram on willing volunteers. An angiogram is a diagnostic technique that uses X-rays to determine blockage in the arteries. An angiogram is capable of detecting blockages by using X-rays that are scanned after iodine contrast dye is injected. First, we would run angiograms on a large sample size of patients (ideally n>100) to measure initial arterial blockage. This sample size would need to accurately represent the demographics of populations at varying levels of risk for post-atherectomy restenosis and/or coronary artery disease. We might have multiple testing groups, such as low-risk for restenosis, medium-risk, and high-risk to evaluate efficacy at differing degrees of disease severity. Then, we would perform our atherectomy treatment. Once this is done, we would perform angiograms on the patients at three different time periods (one hour post-surgery, one month post-surgery, and one-year post surgery). This would enable us to test efficacy over different time scales. To compare against the gold standard of the best atherectomy treatment on the market, we would compare our data to data already collected on the gold standard. Likely though, we would need to perform the same experiment with the same sample size, group variations, and population representation using the gold standard device and use this data for comparison. We would need to find the mean and standard deviation within both the new device test groups and the gold standard groups (and between groups in each), as well as perform a t-test and Pearson's r correlation (to determine statistical significance). | ||||||