BME100 f2017:Group6 W0800 L3

BME 100 Fall 2017	Home People Lab Write-Up 1 | Lab Write-Up 2 | Lab Write-Up 3 Lab Write-Up 4 | Lab Write-Up 5 | Lab Write-Up 6 Course Logistics For Instructors Photos Wiki Editing Help
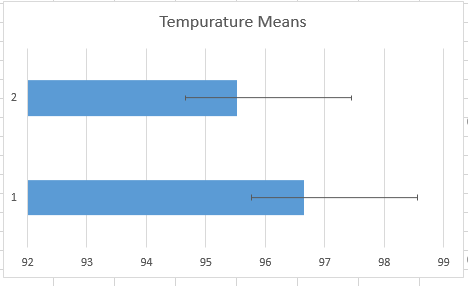
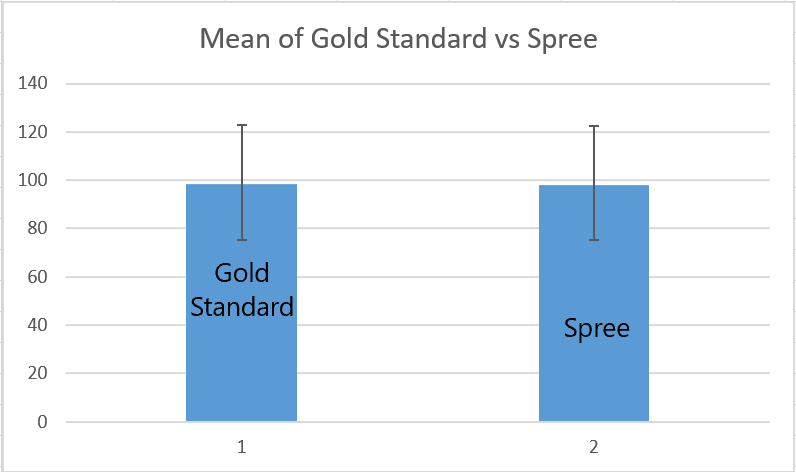
OUR TEAM Name: Your name Name: Your name Name: Your name Name: Your name Name: Your name Name: Your name LAB 3 WRITE-UP Descriptive Stats and Graph After analyzing the temperature data, through graphing and finding means for the gold standard and the spree collection, we found that the difference between the two was significantly different. The mean of the Gold Standard was 96.64 degrees while the mean of the Spree was 95.53 degrees. The standard deviation of the Gold Standard data set was 1.9 degrees and the standard deviation of the Spree data set was significantly lower at 0.9 degrees. The heartrate data showed very positive results for the Spree band because the data set from the Spree hat was very similar to the Gold Standard. The mean of the data for the Spree hat was 98.1 and the mean for the Gold Standard was 98.2. In addition to this the standard deviation of the Spree hat was smaller than the standard deviation of the Gold Standard: 23.0 and 24.5. When we ran a Pearsons r correlation analysis on the data we discovered that the Spree and Gold Standard held a positive correlation of 0.691 which means that the Spree band was fairly accurate at measuring the heartrate of the user. 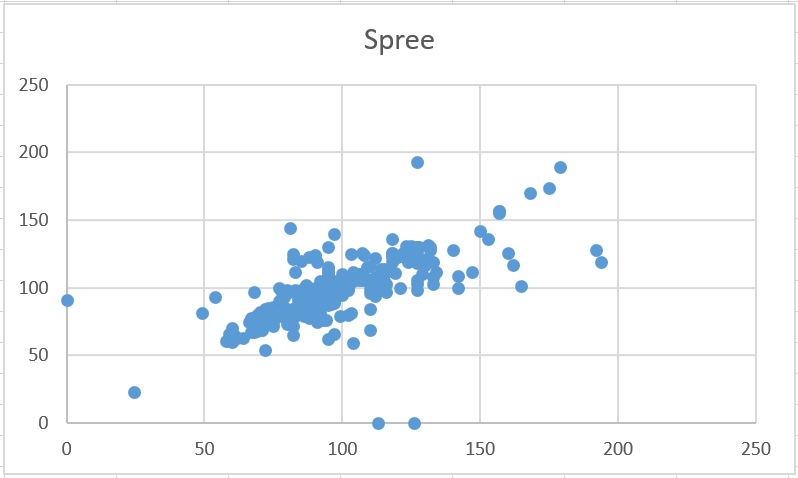Inferential Stats p value for Student's two-tailed, paired t-test for Heartrate: 0.427 r value for heartrate: 0.691 This p value is greater than 0.05. From this we can infer that the difference between the two sets of data is not significant. This is what we want in this case, because we want the Spree readings for heartrate to be as close as possible to the gold standard readings. From this p value we can infer that the Spree band does a relatively good job of measuring heartrate. The r value further confirms this. The correlation is not perfectly linear, however, it is fairly close. 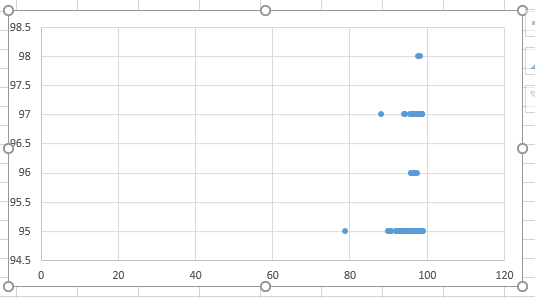p value for Student's t-test for Tempurature: 1.09E-21 r value for temperature: 0.01979 This p value indicates that the difference between the two sets of data for temperature is extremely significant. The p value is far smaller than the accepted standard of 0.05. From this we can infer that the Spree band does not do a good job at taking temperature readings. The r value further confirms this because the correlation is practically zero. Design Flaws and Recommendations Our p-value for temperature was significantly less than 0.05. Meaning, the head band is not a viable resource to detect temperature. Thus, there is no correlation between the spree head band and the gold standard. This was possibly due to the fact that taking temperature from the head area is very difficult because the forehead is exposed to environmental factors that can play a role in throwing off the temperature reading. By taking a temperature orally, you mitigate the environmental factors that can throw off the temperature reading. It is also a possibility that the subjects could have also possibly tinkered with the device which may have caused some off-readings. They should have monitored the subjects closer to prevent this from happening. Another flaw noted was that for some spree values there was no gold standard and vice versa for both temperature and heart rate. This is just a good reminder to include all data when running a scientific test. Also, there were a few cases where the spree showed a measurement of zero. This shows an error in the data because there is no way to have a temperature or heart rate of zero. Experimental Design of Own Device Our device uses UV light to sanitize hands. The prototype is a hollow box that has two circular holes to place your hands within. Your hands are then exposed to the bacteria killing UV lights which are situated along the insides of the box. Our claim is that the advantage of using this device is that it is quicker and more efficient than taking the time to wash your hands with soap and water. Our experiment must prove whether or not the device can produce the same cleanliness as washing one’s hands, and whether or not it can produce this cleanliness with only 10 seconds of exposure to the light source. There will be 5 groups of subjects: the control group and 4 experimental groups. Each experimental group will be exposed to the UV light for a different amount of time: 5 seconds, 10 seconds, 15 seconds, or 20 seconds. Each group should have 100 people. All subjects will be asked to not wash their hands or use any type of sanitizing product two hours prior to the experiment. Additionally, each subject will be asked prior to the experiment to run their hands along a variety of objects such as door knobs and countertops. This will ensure that all test subjects acquire about the same amount of bacteria before the cleansing occurs. The control group will then wash their hands, as they regularly do, using standard liquid soap and water. The experimental groups will cleanse by placing their hands under the UV light for the allotted times of 5, 10, 15, or 20 seconds. The cleanliness of the subjects’ hands can then be measured using a method called rapid hygiene monitoring. This method utilizes ATP bioluminescence technology. ATP is a molecule found in all living cells, so it is an accurate way of measuring the amount of bacteria on your hand. If you have more bacteria, there is more ATP. When ATP is combined with the enzyme luciferase, a reaction takes place which produces light. The amount of light produced can be measured using a luminometer with units expressed in candela. The greater the value for luminous intensity, the more ATP present, thus the more bacteria on your hand. Now we have numerical data for the average cleanliness of the control group and each experimental group. The next step is for us to determine if this difference in averages is statistically significant. To do this we perform an ANOVA test. From this test we can finally answer the question “Does our device cleanse as effectively as the traditional method of washing hands?” and if so “What is the smallest time interval under the UV light that is still effective at sanitizing hands?”