BME100 f2017:Group5 W1030 L3
| Home People Lab Write-Up 1 | Lab Write-Up 2 | Lab Write-Up 3 Lab Write-Up 4 | Lab Write-Up 5 | Lab Write-Up 6 Course Logistics For Instructors Photos Wiki Editing Help | ||||||
|
OUR TEAMLAB 3 WRITE-UPDescriptive Statistics and Graphs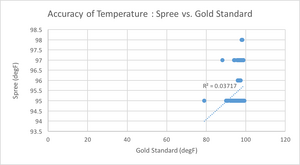 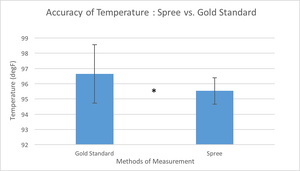 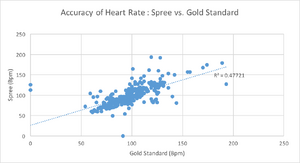 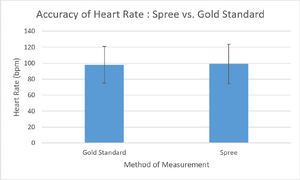 HEART RATE TEMPERATURE Inferential StatisticsA t-test was performed for each biometric category because within Heart Rate and Temperature, respectively, there were two data sets being compared: the Gold Standard and the Spree.
Since t-tests are used for 2 data sets, the t-test was used as opposed to the ANOVA, which is for more than 2 data sets.
The t-tests were both 2 tailed (because we did not predict which data set would be bigger/smaller/etc) and paired (because the same people were used for both data sets in each Temperature and Pulse test)
The p-value was determined using Excel: HEART RATE The p-value of the heart rate, being much larger than 0.05, indicates that the difference between the two data sets (Gold Standard and Spree) is NOT significant. That is, the Spree is a relatively accurate (as it is comparatively close to the Gold Standard), for measuring heart rate. The p-value of the temperature, being much smaller than 0.05, indicates that the difference between the two data sets (Gold Standard and Spree) IS significant. This was demonstrated above in the temperature bar graph with a star. This means that the Spree is not accurate when it comes to measuring human body temperature, when compared to the gold standard.
Design Flaws and RecommendationsThe design flaws of this device are largely concerning its accuracy when it comes to measuring body temperature (see Inferential Statistics section). This may be due to the fact that it is an external device, thus making it harder to accurately measure body temperature (which is more constant and warmer on the inside of the body). The creators of the device should probably reevaluate how they measure body temperature as it is difficult to measure with a hat. In addition, the fact that the measurements are rounded to the nearest whole number, whereas the Gold Standard measurements were rounded to the nearest tenth, would definitely have impacted the accuracy of the readings by introducing more rounding error, and thus more discrepancy between the Spree and the Gold Standard measurements.
Experimental Design of Own DeviceFor our experiment, the UV sensor we will create will have to be compared to another UV sensor that has been proven to be accurate. We would have multiple trials testing the tattoo against the independent variable, sunscreen. The dependent variable would be the time it took for the tattoo to change color. These trials would use random groups to avoid adding bias to the experiments. We would use a two-tailed t-test to compare the time it takes for the tattoo to change color with sunscreen on it and without sunscreen on it. If the t-test shows that there is a significant difference (<.05) in time to change color, then it means that our tattoo is taking longer to change colors because of the sunscreen and without the sunscreen it changes colors much faster. This data would show that our tattoo is only changing colors when the UV rays are able to hit the tattoo. | ||||||