BME100 f2017:Group15 W1030 L3
| Home People Lab Write-Up 1 | Lab Write-Up 2 | Lab Write-Up 3 Lab Write-Up 4 | Lab Write-Up 5 | Lab Write-Up 6 Course Logistics For Instructors Photos Wiki Editing Help | ||||||
|
OUR TEAM
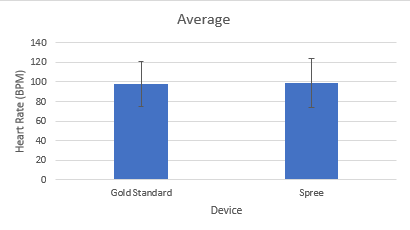
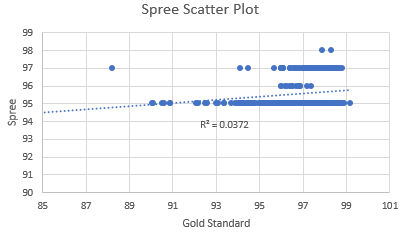
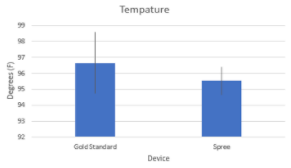
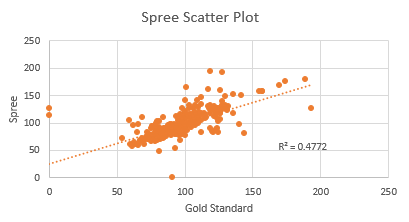
LAB 3 WRITE-UPDescriptive and Inferential Stats and GraphsHeart Rate of Pulse Ox and Spree Gold Standard: Temperature of Gold Standard and Spree Gold Standard: Summary of ResultsHeart Rate of Pulse Ox and Spree Temperature of Oral Thermometer and Spree Design Flaws and RecommendationsBased on the data above, the spree device is not a very specific and adequate way of measuring a person’s temperature and heart rate. One possible design flaw for this experiment is that the trial did not use random sampling. The trial took place on a college campus, therefore, the majority of the people participating would have a healthy heart rate. If the trial used random sampling, there would be people of all ages participating in the trial. Therefore, the data of average heart rate would be significantly more accurate. Another possible design flaw in this experiment would be the use of the oral thermometer. Using an oral thermometer to take a person's temperature is not very accurate. A better alternative for checking the participant's temperature would be through a digital thermometer or an ear thermometer. The digital thermometer uses electronic heat sensors to measure the body's temperature. This is much more precise than an oral thermometer. Using an oral thermometer averages about .5 degrees F to 1.0 degrees F below rectal, ear, and temporal readings, but not only that, but taking oral temperatures after eating or drinking also affect the accuracy of the sample.
"Thermometers: Understand the Options." Mayo Clinic. Mayo Foundation for Medical Education and Research, 12 Sept. 2015. Web. Tousseau, Jennifer. “What Is the Most Accurate Way to Take a Temperature? Is Oral, Temporal, Ear, or Rectal Best?” Systemic Autoinflammatory Disease (SAID) Support, 13 May 2017, saidsupport.org/what-is-the-most-accurate-way-to-take-a-temperature-is-oral-temporal-ear-or-rectal-best/.
Experimental Design of Own DeviceFor the thermal therapy device, multiple temperatures will be taken in order to prove consistency. The goal is for the device to have 95% precision rate in achieving a target temperature. The data will be collected using a separate thermometer, and recorded on an excel sheet. The standard deviation for this experiment is expected to be fairly large (s = due to the fact that it will be both heating and cooling, which would increase the spread between all of the data points. The average value of the data would be larger as well because of the variation in temperature. The correlation of the data would be positive because the temperature goes from low to high and vice versa. In the trial, random sampling would be applied. From every state in the US, two physical therapy offices will be chosen at random and from each of these offices one patient will be chosen to participate in the trial. Having the sample spread out across the country makes the sample fairly representative of the American population that uses heating or cooling pads to treat chronic pain. From every state in the US, two physical therapy offices will be chosen at random and from each of these offices one patient will be chosen to participate in the trial. Thus making the trials more representative of the population, more specifically involving Americans who use heating or cooling pads to treat chronic pain. The participants would use the device for a period of three weeks. In that time, they will record how the temperature of the device feels and what their level of chronic pain is from the beginning to the end of the three weeks. They will rank their pain levels once a day. This way, by the end of the three weeks, they will be able to look back on their progress throughout the trial. | ||||||