BME100 f2017:Group12 W0800 L3
| Home People Lab Write-Up 1 | Lab Write-Up 2 | Lab Write-Up 3 Lab Write-Up 4 | Lab Write-Up 5 | Lab Write-Up 6 Course Logistics For Instructors Photos Wiki Editing Help | ||||||
|
OUR TEAM
LAB 3 WRITE-UPDescriptive Statistics, Inferential Statistics, and Graphs
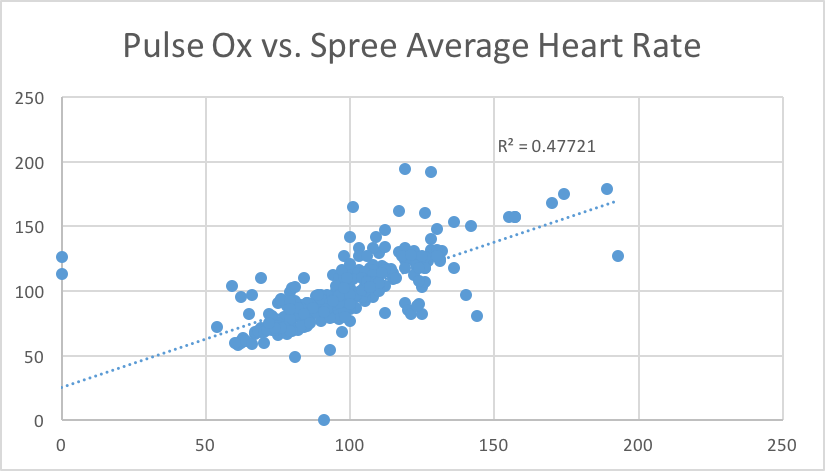
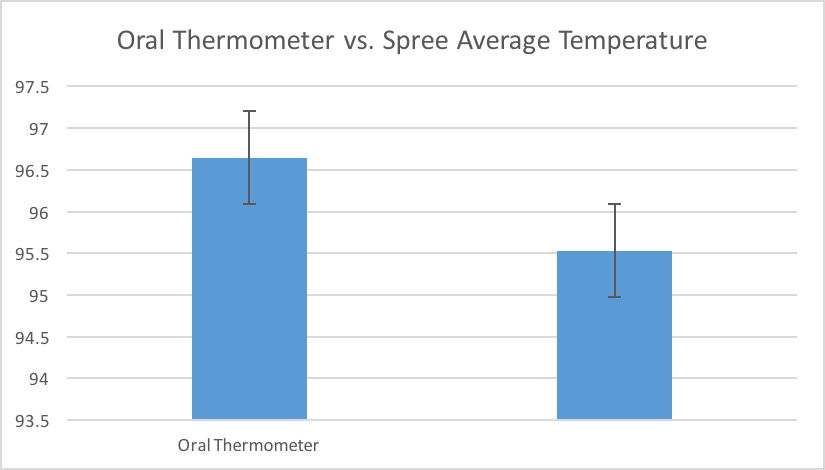
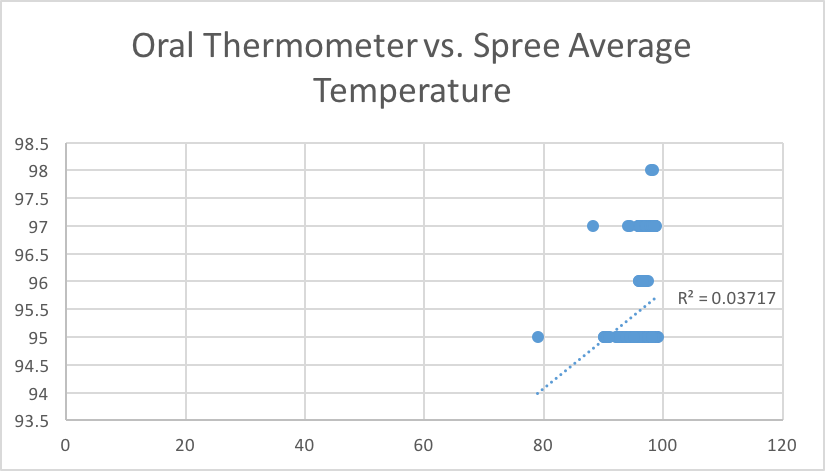
We did the same calculations for temperature as well, this time using an oral thermometer for the gold standard. For the mean of the results from the oral thermometer, we got 96.64716 and for the mean for the Spree, we got 95.530864. The standard deviations were 1.9226021 and .8703783 for the oral thermometer and the Spree headband, respectively. The R coefficient this time was very low at a value of .192798089. This suggests very little correlation between the oral thermometer results and the Spree headband results and this can be verified with our scatter plot. Lastly, our t-test results gave a p value of 1.09676*10^-21. This number is far, far below .05 which is a terrible thing in this experiment as it implies that there is a statistically significant difference between the oral thermometer and the Spree headband. Furthermore, the Spree headband is not good at measuring temperature as it differs too greatly from the gold standard.
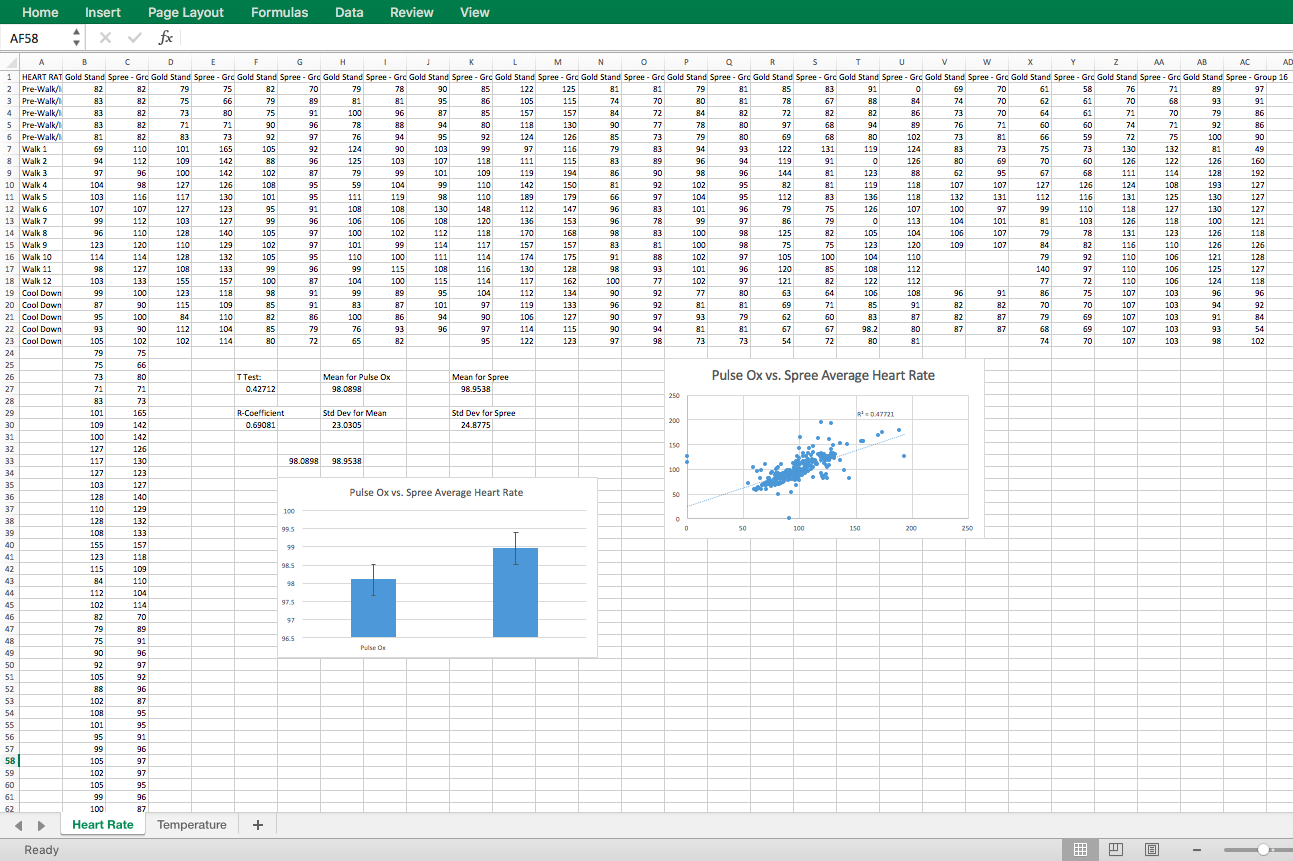
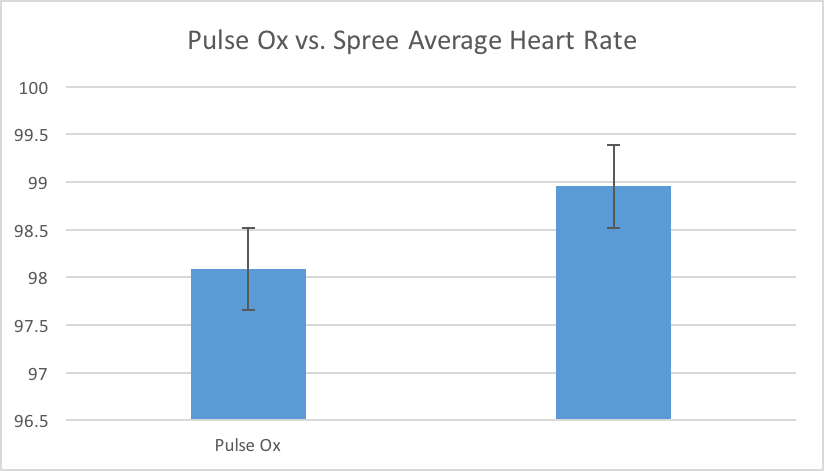
Design Flaws and RecommendationsThe Spree cap that attempts to measure heart rate and body temperature was found to have many flaws in function. While it's measurements for heart rate were found to be semi-accurate, the measurements for temperature, when compared to a gold standard, were found to be very inaccurate. For the heart rate measurements, the semi-accuracy is based off the p value from t-test, and from the Pearson's R constant. According to the p value from the T-Test, the values from heart rate are accurate and connected to the gold standard with statistical significance. But, according to the Persons R value, the measurements did not reach a totally accurate level. The temperature measurements varied between 4 different values (95, 96, 97, and 98 degrees, with extremely frequent readings of 95 degrees) even when the actual readings of the gold standard were very variable and detailed. This is a probable result of a large design flaw in the temperature reading ability of the design. This design flaw must be remedied if the company wishes to market its product as a functional device to measure temperature, and our recommendation is that the designers of the product attempt to approach the problem from a completely new perspective. This is recommended because of the extreme failing of the current measurement process, since its measurements were so significantly statistically different from the gold standards.
Experimental Design of DeviceTo verify that our product reacts specifically to our target bacteria, the stickers will be isolated in three separate chambers without the use of living test subjects contacting the stickers. The independent variable in this procedure will be the presence (or lack thereof) of different airborne bacteria. In one group, the sticker will be contained within a sterile room free from any airborne pathogens; since there is no bacteria to detect, the sticker should ultimately not change color. In a second group, the sticker will be placed in a room where tuberculosis bacteria float freely in the air. The source of the bacteria can come from a living test subject (i.e. a patient infected with tuberculosis) or from a controlled sample obtained from a lab. In this case, the sticker should recognize the proteins of the tuberculosis bacteria and change from colorless to an indicated color. If the product fails to change color during these series of trials, then we would need to return and correct this error before continuing. The third group would involve exposing the sticker to an airborne pathogen that is different from our target bacteria type; in this case, the product would be exposed to pathogens other than the tuberculosis bacterium. Regardless of what other bacteria the mask is exposed to, the mask should not be able to identify the pathogen and change color as it should only be conditioned to react to the tuberculosis bacteria type. The purpose of this group would be to test for false positives. Otherwise, our product would give false readings of the environment and cause unnecessary worry to those who use our sticker. After establishing that the sticker works (efficacy above 0%) and assuming that customers have a reasonable chance of being around TB, we would proceed with conducting a theoretical experiment in regards to comparing our efficacy with existing technology. Our experiment would have three groups: one control group uses blood testing procedures to diagnose themselves, one group uses our competitor’s (Bio-Rad Laboratory) immunofluorescence microorganism identification kit, and one group uses our sticker. The three groups would allow us to compare our sticker against both conventional and contemporary methodology. We would aim for a group size of 40 individuals per group in order to have a sufficient sample size to assume independence even in the case that 25% of our data becomes lost due to experimental error. We would draw our sample from the customer list of Bio-Rad Laboratory, but the selection of the sample would be pseudorandom in order to negate gender, geographical, and social biases. In other words, the sample would not be wholly representative of the population, but rather representative of how our product works on the general population. To get a simple random sample, we would number the customers and then use a random number generator to generate 40 members for the first group, second group, and so forth. We would expect each member of the first and second group to take a survey on how quickly they diagnosed their disease if they had it or why they suspected they had TB. We would want the third group to use their assigned treatment daily and submit a data form weekly. Our measure for the efficacy will be the number of times the patches went off during a day, the number of times they could confirm a TB patient, and the number of times they suspected TB patients. Once we get all the data sets, we would analyze them using ANOVA to see if there was a significant improvement in our identification rates.
| ||||||