BME100 f2016:Group6 W1030AM L3

BME 100 Fall 2016	Home People Lab Write-Up 1 | Lab Write-Up 2 | Lab Write-Up 3 Lab Write-Up 4 | Lab Write-Up 5 | Lab Write-Up 6 Course Logistics For Instructors Photos Wiki Editing Help
OUR TEAM Name: Matt Edick Name:  Edgar Manriquez Name:  D. Brennen Martin Name: Megan O'Reilly Name: Blake Stephens LAB 3 WRITE-UP Descriptive Stats and Graph Temperature: Temp (°F) Gold Standard Spree Average 96.64716049 95.5308642 Standard Deviation 1.922602071 0.870378299 Count 324 324 Standard Error 0.106811226 0.04835435 Heart Rate: Heart Rate (bpm) Gold Standard Spree Average 98.08976898 98.95379538 Standard Deviation 23.03054395 24.87753802 Count 303 303 Standard Error 1.32307018 1.429177217 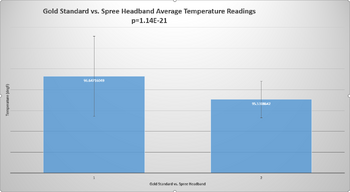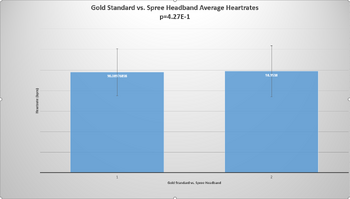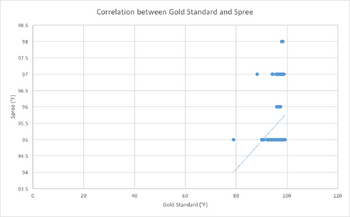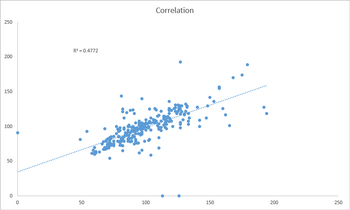Inferential Stats The paired t-test and Pearson's r coefficient were calculated between the gold standard and Spree, for both temperature and heart rate. Temperature: Temp (°F) Data T-Test 1.14066E-21 Pearson's r 0.191688017 Heart Rate: Heart Rate (bpm) Data T-Test 0.427116193 Pearson's r 0.690806489 Design Flaws and Recommendations There were multiple 0 bpm readings recorded for both the gold standard and the Spree headband. Due to the data being from previous classes, it is unknown whether these zeroes were inserted due to missing data or if the machines had errors in their sensors, resulting in a reading of zero. For future research, missing data should be left blank instead of inserting a value of 0 in order to prevent inaccurate statistics being recorded. For temperature in the spree headband there was not much variation as most values came out as 95 degrees where the thermometer came out with more accurate values. Experimental Design of Own Device In order to validate our product, which measures HR, temperature, Blood oxygen levels, and includes a GSR stress sensor, we are looking at a very diverse and large sample size to compare control groups with many changing variables. A control group and changing variable groups are not hard to find given there are 100 Million Americans who suffer of chronic pain and whom we have targeted as our patients. For obvious reasons we won't need to test on all 100 Million persons, but rather a sample size of around 5000 people should give very accurate results for validation on our device. 1000 points in that data set would be held as our control and the other 4000 would be testing the various features of the device versus the golden standard; in this case we would need to compare against the gold standard of each component for best accuracy. The best way to statistically compare the data of the control and the tested is to find little to no difference in the measurements taken by clinically proven devices versus our monitor. Doing this will show how accurate our device is, as well as show how valid our device stands next to proven devices.