BME100 f2016:Group3 W8AM L3
| Home People Lab Write-Up 1 | Lab Write-Up 2 | Lab Write-Up 3 Lab Write-Up 4 | Lab Write-Up 5 | Lab Write-Up 6 Course Logistics For Instructors Photos Wiki Editing Help | |||||||
|
OUR TEAM
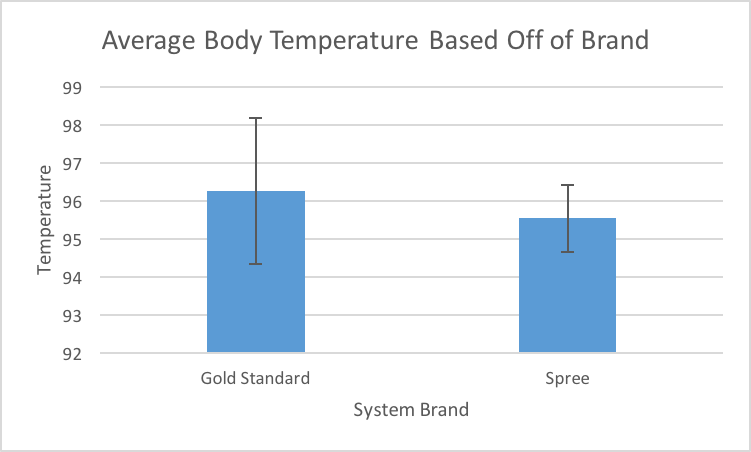
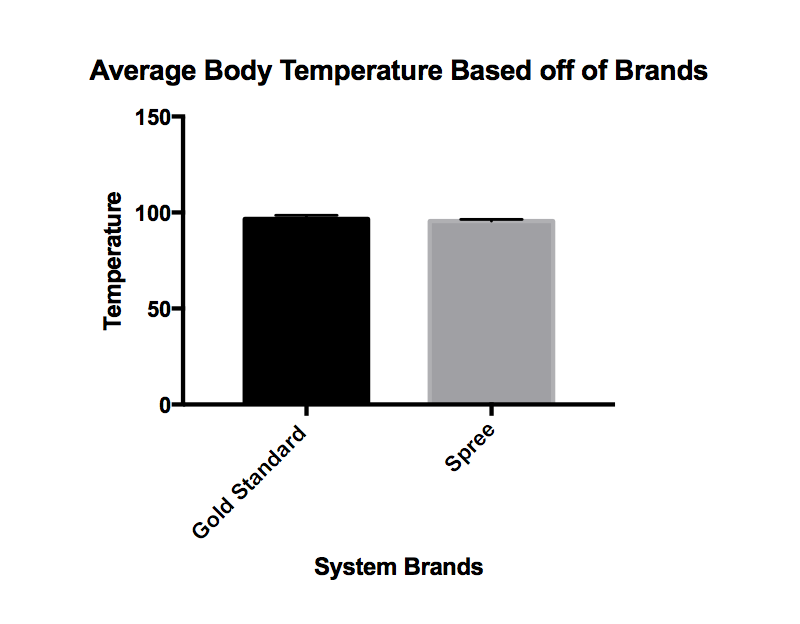
LAB 3 WRITE-UPDescriptive Stats and Graph1) Oral Thermometer Spree Measurements for Temperature:
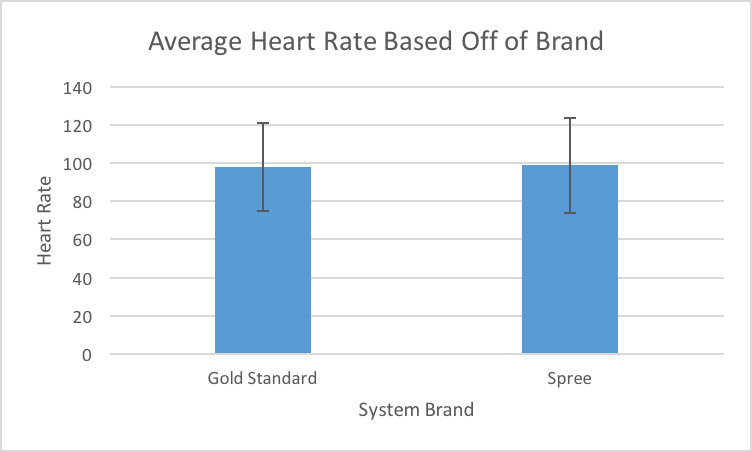
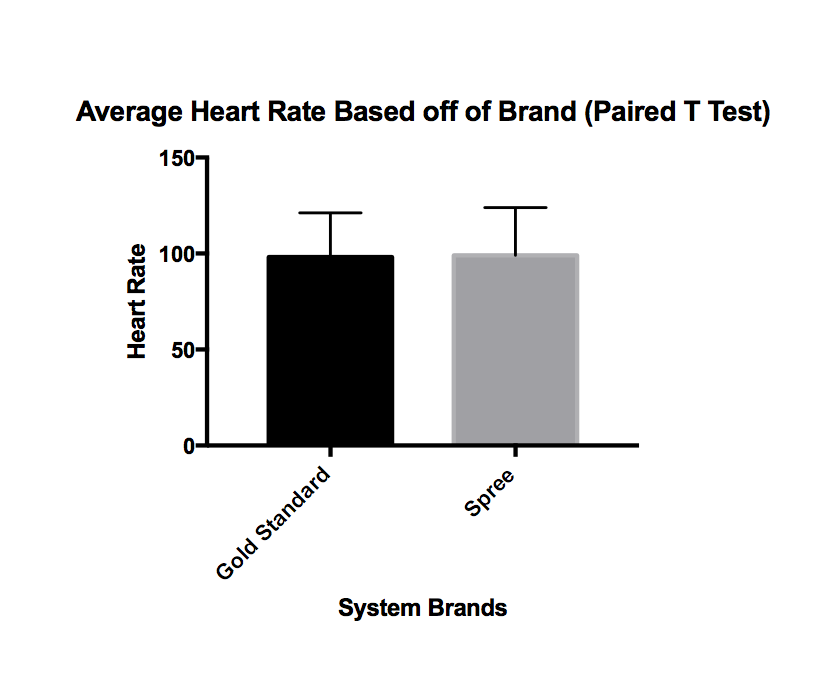
2) Pulse Ox Spree Measurements for Heart Rate
Inferential Stats1) Oral Thermometer and Spree Band Paired T-Test: 2.791*10^-20
T-Test: 0.427116
Design Flaws and RecommendationsBased on the statistical evidence on temperature of the gold standard in comparison to the spree, the paired t-test concludes that the p-value of the experiment for temperature is about zero. Thus, this is less than alpha at 0.05 so we reject the null hypothesis that there is a relationship or equivalence between the data for temperatures for the spree and the Gold Standard. In addition, our correlation coefficient of 0.151 indicates that there is a weak, positive correlation between the temperatures recorded for the spree and the temperatures recorded for the Gold Standard. In conclusion, we can infer that overall the spree does not efficiently provide equivalent measurements of temperature to the Gold Standard. Based on the statistical evidence on heart rate of the gold standard in comparison to the spree, the paired t-test concludes that the p-value of the experiment for heart rate is about 0.427. Since the p-value is greater than alpha at 0.05, we fail to reject the null hypothesis and cannot conclude that there is not a relationship or equivalence between the spree and the Gold Standard in heart rate. In addition, the
Experimental Design of Own DeviceOur group's scientific question is “Does the method in which galantamine is inserted into the body affect how much of the actual drug goes into the bloodstream?” In order to test if our device is valid and safe, our team has decided to put our device through clinical trials. In our experiment, we will have the sample size of 120 patients with Alzheimer's disease. The reason for why we chose 120 patients is because this is our first clinical trial and our team wants to see if it works on a smaller scale, compared to a much bigger one. In our experiment, our independent variable is the form in which the patients receive galantamine, a drug for those suffering from dementia. This drug was created to improve memory, awareness, and the ability to perform daily functions. In this experiment, we will divide the group of 120 people into two groups. Thus, each group will have 60 people. In one group the patients will receive the pill version of galantamine. In the second group, they will have our device implanted in their mouths. Our dependent variable is how much of galantamine goes into the patient's blood system. The control in this experiment is the type of drug used. The suggested amount of galantamine a person uses in the form of a capsule is 16 milligrams. In the device there will be 250 micro-liters of the liquid form of galanatamine in the reservoir.
| |||||||