BME100 f2016:Group13 W1030AM L3
| Home People Lab Write-Up 1 | Lab Write-Up 2 | Lab Write-Up 3 Lab Write-Up 4 | Lab Write-Up 5 | Lab Write-Up 6 Course Logistics For Instructors Photos Wiki Editing Help | |||||||
|
OUR TEAM
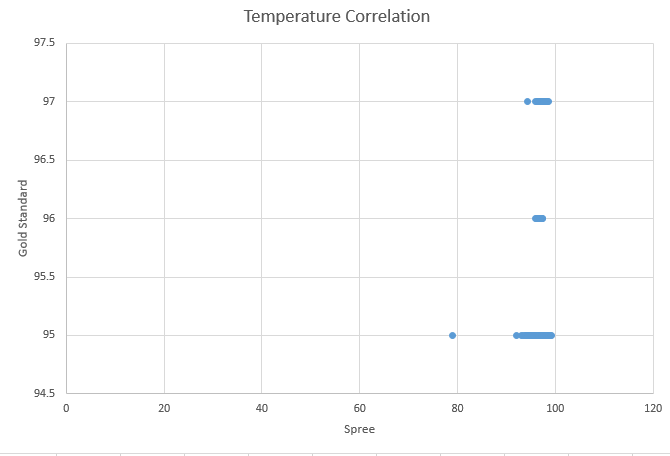
LAB 3 WRITE-UPDescriptive Stats and GraphThe Pearson R value is 0.175577658 showing that there is no correlation between the Gold Standard and Spree tests.
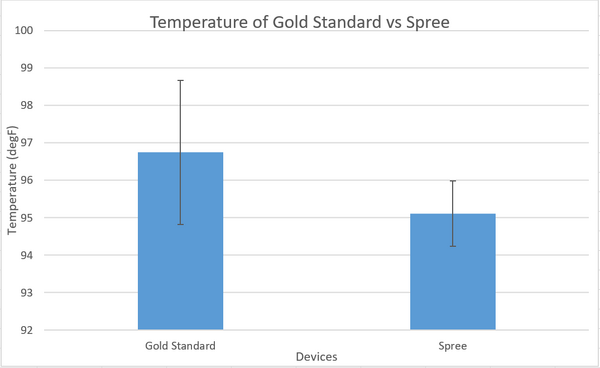
Mean of Gold Standard: 96.7483908 The Pearson R Value is 0.69046 showing that there is a positive correlation between the Gold Standard and Spree tests.
Mean of Gold Standard: 98.19934 Inferential StatsBeats Per Minute
Design Flaws and RecommendationsThe Spree Headband seems exhibits inaccurate temperature readings compared to the Gold Standard. The Spree's accuracy also seems to be lacking in that the band only recorded whole numbers. This lack of correlation with the Gold Standard and overall inaccuracy demands that the band be improved upon in this area. It is recommended that the area of contact can properly determine the body temperature of the wearer and that the technology used is performing as it was designed to perform. On the other hand, our data reflects a positive correlation between the Gold Standard and the Spree when recording the wearers heart beats per minute. Our data reflects and accurate reading of the wearers BPM compared to the Gold Standard. Our data reflected a Person's R of 0.69. This is significant because data reflecting a Pearson's R of 0.5 or greater is considered to be a significant relationship. Since this part of the Spree is recording accurately, the recommendation would be to keep it as is.
Experimental Design of Own DeviceOur experimental design will be extremely extensive because there is no “gold standard” devices for our device. Instead, we are the pioneers in the tremor wristband. Therefore, we will have no other device to compare our device with. In order to ensure accuracy in our device, we will test the patients tremor with and without the wristband. In order to get a sample size that will not bias our data results, we will send out a volunteer trial for individuals that believe they have a severe tremor. This is because our device is going to be used for individuals that only have severe tremors. We will send out the volunteer testing information to assisted livings, physicians, and hospitals. The reason for targeting these groups is because this is where tremors are most prevalent. In order to create incentive for the individuals, we will hold a raffle for all the volunteer subjects in order to win fifty dollars. This will hopefully bring people to our testing and also create a large variety of subjects. Now that we have the subjects, we will have them all come to Arizona State University around five o’clock in order to eliminate the time of the day affecting our results. We will have the subjects and we will make them perform tasks with and without the wristband. For this we will perform a Paired T-Test. The reason for it being a Paired T-Test is because we will be taking two measurements from one group of subjects. One measurement will be the group with the wristband and one without. The tests that we will be performing will be a T-test. The subject will be giving a pencil and a piece of paper with a black line approximately one millimeter in width and eight inches high. The subject will be asked to trace the line without taking the pencil off of the line. The first test, the subject will do this without the wristband. The experimenter will then take a ruler and measure the furthest mark that deviates from the line. This will be measured in millimeters, for the most accurate reading. The subject will do this test five times in a row without the wristband. Then the subject will do the same test with the wristband. The measurements will be calculated. In order to ensure that the subjects fatigue does not affect the results, we will have every other subject switch the order. Therefore, subject one will start without the wristband, but subject two will start with the wristband and so on. We will then perform measurements on central tendency and variability for the group without the wristband and then for the test with the wristband. This will tell us values such as our mean and standard deviations. We will then perform a bar graph. One bar will be the subjects with the wristband and one will be the subjects without the wristband. On the y-axis there will be maximum length, in millimeters, that the subjects drew from the line. Hopefully, we will see that the bar graph for the without wristband will have a higher mean value. We also wish to see the standard deviations being small for each graph. We will then take a T-test to compare the rests of the two groups. The experiment will be a one tailed T-test because we are predicting that the wristband will help the tremor of the subjects. The goal is to get a p value less than .05 so that it is statistically significant. Our null hypothesis would be that there is no relationship between the maximum length of drawing deviation and wearing the wristband.
| |||||||