BME100 f2014:Group30 L3
| Home People Lab Write-Up 1 | Lab Write-Up 2 | Lab Write-Up 3 Lab Write-Up 4 | Lab Write-Up 5 | Lab Write-Up 6 Course Logistics For Instructors Photos Wiki Editing Help | |||||||
|
OUR TEAM
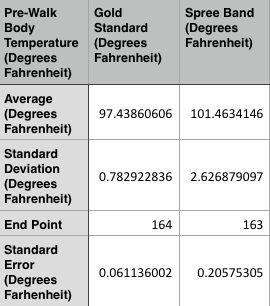
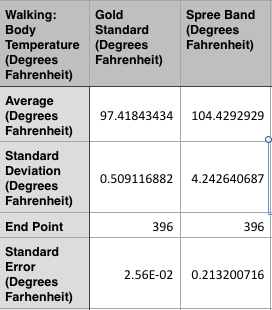
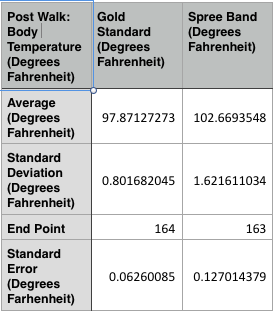
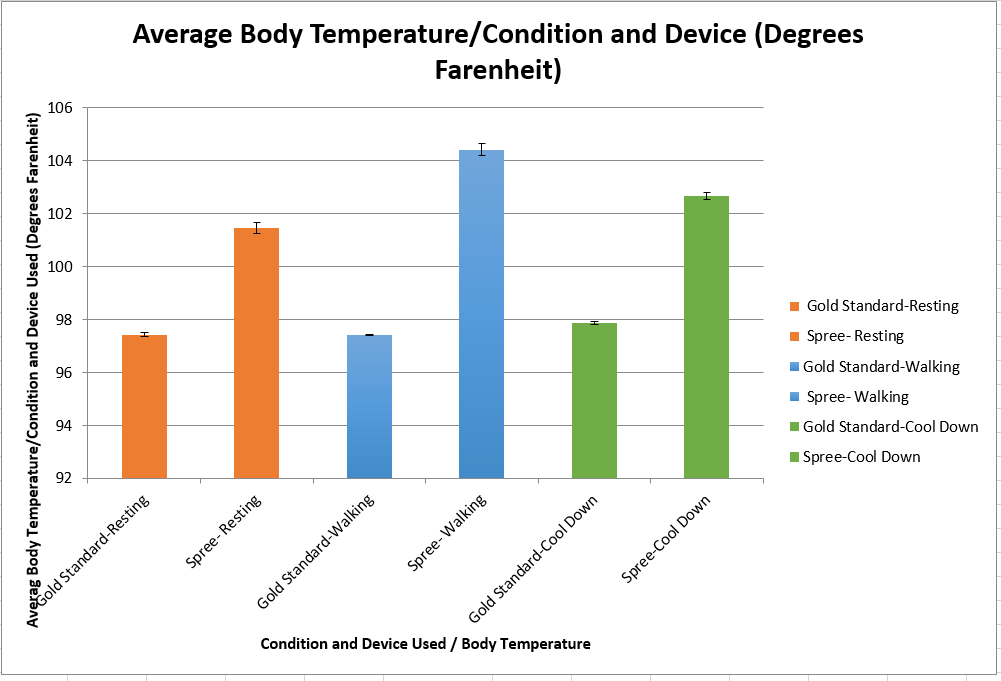
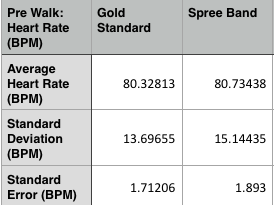
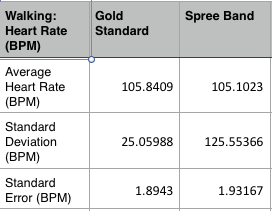
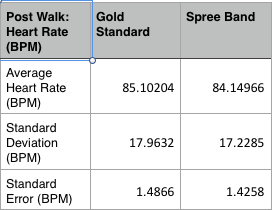
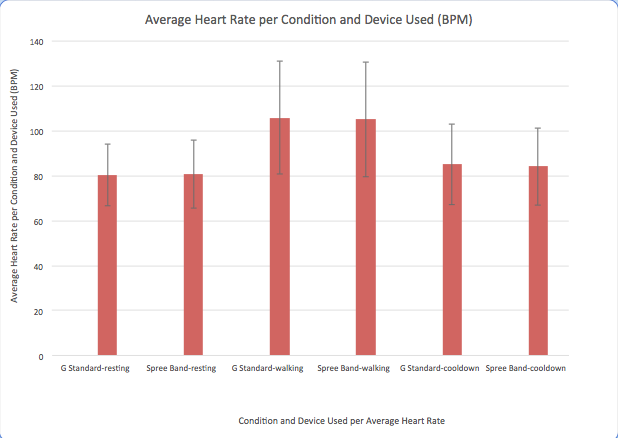
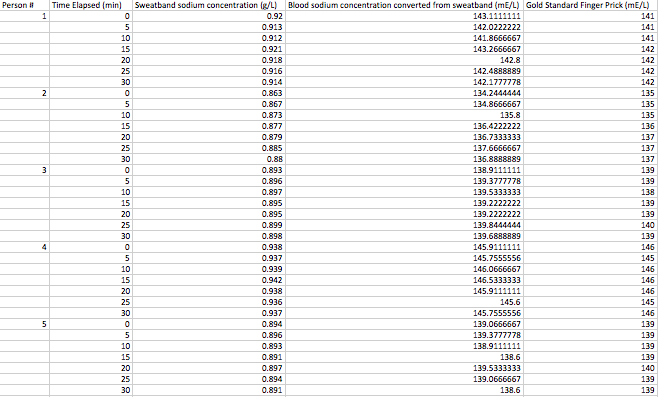
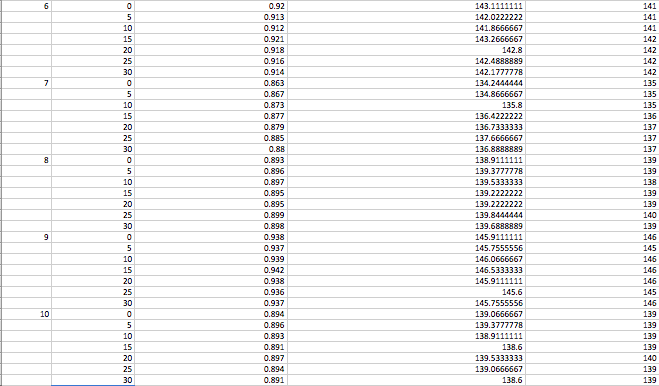
LAB 3A WRITE-UPDescriptive StatisticsBelow is the descriptive data for the body temperature measurements for each condition group and measurement method. Below is a graph comparing mean body temperatures in degrees Fahrenheit for each condition group (average body temperatures before, during, and after walking exercise) and each method of measurement (spree band or gold standard). Below is the descriptive data for the heart rate measurements for each condition group and measurement method.
The means seem to be very similar to each other for all groups, but whether they are significantly different or not will be tested in the inferential statistics.
ResultsAfter performing a t-test, it was found that the p-values for temperature before, during, and after the walk were 5.57*10^-46, 4.4*10^-156, 4.51*10^-64, respectively. The fact that each value is less than the value 0.05 indicates that there is a significant difference between the average body temperatures. These small p-values mean that there is such a significant difference between the spree and the gold standard that there is almost no connection at all between the data values of the two tests. If the nominal values of the spree do in fact mean the body temperature values it says it does, then it clearly doesn't work effectively. As a way to further confirm the relationship between the gold standard device and spree band, the The Pearson's R correlation coefficient was calculated for each condition group. The Pearson's R correlation coefficients for the pre-walk, walking, and post-walk body temperatures were .089, 0.025, and -0.168, respectively. The R values for the pre-walk and walk temperatures groups both indicated a weak positive correlation, while the post-walk body temperature R value indicated a weak negative correlation between the gold standard device and spree device. This means that there are statistically insignificant correlations between the the two devices, and that the spree band is not concurrent with the gold standard device's measurement for body temperature. In regards to heart rate, the p-values were .701029 for the resting group, .47918 for the walking group, and .06193 for the cool down group. Since all of the p-values are greater than .05, the experimenter can be confident that the spree band measures heart rate accurately. The p-values for each of the heart rate group indicate that there is not a statistically significant relationship between the gold standard device and the spree band. Thus, there is evidence that the spree band is concurrent with the gold standard device measurements.
The Pearson's R Coefficient of Correlation for the entire heart rate data set was 0.9079. This means that as a whole, the two methods correspond with or are related to one another. Since there is correlation between the two methods, it is valid to conclude that the spree band is an accurate method to measure heart rate.
AnalysisThe data collected in this experiment clearly displays that the device is inaccurate in comparison to the gold standard for temperature. With P-values that are extremely low, and significantly different standard deviation in both heart rate and temperature, the data does not line up enough for the device to be reliable. The reasoning for these results is that the Spree gives us only four values for temperature, while the thermometer gives us a wide range of temperatures. This causes a lot of variation in the data, resulting in error. The Spree also measures external temperature (skin temperature), while thermometers measure core body temperature.The body is constantly trying to balance temperature through homeostasis, so it is likely that the temperature of the skin is different than the core body temperature. This also results in variation in temperature. Other errors that could have affected the end results of the experiment could be but are not limited to: bluetooth connection issues, human error in taking heart rate by hand, and the thermometer was not stationary while it was taking temperature of the walking subject. As for heart rate, the Pearson's R value shows that the correlation was quite high, all flirting with the value of 90%. This tells us that one could argue that the Spree is relatively reliable for the measurement of heart rate.
Summary/DiscussionWith the Spree band, we concluded that the temperature measurement is very inaccurate. The first reason for error is that the spree measures the temperature and displays it as 4 different levels with a range of values. These values were given degree values to use for analysis, and when using these degree conversions, we concluded that they are very inaccurate when compared to the data that we collected from the gold standard device that we used. Another error with the temperature measurement was the fact that it measures external temperature. This is what caused the inaccurate results because the external temperature is not the same as the internal temperature of the human body. The skin will vary in temperature to try and help maintain the desired internal body temperature, so the Spree band will read an inaccurate measurement.
LAB 3B WRITE-UPTarget Population and NeedThe E-Buddy head band is targeted towards athletes of all ages who have issues with dehydration during athletic performance. Dehydration is a common health issue that is particularly experienced by endurance athletes, as they have the tendency to sweat profusely during workouts thereby losing more water than they take in. This loss of water during exercise can significantly hinder an athlete from performing at their highest performance potential level, since water and electrolytes are needed to maintain homeostasis in the body. Electrolytes (sodium and potassium ions) are needed to stimulate water absorption, which is a key step to staying well-hydrated during exercise. Thus, there is a need for the E-Buddy head band in the athletic world, as the head band will help athletes to stay well-hydrated by monitoring electrolyte levels in their sweat and by notifying them when they should intake more electrolyte-rich fluids.
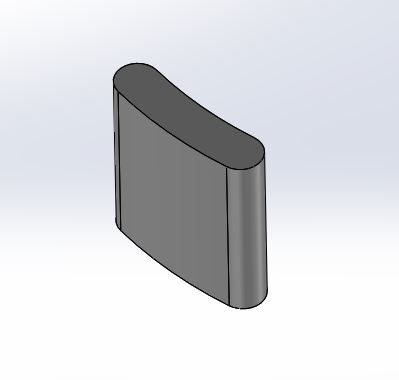
Device DesignHeadband Sensor App
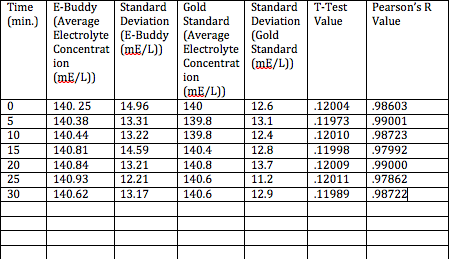
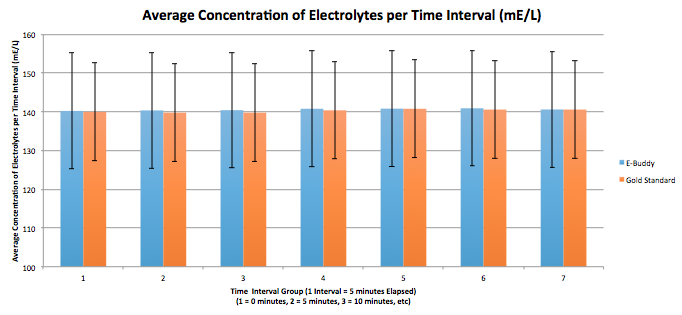
Inferential StatisticsThese inferential statistics display that the device is accurate. The T-test is above .05, which tells us that the change in the data is insignificant. Pearson's R coefficient is above .95, meaning that the data is reliable. GraphThe fact that the standard deviation error bars for each of the compared groups all overlap each other is an indicator that there is no statistically significant difference between each group. Thus, the E-Buddy head band provides an accurate measurement, since there is no statistically significant measurement from the gold standard measurement.
|
|||||||